1.快速排序的描述
快速排序算法采用的分治算法,因此对一个子数组A[p…r]进行快速排序的三个步骤为:
(1)分解:数组A[p…r]被划分为两个(可能为空)子数组A[p…q-1]和A[q+1…r],给定一个枢轴,使得A[p…q-1]中的每个元素小于等于A[q],A[q+1…r]中的每个元素大于等于A[q],q下标是在划分过程中计算得出的。
(2)解决:通过递归调用快速排序,对子数组A[p…q-1]和A[q+1…r]进行排序。
(3)合并:因为两个子数组是就地排序,不需要合并操作,整个数组A[p…r]排序完成。
快速排序的伪代码如下

快速排序的代码如下
//对a[start..end]快速排序
void QuickSort(int a[], int start, int end) {
if (start == end)
return;
//划分后的基准记录的位置,对a[start..end]做划分
int index = Partition(a, start, end);
//int index = PartitionNormal(a, start, end);
//int index = PartionRandom(a, start, end);
if (index > start)
QuickSort(a, start, index - 1); //对左区间递归排序
if (index < end)
QuickSort(a, index + 1, end); //对右区间递归排序
}2 最坏、最佳、一般情况的时间复杂度分析
2.1 Worst-Case 分析
当输入的序列是有序的,或者逆序的时候,即划分的一边一直是没有元素。
此时,快排的算法效率递归式以及递归树如下图所示,显然时间复杂度为Θ(n^2)。
2.2 Best-Case 分析
快排划分的最佳情况为,Partition每次分划的时候正好将数组划分成了两个相等的子数组。
递归式为: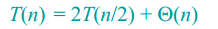
时间复杂度为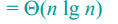
另一种情况为数组被划分为两个长度不等的子数组,比如两个子数组划分的比例是1:9。
这时,递归式为: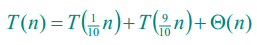
递归树为:
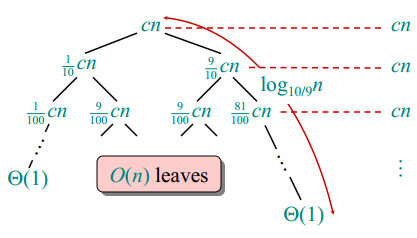
显然,树的最低高度为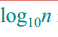
树的最高高度为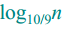
因此,时间复杂度的范围为: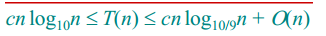
综上所述,可以知道快排在最佳情况下的算法效率是Θ(nlgn)。
2.3 最佳和最差循环交替情况分析
上面我们分析了最好与最坏情况下的算法效率,那么更加普遍的情况是,当最坏情况与最优情况同时都有出现时的算法效率呢?我们假设算法中最坏与最优情况交替出现,那么算法的效率分析如下所示。
最佳情况时,递归式为: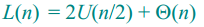
最差情况时,递归式为: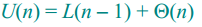
最差递归式代入最佳递归式得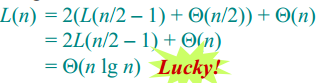
仍然是最佳情况时的时间复杂度。
一般情况下已第一个元素作为Partition的基准元素的代码如下所示:
//普通划分,已数组第一个元素作为基准元素
int PartitionNormal(int a[], int low, int high) {
int pivot = a[low];
int i = low - 1;
for (int j = low + 1; j <= high; j++) {
if (a[j] <= pivot) {
i++;
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
a[i + 1] = pivot;
return i + 1;
}3 随机化快速排序
我们已经知道,若输入本身已被排序,那么对于快排来说就糟了。那么如何避免这样的情况?
两种解决方案:
1:随机排列序列中的元素;
2:随机地选择基准元素(pivot);
这便是随机化快速排序的思想,这种快排的好处是:其运行时间不依赖于输入序列的顺序。
这里使用第二种方法:随机选择基准元素。如下图所示是随机化快速排序的递归表达式。
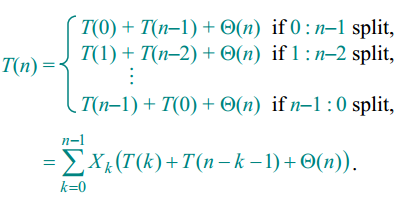
随机化快速排序的Partition代码如下所示:
//产生一个 [low,high]之间的随机数
int GenerateRandomNum(int low, int high) {
if (low < high)
return rand() % (high - low + 1) + low;
else
return low;
}
void Swap(int& a, int& b) {
int t = a;
a = b;
b = t;
}
//随机化划分,随机选择数组中的数作为基准元素
int RandomPartitionEnd(int a[],int low,int high) {
if (low == high)
return low;
int index = GenerateRandomNum(low, high);
int pivot = a[index];
Swap(a[index],a[high]);
int i = low-1;
for(int j=low;j<high;j++) {
if(a[j]<=pivot) {
Swap(a[i+1],a[j]);
}
}
Swap(a[i+1],a[high]);
return i+1;
}附随机化快速排序的时间复杂度具体证明以及分析如下,我表示这里证明起来很麻烦啊(⊙︿⊙)(⊙︿⊙),这里用到一个重要的工具,那就是指示器随机变量,它为概率与期望之间的转换提供了一个便利的方法,这里给出指示器随机变量I{A}的定义。
给定一个样本空间S和事件A,那么事件A对应的指示器随机变量I{A}定义为

下面介绍随机化版本的快速排序算法,时间复杂度T(n)期望的求解和证明。
1.设指示器随机变量

2.随机化后T(n)可能的取值

3.计算随机化后T(n)的数学期望,这里用到了一个非常机智的技巧,就是使用指示器随机变量将随机化后的T(n)用数学公式归纳出来。如何将指示器随机变量与随机化后的T(n)联系到一起,是证明的关键。
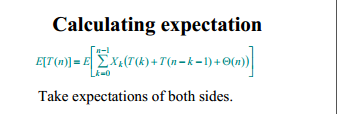
4.计算

5.证明T(n)期望的时间复杂度,这里显然要使用代换法,并且使用了一定的数学技巧求期望的和。


最后
以上就是鲜艳雨最近收集整理的关于MIT算法导论-第四讲-快速排序1.快速排序的描述2 最坏、最佳、一般情况的时间复杂度分析3 随机化快速排序的全部内容,更多相关MIT算法导论-第四讲-快速排序1.快速排序的描述2内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。









发表评论 取消回复