概述
图的存储结构、图的搜索方式、路径
涉及算法：BFS、DFS、Dijkstra
应用领域：区块链、网络
背景知识：
图的概念（节点与节点的映射关系，有向-无向），边是顶点对，不考虑重边和自回路。
图的存储结构， 1.邻接矩阵 G[N][N] （适于稠密图） 2.邻接表 G[N] 为指针数组，对应矩阵每行一个链表，只存非0元素 （适于稀疏图）。
DFS 算法思想，从树的根节点出发，一直往下找它的子节点，找到最深的节点后返回上一节点寻找它的除了刚才深入的子节点以外的子节点，当全部节点遍历一遍后，一直返回，返回至最初根节点。（用递归调用的方式+堆栈）
//DFS伪代码
void DFS （Vertex v）//容器v
{ visited[v]=true;//初始时v没有被访问过,true为标记已访问
for（v的每个邻接点w）{//每个未访问过的邻接点对他的邻接点又进行下一次的访问，取容器v中的数据
if（!visited[w]）DFS(w);}
}
void listcomponents（Graph G）//对图中某组成部分的的打印
{ for（each V in G）
If（！visited[v]）{DFS(v);}
}
BFS 算法思想，从树的根节点开始，找到属于这个根节点的所有子节点，按照一定规则再去选择一个节点作为接下来的根节点，相当于每次的访问是一个根节点的范围。（用递归调用的方式+队列）
//BFS 伪代码
void BFS（Vertex v）
{ visited[v]=true;
Enqueue(v,Q)//将v节点压入队列
while（！IsEmpty(Q)）//队列为空时跳出
{ v=Dequeue(Q);
for（v的每个邻接点w）{//每个未访问过的邻接点对他的邻接点又进行下一次的访问，此时邻接点
//取为队列Q中进入的邻接点一个个去访问
{ if(!visited[w])
{visited[w]=true;Enqueue(w,Q);}
}
}
常见问题：路径规划问题
首先谈下有权单源最短路问题（无判负环）
Dijstra算法
1.令s={源点s+已经确定的最短路径的顶点vi}
2.对任一未收录的顶点v，定义dist[v]为s到v的最短路径长度，但该路径仅经过s中的顶点。
即路径{s->(vi∈s)->v}的最小长度。每次从未收录的顶点中选一个dist最小的收录（贪心思想）
void Dijkstra (vertex s)
{
while(1){
v=未收录顶点中dist最小者;
if(这样的v不存在) break;
collect[v]=true;
for(v的每个邻接点w){
if（collected[w]==false）
{ if(dist[v]+E<v,w> < dist[w]) {
dist[w]=dist[v]+E<v,w>;
path[w]=v;
}
}
}
}
例题：POJ1062
题目描述 Description
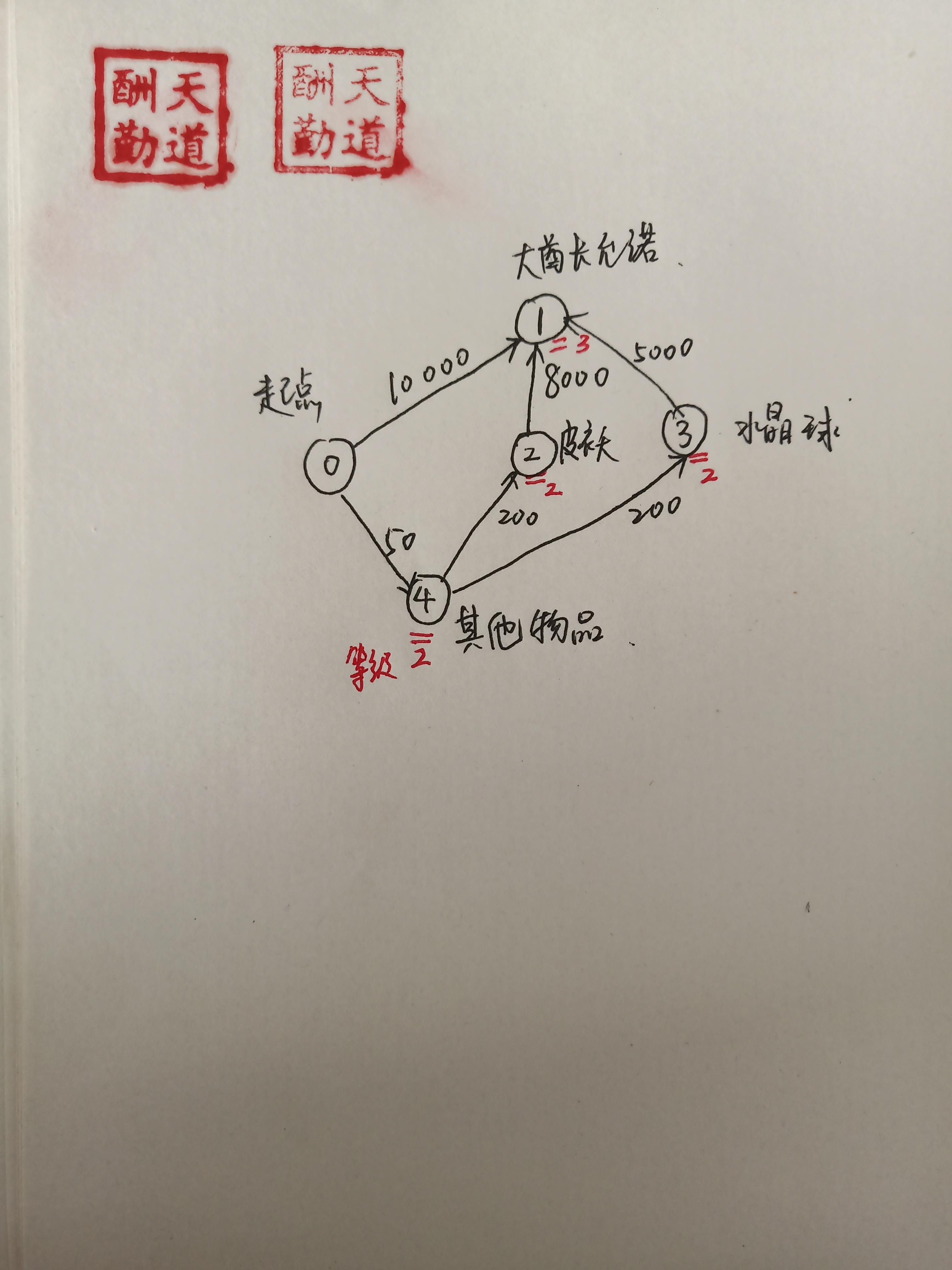
年轻的探险家来到了一个印第安部落里。在那里他和酋长的女儿相爱了，于是便向酋长去求亲。酋长要他用10000个金币作为聘礼才答应把女儿嫁给他。探险家拿不出这么多金币，便请求酋长降低要求。酋长说：“嗯，如果你能够替我弄到大祭司的皮袄，我可以只要8000金币。如果你能够弄来他的水晶球，那么只要5000金币就行了。”探险家就跑到大祭司那里，向他要求皮袄或水晶球，大祭司要他用金币来换，或者替他弄来其他的东西，他可以降低价格。探险家于是又跑到其他地方，其他人也提出了类似的要求，或者直接用金币换，或者找到其他东西就可以降低价格。不过探险家没必要用多样东西去换一样东西，因为不会得到更低的价格。探险家现在很需要你的帮忙，让他用最少的金币娶到自己的心上人。另外他要告诉你的是，在这个部落里，等级观念十分森严。地位差距超过一定限制的两个人之间不会进行任何形式的直接接触，包括交易。他是一个外来人，所以可以不受这些限制。但是如果他和某个地位较低的人进行了交易，地位较高的的人不会再和他交易，他们认为这样等于是间接接触，反过来也一样。因此你需要在考虑所有的情况以后给他提供一个最好的方案。为了方便起见，我们把所有的物品从1开始进行编号，酋长的允诺也看作一个物品，并且编号总是1。每个物品都有对应的价格P，主人的地位等级L，以及一系列的替代品Ti和该替代品所对应的“优惠”Vi。如果两人地位等级差距超过了M，就不能“间接交易”。你必须根据这些数据来计算出探险家最少需要多少金币才能娶到酋长的女儿。
输入描述 Input Description
输入包括了多个测试数据。每个测试数据的第一行是两个整数M，N（1<=N<=100），依次表示地位等级差距限制和物品的总数。接下来按照编号从小到大依次给出了N个物品的描述。每个物品的描述开头是三个非负整数P、L、X（X<N），依次表示该物品的价格、主人的地位等级和替代品总数。接下来X行每行包括两个整数T和V，分别表示替代品的编号和“优惠价格”。
输出描述 Output Description
对于每个测试数据，在单独一行内输出最少需要的金币数。
样例输入 Sample Input
1 4
10000 3 2 //酋长的允诺
2 8000
3 5000
1000 2 1 //大祭司的皮袄
4 200
3000 2 1 //大祭司的水晶球
4 200
50 2 0 // 其他某件物品
样例输出 Sample Output
5250
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#define MAXN 1010
#define INF 0x3f3f3f3f //借鉴了博主 ametake的用法
using namespace std;
int map[MAXN][MAXN],dis[MAXN],vis[MAXN],cost[MAXN],level[MAXN],can_change[MAXN];
int n,m;
void init()
{
for (int i = 1;i <= n;i++)
{
for (int j = 1;j <= n;j++)
{
if (i != j) map[i][j] = INF;
else map[i][j]= 0;
}
}
}
int dijkstra()
{
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
dis[1]=0;int pos;
for(int i=1;i<=n;i++)
{
int mindj=INF;
for(int j=1;j<=n;j++)
{
if(dis[j]<mindj&&!vis[j]&&can_change[j])
{
mindj=dis[j];
pos=j;
}
}
vis[pos]=1;
for(int j=1;j<=n;j++)
{
if(can_change[j])
{
dis[j]=min(dis[j],dis[pos]+map[pos][j]);
}
}
}
int ans=INF;
for(int i=1;i<=n;i++)
{
dis[i]+=cost[i];
ans=min(ans,dis[i]);
}
return ans;
}
int main ()
{
while(cin>>m>>n)
{
init();
int x,t,c;
for(int i=1;i<=n;i++)
{
cin>>cost[i]>>level[i]>>x;
for(int j=1;j<=x;j++) //建图
{
cin>>t>>c;
map[i][t]=c;
}
}
int king_level=level[1];
int ans=INF;
for(int i=0;i<=m;i++)
{
memset(can_change,0,sizeof(can_change));
for(int j=1;j<=n;j++) //每次dijkstra的边界条件
{
if(level[j]>=king_level-m+i&&level[j]<=king_level+i)
can_change[j]=1;
}
ans = min(ans,dijkstra());
}
cout<<ans<<endl;
}
return 0;
}
此类问题就是考察思维转化的能力，在了解dijkstra算法后，明确看到题目中的限制边界条件。
限于篇幅有限，最小生成树、kruskal、AOV、AOE等的算法不在放入此内详细讲解。
参考文献：
CSDN博主fengzhizi76506 ：https://blog.csdn.net/fengzhizi76506/article/details/98758958
CSDN博主「ametake」：https://blog.csdn.net/ametake/article/details/45396965
MOOC 陈越/何钦铭 《数据结构》
MOOC 郭炜《程序设计与算法》
最后
以上就是天真音响为你收集整理的BFS、DFS、Dijkstra （POJ1062）的全部内容，希望文章能够帮你解决BFS、DFS、Dijkstra （POJ1062）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复