一、直接插入排序
数据结构的排序方法,常见的有:直接插入排序、冒泡排序、快速排序、直接选择排序,这里只讲解 直接插入排序 是怎么实现的。
1.1、基本思想是这样的
有一个数组R,将数组R分为两个子区间:R[1 … i-1] 和 R[i … n],索引从1开始,n是数组长度( R[0] 另有作用)。前一个子区间 R[1 … i-1] 是有序区,一开始只有 R[1] 一个元素,而无序区是 R[2 … n] 。在排序过程中,需要每次从无序区取出 第一个 元素,把它插入到有序区的适当位置,形成新的有序区。经过 n-1 次插入后,无序区为空,有序区包含了数组R的全部 n 个元素,至此排序完毕。
举个栗子,我们假定有数组:R[46, 39, 17, 23, 28, 55, 18, 46]
那么在初始状态(即 i=1 时),有序区只有 R[1] 即 46 这一个元素,而此时的数组图解如下:

1.2、直接插入排序的算法描述
void InsertSort(SeqList R,int n){
int i,j;
for(i=2; i<=n; i++){
if(R[i].key < R[i-1].key){
R[0] = R[i];
for(j=i-1; R[0].key<R[j].key; j--){
R[j+1] = R[j];
}
R[j+1] = R[0];
}
}
}
1.3、详细解释 i=2 时的直接排序过程
初始状态(i=1)下,有序区只有元素 R[1] 即 46 ,下面详细走一遍 i=2 时的直接排序过程:
//i=2时,R[i].key即为R[2]的值:39,
//R[i-1].key即为R[1]的值:46
if(R[i].key < R[i-1].key){//39<46,满足条件,继续执行
R[0] = R[i];
//将R[i]即R[2]赋值给R[0],所以R[0]的值为39。注意R[0]不指向46,它充当元素交换位置时的桥梁,并在后续代码中检查有序区是否出现索引越界(j=0)
//下面代码解决问题:无序区第一个元素如何适当插入有序区中
//i=2时,j=1,R[0].key即元素39,R[j].key即R[1]的值:46
//判断是否满足条件:R[0].key<R[j].key
for(j=i-1; R[0].key<R[j].key; j--){
//39<46,条件满足,继续执行
R[j+1] = R[j];
//将元素R[j]即R[1]的值 赋给R[j+1]即R[2],此时的有序区元素位置是这样的:R[1]是元素46,R[2]是元素46
//继续执行代码:j--;
//得到j=0,而此时不满足条件R[0].key<R[j].key,结束for循环
}
R[j+1] = R[0];
//上面代码执行时,j=0,所以R[0]的值赋给了R[1],即有序区元素位置:R[1]是元素39,R[2]是元素36,无序区元素位置:R[3]元素17,R[4]元素23,R[5]元素28,R[6]元素55,R[7]元素18,R[8]元素46。
}
i=2时,排序结果图解:有序区有元素 39、46 ,无序区有元素 17、23、28、55、18、46

1.4、详细解释 i=3 时的直接排序过程
//i=3时,R[i].key是R[3]的值17,
//R[i-1].key是R[2]的值46
//条件R[i].key < R[i-1].key满足:17<46
if(R[i].key < R[i-1].key){
R[0] = R[i];
//将R[i]赋给R[0],所以R[0]的值是17
//下面代码解决问题:无序区第一个元素如何适当插入有序区中
//i=3时,j=2,R[0].key是17,R[j].key即R[2]的值46
//判断是否满足条件R[0].key<R[j].key
for(j=i-1; R[0].key<R[j].key; j--){
//17<46,条件满足,继续执行
R[j+1] = R[j];
//将R[j]即R[2]的值46 赋给R[j+1]即R[3],此时的有序区元素从1到3分别是39,46,46
//继续执行代码:j--;
//得到j=1,R[0].key是17,R[j].key即是R[1]的值39
//满足条件:17<39,继续下一个循环
//执行代码:R[j+1] = R[j];
//将R[j]即R[1]的值39 赋给R[j+1]即R[2],此时的有序区元素从1到3分别是39,39,46
//执行代码:j--;
//得到j=0,条件R[0].key<R[j].key不满足,结束循环
}
R[j+1] = R[0];
//上面代码执行时,j=0,所以R[0]的值赋给了R[1],即此时有序区元素从1到3分别为17,39,46
}
i=3时,排序结果图解:有序区有元素 17、39、46 ,无序区有元素 23、28、55、18、46
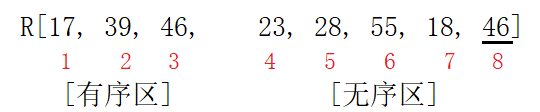
后面 i=4、5、6、7、8的就不一一演示了。
1.5、总结
直接插入排序的思想简单来说就是:先人为的给数组 R 分出两个子区间:有序区和无序区;有序区一开始只有一个元素R[1],然后我们遍历数组 R 除R[1]以外的值,即遍历无序区的值,这就是第一个 for 循环。每次遍历都把无序区的第一个元素R [i] 拿出来放在 R[0] ,然后将 R[0] 和有序区的元素 R[j] 从最后一位到第一位挨个做比较,这是第二个 for 循环,满足条件则 R[0] 占据 R[j] 的位置,R[j] 往后移一位,不满足条件 R[j] 不移位。
第一个 for 循环是找到无序区的第一个元素,第二个 for 循环是从最后一位到第一位依次遍历有序区,将无序区的第一个元素依次与有序区元素比较,满足条件则插入有序区,不满足则结束循环,继续第一个 for 循环,直到第一个 for 循环结束。
直接插入排序时间复杂度:平均情况是O(n2),最好情况下是O(n),最坏情况下是O(n2),空间复杂度O(1);直接插入排序是稳定的。
二、二分查找
对表来说,有三种查找方法:顺序查找、二分查找、分块查找。顺序查找就是遍历表,依次比较表中的值是不是要查找的值 k 。
2.1、二分查找过程
二分查找呢,首先要求被查找的表是一个排好了顺序的表,所以我们拿到的表不一定是排好序了的,那么这就至少需要 O(nlong2n) 的时间进行排序得到有序表 R[1 … n] 。比较的过程是将待查值 k 与有序表的中间位置mid 上的值进行比较,如果 k==R[mid].key,则查找成功,返回 下标mid ;如果 k<R[mid].key ,则 k 在左子表 R[1 … mid-1] 中,需要在左子表中进行二分查找;如果 k>R[mid].key ,则说明 k 在右子表 R[mid+1 … n] 中,需要在右子表中进行二分查找。
2.2、二分查找算法解释
二分查找的过程是递归的,算法描述如下:
int BinSearch(SEQList R, KeyType k, int low, int high){
int mid;
//表R的中间位置是mid
if(low <= high){
//如果被查找子表的最低位置<=最高位置,即确定被查找的子表范围
mid = (low+high)/2;
//确定被查找子表的中间位置
if(k==R[mid].key) return mid;
//如果中间位置的值等于待查值,返回中间位置mid(返回下标mid)
if(k<R[mid].key) return BinSearch(R, k, low, mid-1);
//如果待查值小于中间位置值,则继续在左子表中查找
else return BinSearch(R, k, mid+1, high);
//如果待查值大于中间位置值,则继续在右子表中查找
}
}
2.3、总结
所以说二分查找的“二分”,就是每次查找都将 被查找表 分作了两份,待查值 k 要么是表的中间值,要么在左子表中,要么在右子表中。
最后
以上就是调皮鞋垫最近收集整理的关于直接插入排序是怎么实现的 & 二分查找总结的全部内容,更多相关直接插入排序是怎么实现的内容请搜索靠谱客的其他文章。








发表评论 取消回复