几种简单的插值方法与实例

          插值方法及MATLAB实例解析

插值：已知有限个已知数据点，求得的插值函数必须过这些点，然后在这个范围内用插值函数求得未知数据点的值。

拟合：已知有限个已知数据点，但拟合函数不用过每一个数据点，只要在这些点的总偏差最小。

下面的几种插值方法不再赘述，可以参考链接，具体的会在程序中注解。

1. 分段线性插值
   参考资料
2. 样条插值
   方法描述
3. 拉格朗日插值多项式
   拉格朗日插值的基函数为：
   $$l_i=\frac{(x-x_0)\cdot \cdot \cdot (x-x_{i-1})(x-x_{i+1})\cdot \cdot \cdot (x-x_n)}{(x_i-x_0)\cdot \cdot \cdot (x_i-x_{i-1})(x_i-x_{i+1})\cdot \cdot \cdot (x_i-x_n)}$$
             $={\prod }_{(j=0,j\ne i)}^n\frac{x-x_j}{x_i-x_j},i=0,1,...,n。$
   
   拉格朗日基函数经过每一个已知点。
   $l_i$是n次多项式，满足：
   $$l_i(x_i)=\{\begin{array}{cc}0,j\ne i,& \\ 1,j=i。& \end{array}$$
   拉格朗日插值函数：
   $$L_n(x)=\sum _{i=0}^n{y}_i{l}_i(x)=\sum _{i=0}^n{y}_i(\prod _{i=0}^n)\frac{x-x_j}{x_i-x_j}。$$

举个简单的例子：
已知三个点$(x_1,y_1),(x_2,y_2),(x_3,y_3)，x_1\ne x_2\ne x_3$,那么拉格朗日插值函数就可以写成：

$f(x)=y_1\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+y_2\frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+y_3\frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)}$

不难发现：当$x=x_1,x_2,x_3$的时候，刚好是已知点对应的函数值，要插值的时候只需将$x$换成该范围内的任意值即可，这下你应该很清楚了。

4. 例题与程序

%插值
clear,clc
x0=[0   3   5   7   9   11   12   13   14  15];       %已知数据点
y0=[0  1.2  1.7  2.0  2.1  2.0  1.8  1.2   1.0  1.6];
x=0:0.1:15;                   %要插值的点 
y1=interp1(x0,y0,x);          %第一种插值法：默认线性插值（分段线性插值）

y2=interp1(x0,y0,x,'spline'); %第二种插值法：三次样条插值
                              %csape(x0,y0,conds)
pp1=csape(x0,y0);             %csape()函数返回给定点（x0,y0）的三次样条插值，此处conds默认为complete
y3=ppval(pp1,x);              %ppval函数给出三次样条插值pp在x处对应的函数值

pp2=csape(x0,y0,'second');   %此处conds为边界为二阶导数，默认值为[0 0]
y4=ppval(pp2,x);
%y3和y4的差别在于conds的选择不同


%拉格朗日插值
syms t;
sum=0;
f=1;
for i=1:10
    for j=1:10
        if j==i
            continue;   %i=j时跳出本次循环
        else
        f=f.*(((t-x0(j))./(x0(i)-x0(j))));    %基函数表达式
        end
    end
    sum=sum+f.*y0(i);    
    f=1;
end
y5=vpa(subs(sum,t,x),6)            %将符号变量替换为x

A=[x',y1',y2',y3',y4',y5'];        %输出5种插值点的函数值
vpa(A,6)                           %显示5位有效数字


%-------------------------------绘图-----------------------------%
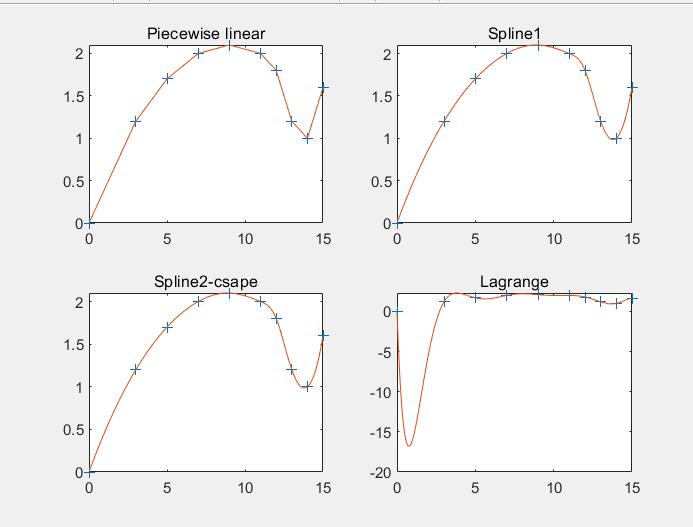
subplot(2,2,1)
plot(x0,y0,'+',x,y1,'-')     %绘制原来数据点和分段线性插值的图像
title('Piecewise linear')

subplot(2,2,2)               %用spline插值
plot(x0,y0,'+',x,y2)
title('Spline1')

subplot(2,2,3)               %用csape插值 
plot(x0,y0,'+',x,y3)
title('Spline2-csape')

subplot(2,2,4)               %用拉格朗日插值 
plot(x0,y0,'+',x,y5)
title('Lagrange')

%求x=0处的曲线斜率
dx=diff(x);
dy=diff(y3);
dy_dx=dy./dx;
dy_dx0=dy_dx(1)       

%求x<=13<=15内的最小点
ytemp=y3(131:151);        %步长是0.1
ymin=min(ytemp);          %找到y的最小的y值再找到对应的x值
index=find(y3==ymin);     %find()函数，返回.....的索引
xmin=x(index);
min_point_13_15=[xmin,ymin]   

结果如下:

最后

以上就是忧虑白云为你收集整理的几种简单的插值方法与实例的全部内容，希望文章能够帮你解决几种简单的插值方法与实例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。