一、插入类排序.
二、交换类排序.
三、选择类排序.
四、归并类排序.
五、基数排序.
注:按关键字非递减排序(从小到大排序)。
目录
- 1、直接插入排序
- 1.1、思想与代码实现
- 1.2、排序的时间分析
- 2、折半插入排序
- 2.1、思想与代码实现
- 2.2、排序的时间分析
- 3、表插入排序
- 3.1、思想与代码实现
- 3.2、排序的时间分析
- 4、希尔排序(缩小增量排序)
- 4.1、思想与代码实现
- 4.2、排序的时间分析
- 后记
内部排序的过程是一个逐步扩大记录的有序序列长度的过程。
插入类排序:将无序子序列中的一个或几个记录“插入”到有序子序列中,从而增加记录的有序子序列的长度。
1、直接插入排序
1.1、思想与代码实现
将一个记录插入到已排好序的有序表中,从而得到一个新的、记录数增1的有序表。
排序过程:
整个排序过程为 n-1 趟插入,即先将序列中第1个记录看成是一个有序子序列,然后从第2个记录开始,逐个进行插入,直至整个序列有序。
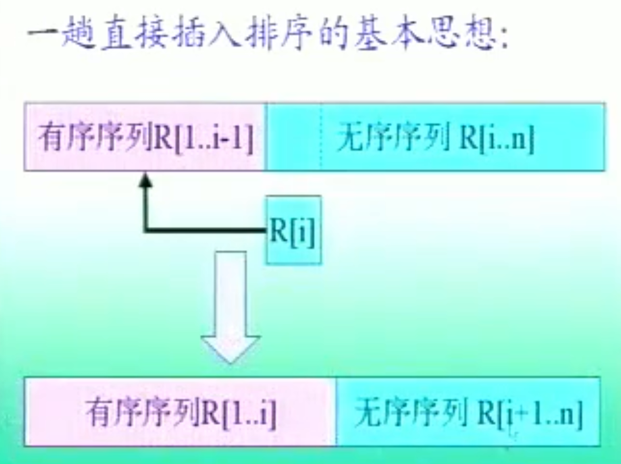
实现 “一趟插入排序” 可分为三步进行:
1、在 R[1 .. (i-1)] textbf{R[1 .. (i-1)]} R[1 .. (i-1)] 中查找 R[i] textbf{R[i]} R[i] 的插入位置: R[1..j] ⩽ R[i] < R[(j+1)..(i-1)] textbf{R[1..j]} leqslant textbf{R[i]} < textbf{R[(j+1)..(i-1)]} R[1..j]⩽R[i]<R[(j+1)..(i-1)];
2、将 R[(j+1)..(i-1)] textbf{R[(j+1)..(i-1)]} R[(j+1)..(i-1)] 中的所有记录均后移一个位置;
3、将 R[i] textbf{R[i]} R[i] 复制到 R[j+1] textbf{R[j+1]} R[j+1] 的位置上;
#define MAX_SIZE 20 //定义顺序表的最大长度
typedef int KeyType; //定义关键字类型为整数类型
typedef int InfoType;
typedef struct {
KeyType key; //关键字类型
InfoType info; //其他数据项类型
} RedType; //记录类型
typedef struct {
RedType r[MAX_SIZE+1]; //r[0]闲置或用作哨兵单元
int length; //顺序表长度
} SqList; //顺序表类型
void StraightInsertionSort1(SqList &L){
//对顺序表L做直接插入排序
for(int i=2; i<=L.length; ++i){
if(L.r[i].key < L.r[i-1].key){
L.r[0] = L.r[i];//复制为监视哨
int j;
for(j=i-1; L.r[0].key < L.r[j].key; --j){//此处重复比较了一次
L.r[j+1] = L.r[j];//记录后移
}
L.r[j+1] = L.r[0];//插入到正确位置
}
}
}
void StraightInsertionSort2(SqList &L){
//对顺序表L做直接插入排序
for(int i=2; i<=L.length; ++i){
if(L.r[i].key < L.r[i-1].key){
L.r[0] = L.r[i];//复制为监视哨
L.r[i] = L.r[i-1];
int j;
for(j=i-2; L.r[0].key < L.r[j].key; --j){
L.r[j+1] = L.r[j];//记录后移
}
L.r[j+1] = L.r[0];//插入到正确位置
}
}
}
1.2、排序的时间分析
实现排序的基本操作由两个:
1)“比较” 序列中两个关键字的大小;
2)“移动” 记录;
- 最好的情况(关键字在记录序列中顺序有序)
| “比较”的次数 | “移动”的次数 |
|---|---|
| ∑ i = 2 n 1 = n − 1 displaystylesum_{i=2}^{n} 1=n-1 i=2∑n1=n−1 | 0 |
- 最坏的情况(关键字在记录序列中逆序有序)
| “比较”的次数 | “移动”的次数 |
|---|---|
| ∑ i = 2 n i = ( n + 2 ) ( n − 1 ) 2 displaystylesum_{i=2}^{n} i=frac{(n+2)(n-1)}{2} i=2∑ni=2(n+2)(n−1) | ∑ i = 2 n ( i + 1 ) = ( n + 4 ) ( n − 1 ) 2 displaystylesum_{i=2}^{n} (i+1)=frac{(n+4)(n-1)}{2} i=2∑n(i+1)=2(n+4)(n−1) |
2、折半插入排序
2.1、思想与代码实现
在排序过程中,因为R[1 .. (i-1)]是一个按关键字有序的有序子序列,则可以利用折半查找实现 “在R[1 .. (i-1)]中查找R[i]的插入位置”,如此实现的插入排序为折半插入排序。
#define MAX_SIZE 20 //定义顺序表的最大长度
typedef int KeyType; //定义关键字类型为整数类型
typedef int InfoType;
typedef struct {
KeyType key; //关键字类型
InfoType info; //其他数据项类型
} RedType; //记录类型
typedef struct {
RedType R[MAX_SIZE+1]; //R[0]闲置或用作哨兵单元
int length; //顺序表长度
} SqList; //顺序表类型
//R[0]不存放数据元素
void BiInsertionSort(SqList &L){
for(int i=2; i<=L.length; ++i){
L.R[0] = L.R[i];//将L.R[i]暂存到L.R[0]
//在 L.R[1 .. i-1] 中折半查找插入位置;
int low=1, high=i-1;
while(low <= high){
int m = (low+high)/2; // 折半
if(L.R[0].key < L.R[m].key){
high = m - 1;//插入点在低半区
} else {
low = m + 1;//插入点在高半区
}//if
}//while
int j;
for(j=i-1; j>=high+1;--j){
L.R[j+1] = L.R[j];//记录后移
}//for
L.R[j+1] = L.R[0];//插入
}//for
}
2.2、排序的时间分析
待整理
3、表插入排序
为了减少在排序过程中进行的“移动”记录的操作,必须改变排序过程中采用的存储结构。利用静态链表进行排序,并在排序完成之后,一次性的调整各个记录相互之间的位置,即将每个记录都调整到他们所应该在的位置上。
3.1、思想与代码实现
使用静态链表完成表插入排序算法
void LInsertionSort(Elem SL[], int n){
//对记录序列SL[1..n]做表插入排序
SL[0].key = MAX_INT;
SL[0].next=1;
SL[1].next=0;
for(i=2; i<=n; ++i){
for(j=0,k=SL[0].next; SL[k].key<=SL[i].key;j=k,k=SL[k].next){
SL[j].next = i;
SL[i].next = k;
}//结点i 插入在 结点j 和 结点k 之间
}//for
}//LInsertionSort
// 如何在排序之后调整记录序列?
// 算法中使用了三个指针:
// p 指示第i个记录的当前位置;
// i 指示第i个记录应在的位置;
// q 指示第i+1个记录的当前位置;
void Arrange(Elem SL[], int n){
p = SL[0].next; //p指示第一个记录的当前位置
for(i=1; i<n; ++i){
while(p<i){
p = SL[p].next; //
}
q = SL[p].next; //q指示尚未调整的表尾
if(p != i){
SL[p] <-->SL[i]; //交换记录,使第i个记录到位
SL[i].next = p; //指向被移走的记录
}
p = q; //p指示尚未调整的表尾,为找第i+1个记录做准备
}//for
}//Arrange
3.2、排序的时间分析
待整理
4、希尔排序(缩小增量排序)
4.1、思想与代码实现
基本思想:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
//对顺序表L做一趟希尔插入排序。
//本算法是和一趟直接插入排序相比,做了如下修改:
//1、前后记录位置的增量是dk,而不是1;
//2、r[0]只是暂存单元,不是哨兵。当j<=0时,插入位置已找到。
void ShellInsert(SqList &L, int dk) {
for(int i=dk+1; i<=L.length; ++i) {
if(L.r[i].key < L.r[i-dk].key) {//需将 L.r[i] 插入有序增量子表
L.r[0] = L.r[i];//暂存在 L.r[0]
int j;
for(j=i-dk; j>0 && (L.r[0].key < L.r[j].key); j-=dk) {
L.r[j+dk] = L.r[j];//记录后移,查找插入位置
}
L.r[j+dk] = L.r[0];//插入
}
}
}
//按增量序列 dlta[0 .. t-1]对顺序表L做希尔排序
//SqList &L
//int dlta[] 增量序列
//int t 排序趟数
void ShellSort(SqList &L, int dlta[], int t) {
for(int k=0; k<t; ++t){
ShellInsert(L, dlta[k]);//一趟增量为dlta[k]的插入排序
}
}
4.2、排序的时间分析
待整理
后记
待整理
void ShellInsert(Elem R[], int dk){
for(int i=dk+1; i<=n; ++i){
if(R[i].key < R[i-dk].key){
R[0] = R[i];
int j;
for(j=i-dk; j>0 && (R[0].key < R[j].key); j-=dk){
R[j+dk] = R[j];
}
R[j+dk] = R[0];
}
}
}
void ShellSort(Elem R[], int dlta[], int t){
for(int k=0; k<t; ++t){
ShellInsert(R, dlta[k]);
}
}
——《数据结构图 (C语言版) 严蔚敏》 学习笔记
最后
以上就是机灵御姐最近收集整理的关于一、插入类排序1、直接插入排序2、折半插入排序3、表插入排序4、希尔排序(缩小增量排序)后记的全部内容,更多相关一、插入类排序1、直接插入排序2、折半插入排序3、表插入排序4、希尔排序(缩小增量排序)后记内容请搜索靠谱客的其他文章。








发表评论 取消回复