（数据结构）1.实现顺序查找的算法。 2.实现折半查找的算法。 3.实现二叉排序树的基本运算算法。

实验内容

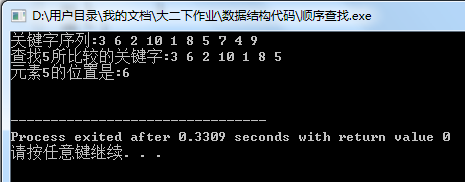
1、编写一个程序exp9-1.cpp，输出在顺序表（3,6,2,10,1,8,5,7,4,9）中采用顺序查找方法查找关键字5的过程。
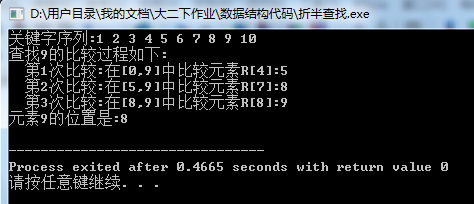
2、编写一个程序exp9-2.cpp，输出在顺序表（1,2,3,4,5,6,7,8,9,10）中采用折半查找方法查找关键字9的过程。
3、编写一个程序bst.cpp，包含二叉顺序树的创建、查找和删除算法，在此基础上编写exp9-4.cpp程序完成以下功能。
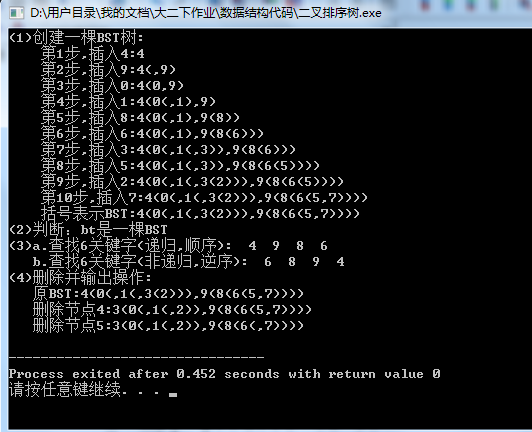
（1）由关键字序列（4,9,0,1,8,6,3,5,2,7）创建一棵二叉排bt并以括号表示法输出。
（2）判断bt是否为一棵二叉排序。
（3）采用递归和非递归两种方法查找关键字为6的结点，并输出其查找路径。
（4）分别删除bt中关键字为4和5的结点，并输出删除后的二叉排序。

代码实现

1、

#include <stdio.h>
#define MAXL 100     //定义表中最多记录个数
Typedef int KeyType;
typedef char InfoType[10];
typedef struct 
{ 
 		KeyType key;                  //KeyType为关键字的数据类型
   	 	InfoType data;                //其他数据
}NodeType;
typedef NodeType SeqList[MAXL];    //顺序表类型
int SeqSearch(SeqList R,int n,KeyType k) //顺序查找算法
{
    	int i=0;
    	while (i<n && R[i].key!=k) 
 		{
  			printf("%d ",R[i].key);
  			i++;     //从表头往后找
 		}
    	if (i>=n) 
  			return -1;
    	else 
 		{
  			printf("%d",R[i].key);
  			return i;
 		}
}
int main()
{
 		SeqList R;
 		int n=10,i;
 		KeyType k=5;
 		int a[]={3,6,2,10,1,8,5,7,4,9};
 		for (i=0;i<n;i++)    //建立顺序表
  			R[i].key=a[i];
 			printf("关键字序列:");
 		for (i=0;i<n;i++)
  			printf("%d ",R[i].key);
 		printf("n");
 		printf("查找%d所比较的关键字:",k);
 		if ((i=SeqSearch(R,n,k))!=-1)
  			printf("n元素%d的位置是:%dn",k,i);
 		else
  			printf("n元素%d不在表中n",k);
 		printf("n");
		return 0;
} 

结果截图：

2、

#include <stdio.h>
#define MAXL 100     //定义表中最多记录个数
typedef int KeyType;
typedef char InfoType[10];
typedef struct 
{ 
 	KeyType key;                 //KeyType为关键字的数据类型
    InfoType data;               //其他数据
}NodeType;
typedef NodeType SeqList[MAXL];    //顺序表类型
int BinSearch(SeqList R,int n,KeyType k) //二分查找算法
{
 	int low=0,high=n-1,mid,count=0;
 	while (low<=high) 
 	{ 
  		mid=(low+high)/2;
  		printf("  第%d次比较:在[%d,%d]中比较元素R[%d]:%dn",++count,low,high,mid,R[mid].key);
   		if (R[mid].key==k)    //查找成功返回
   			return mid;
  		if (R[mid].key>k)      //继续在R[low..mid-1]中查找
   			high=mid-1;
  		else
   			low=mid+1;        //继续在R[mid+1..high]中查找
 	}
 	return -1;
}

int main()
{
 	SeqList R;
 	KeyType k=9;
 	int a[]={1,2,3,4,5,6,7,8,9,10},i,n=10;
 	for (i=0;i<n;i++)    //建立顺序表
  		R[i].key=a[i];
 		printf("关键字序列:");
 	for (i=0;i<n;i++)
  		printf("%d ",R[i].key);
 		printf("n");
 		printf("查找%d的比较过程如下:n",k);
 	if ((i=BinSearch(R,n,k))!=-1)
  		printf("元素%d的位置是:%dn",k,i);
 	else
  		printf("元素%d不在表中n",k);
	return 0;
}

结果截图：

3、

#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
typedef int KeyType;     //定义关键字类型
typedef char InfoType;
typedef struct node                 //记录类型
{ 
 	KeyType key;                    //关键字项
    InfoType data;                 //其他数据域
    struct node *lchild,*rchild;  //左右孩子指针
}BSTNode;
int path[MaxSize];      //全局变量,用于存放路径
void DispBST(BSTNode *b);    //函数说明
int InsertBST(BSTNode *&p,KeyType k) //在以*p为根节点的BST中插入一个关键字为k的节点
{
    if (p==NULL)      //原树为空, 新插入的记录为根节点
 	{
  		p=(BSTNode *)malloc(sizeof(BSTNode));
  		p->key=k;p->lchild=p->rchild=NULL;
  		return 1;
 	}
 	else if (k==p->key) 
  		return 0;
 	else if (k<p->key) 
  		return InsertBST(p->lchild,k); //插入到*p的左子树中
 	else  
  		return InsertBST(p->rchild,k);  //插入到*p的右子树中
}
BSTNode *CreatBST(KeyType A[],int n)    
//由数组A中的关键字建立一棵二叉排序树
{
   	BSTNode *bt=NULL;            //初始时bt为空树
    int i=0;
    while (i<n) 
    { 
  		if (InsertBST(bt,A[i])==1)  //将A[i]插入二叉排序树T中
  		{
   			printf("    第%d步,插入%d:",i+1,A[i]);
   			DispBST(bt);printf("n");
   			i++;
  		}
  	} 
    return bt;                  //返回建立的二叉排序树的根指针
}
void Delete1(BSTNode *p,BSTNode *&r)
//当被删*p节点有左右子树时的删除过程
{
 	BSTNode *q;
 	if (r->rchild!=NULL)
  		Delete1(p,r->rchild); //递归找最右下节点
 	else      //找到了最右下节点*r
 	{
  		p->key=r->key;   //将*r的关键字值赋给*p
  		q=r;     
  		r=r->lchild;   //将*r的双亲节点的右孩子节点改为*r的左孩子节点
  		free(q);    //释放原*r的空间
 	}
}
void Delete(BSTNode *&p)
//从二叉排序树中删除*p节点
{
 	BSTNode *q;
 	if (p->rchild==NULL)  //*p节点没有右子树的情况
 	{
  		q=p;p=p->lchild;free(q);
 	}
 	else if (p->lchild==NULL) //*p节点没有左子树的情况
 	{
  		q=p;p=p->rchild;free(q);
 	}
 	else 
	 	Delete1(p,p->lchild); //*p节点既有左子树又有右子树的情况
}
int DeleteBST(BSTNode *&bt,KeyType k) 
//在bt中删除关键字为k的节点
{
 	if (bt==NULL) return 0;  //空树删除失败
 	else 
 	{
  		if (k<bt->key) 
   			return DeleteBST(bt->lchild,k);  //递归在左子树中删除关键字为k的节点
  		else if (k>bt->key) 
   			return DeleteBST(bt->rchild,k);  //递归在右子树中删除关键字为k的节点
  		else         //k=bt->key的情况
  		{
   			Delete(bt);  //调用Delete(bt)函数删除*bt节点
   			return 1;
  		}
 	}
}
void SearchBST1(BSTNode *bt,KeyType k,KeyType path[],int i) 
//以非递归方式输出从根节点到查找到的节点的路径
{ 
 	int j;
 	if (bt==NULL)
  		return;
 	else if (k==bt->key) //找到了节点
 	{
  		path[i+1]=bt->key; //输出其路径
  		for (j=0;j<=i+1;j++)
   		printf("%3d",path[j]);
  		printf("n");
 	}
 	else
 	{
  		path[i+1]=bt->key;
  		if (k<bt->key)
   			SearchBST1(bt->lchild,k,path,i+1);  //在左子树中递归查找
  		else
   			SearchBST1(bt->rchild,k,path,i+1);  //在右子树中递归查找
 	}
}
int SearchBST2(BSTNode *bt,KeyType k) 
//以递归方式输出从根节点到查找到的节点的路径
{ 
 	if (bt==NULL)
  		return 0;
 	else if (k==bt->key)
 	{
  		printf("%3d",bt->key);
  		return 1;
 	}
 	else if (k<bt->key)
  		SearchBST2(bt->lchild,k);  //在左子树中递归查找
 	else
  		SearchBST2(bt->rchild,k);  //在右子树中递归查找
 		printf("%3d",bt->key);
}

void DispBST(BSTNode *bt) 
//以括号表示法输出二叉排序树bt
{
 	if (bt!=NULL)
 	{
  		printf("%d",bt->key);
  		if (bt->lchild!=NULL || bt->rchild!=NULL)
  		{
   			printf("(");
   			DispBST(bt->lchild);
   			if (bt->rchild!=NULL) 
	   			printf(",");
   				DispBST(bt->rchild);
   				printf(")");
  		}
 	}
}
KeyType predt=-32767; //predt为全局变量,保存当前节点中序前趋的值,初值为-∞
int JudgeBST(BSTNode *bt) //判断bt是否为BST
{
 	int b1,b2;
 	if (bt==NULL)
  		return 1;
 	else 
 	{
  		b1=JudgeBST(bt->lchild);
  		if (b1==0 || predt>=bt->key)
   			return 0;
  			predt=bt->key;
  			b2=JudgeBST(bt->rchild);
  			return b2;
 	}
}
int main()
{
 	BSTNode *bt;
 	KeyType k=6;
 	int a[]={4,9,0,1,8,6,3,5,2,7},n=10;
 	printf("(1)创建一棵BST树:");
 	printf("n");
 	bt=CreatBST(a,n);
 	printf("    括号表示BST:");DispBST(bt);printf("n");
 	printf("(2)判断：bt%sn",(JudgeBST(bt)?"是一棵BST":"不是一棵BST"));
 	printf("(3)a.查找%d关键字(递归,顺序):",k);SearchBST1(bt,k,path,-1);
	printf("   b.查找%d关键字(非递归,逆序):",k);SearchBST2(bt,k);
 	printf("n(4)删除并输出操作:n");
 	printf("   原BST:");DispBST(bt);printf("n");
 	printf("   删除节点4:");
 	DeleteBST(bt,4);
 	DispBST(bt);printf("n");
 	printf("   删除节点5:");
 	DeleteBST(bt,5);
 	DispBST(bt);
 	printf("n");
 	return 0; 
}

结果截图：

最后

以上就是优雅冰淇淋为你收集整理的（数据结构）1.实现顺序查找的算法。 2.实现折半查找的算法。 3.实现二叉排序树的基本运算算法。的全部内容，希望文章能够帮你解决（数据结构）1.实现顺序查找的算法。 2.实现折半查找的算法。 3.实现二叉排序树的基本运算算法。所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。