快速排序原理及实现

59 阅读 0 评论 39 点赞

我是靠谱客的博主机灵高跟鞋，最近开发中收集的这篇文章主要介绍快速排序原理及实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

转自博客：http://blog.csdn.net/morewindows/article/details/6684558
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高，因此经常被采用，再加上快速排序思想—-分治法也确实实用，因此很多软件公司的笔试面试，包括像腾讯，微软等知名IT公司都喜欢考这个，还有大大小的程序方面的考试如软考，考研中也常常出现快速排序的身影。

该方法的基本思想是：

1．先从数列中取出一个数作为基准数。
2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
3．再对左右区间重复第二步，直到各区间只有一个数。

虽然快速排序称为分治法，但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明：挖坑填数+分治法：
先来看实例吧，定义下面再给出（最好能用自己的话来总结定义，这样对实现代码会有帮助）。

首先以一个数组作为示例，取区间第一个数为基准数。
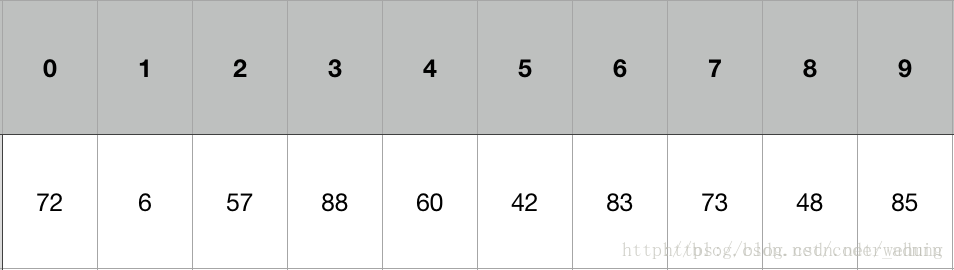
这里写图片描述

1 初始值：i = 0;  j = 9;  X = a[i] = 72

由于已经将a[0]中的数保存到X中，可以理解成在数组a[0]上挖了个坑，可以将其它数据填充到这来。

从j开始向前找一个比X小或等于X的数。当j=8，符合条件，将a[8]挖出再填到上一个坑a[0]中。a[0]=a[8]; i++; 这样一个坑a[0]就被搞定了，但又形成了一个新坑a[8]，这怎么办了？简单，再找数字来填a[8]这个坑。这次从i开始向后找一个大于X的数，当i=3，符合条件，将a[3]挖出再填到上一个坑中a[8]=a[3]; j–;

数组变化结果：
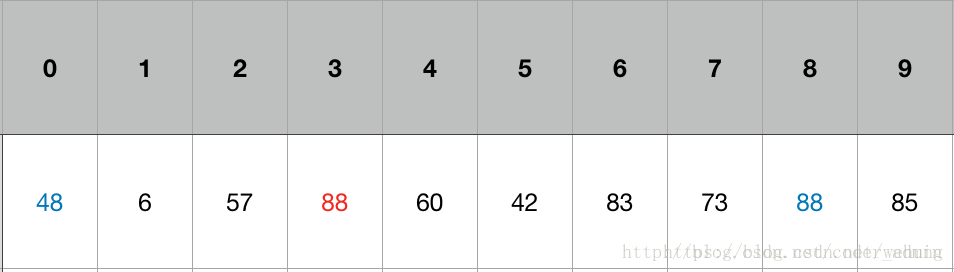
这里写图片描述

i = 3;  j = 7;  X=72

再重复上面的步骤，先从后向前找，再从前向后找。
从j开始向前找，当j=5，符合条件，将a[5]挖出填到上一个坑中，a[3] = a[5]; i++;
从i开始向后找，当i=5时，由于i==j退出。
此时，i = j = 5，而a[5]刚好又是上次挖的坑，因此将X填入a[5]。

数组再次变化：
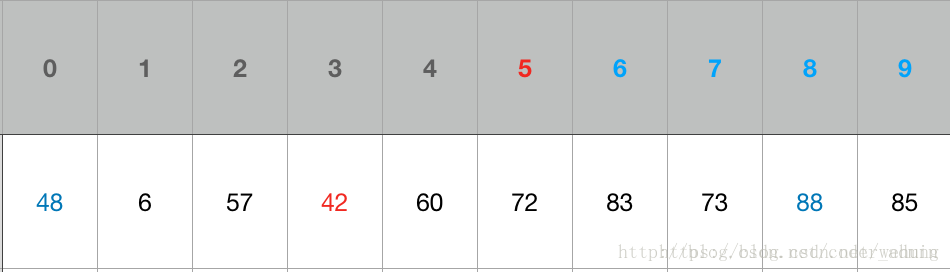
这里写图片描述
可以看出a[5]前面的数字都小于它，a[5]后面的数字都大于它。因此再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。

对挖坑填数进行总结

1．i =L; j = R; 将基准数挖出形成第一个坑a[i]。

2．j–由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。

3．i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。

4．再重复执行2，3二步，直到i==j，将基准数填入a[i]中。

照着这个总结很容易实现挖坑填数的代码：

//返回调整后基准数的位置
int AdjustArray(int s[], int l, int r) {
    int i = l, j = r;
    int x = s[l]; //s[l]即s[i]就是第一个坑
    while (i < j){
        // 从右向左找小于x的数来填s[i]
        while(i < j && s[j] >= x) 
            j--;  
        if(i < j) {
            //将s[j]填到s[i]中，s[j]就形成了一个新的坑
            s[i] = s[j]; 
            i++;
        }

        // 从左向右找大于或等于x的数来填s[j]
        while(i < j && s[i] < x)
            i++;  
        if(i < j) {
            //将s[i]填到s[j]中，s[i]就形成了一个新的坑
            s[j] = s[i]; 
            j--;
        }
    }
    //退出时，i等于j。将x填到这个坑中。
    s[i] = x;
    return i;
}

再写分治法的代码

void quick_sort1(int s[], int l, int r){
    if (l < r){
        int i = AdjustArray(s, l, r);//先成挖坑填数法调整s[]
        quick_sort1(s, l, i - 1); // 递归调用 
        quick_sort1(s, i + 1, r);
    }
}

这样的代码显然不够简洁，对其组合整理下：

//快速排序
void quick_sort(int s[], int l, int r){
    if (l < r){
        //Swap(s[l], s[(l + r) / 2]); 
        //将中间的这个数和第一个数交换 参见注1
        int i = l, j = r, x = s[l];
        while (i < j){
            // 从右向左找第一个小于x的数
            while(i < j && s[j] >= x) {
                j--;  
            }
            if(i < j) {
                s[i++] = s[j];
            }
            // 从左向右找第一个大于等于x的数
            while(i < j && s[i] < x){
                i++;  
            }
            if(i < j) {
                s[j--] = s[i];
            }   
        }
        s[i] = x;
        quick_sort(s, l, i - 1); // 递归调用 
        quick_sort(s, i + 1, r);
    }
}

快速排序还有很多改进版本，如随机选择基准数，区间内数据较少时直接用另的方法排序以减小递归深度。有兴趣的筒子可以再深入的研究下。

注1，有的书上是以中间的数作为基准数的，要实现这个方便非常方便，直接将中间的数和第一个数进行交换就可以了
python程序：来自数据结构（python语言描述）

def quick_sort(lists):
    quick_rec(lists, 0, len(lists)-1)
    return lists


def quick_rec(lists, l, r):
    if l >= r:
        return
    i = l
    j = r
    pivot = lists[i]
    while i < j:
        while i <j and lists[j] > pivot: # 用j向左扫描小于pivot的值
            j -= 1
            if i < j:
                lists[i] = lists[j]
        while i < j and lists[i] < pivot:# 用i向右扫描大于pivott的值
            i += 1
            if i < j:
                lists[j] = lists[i]
        lists[i] = pivot
        quick_rec(lists, l, i-1)
        quick_rec(lists, i+1, r)


print(quick_sort([5, 1, 4, 2, 9]))