1.线性表

0.1定义链表结构体

struct LinkList{
  int data;
  LinkList *next;
};

1.1.1逆转顺序表所有元素

第一个元素和第n个元素对调

void Reserve(int A[],int N){
  int i,t;
  for (i=0;i<2/n;i++){
    t=A[i];
    A[i]=A[n];
    A[n]=t;
  }
}
  

1.1.2删除线性链表中数据域为item的所有节点

从第二个节点开始，从前往后判断，满足条件则删去，最后再判断第一个节点是否满足条件，满足则删去

void PurgetItem(LinkList &List)
{
  LinkList p,q=list;
  p=List->next;
  while(p!=NULL)
  {
   if(p->data==item)
   {
     q->next=p->next;
     free(p);
   }
    else
   {
     q=p;
     p=p->next;
   }
  }
  if(List->data==item)
  {
    q=list;
    list=list->next;
    free(q);
  }
}

1.1.3逆转线性链表

void Reserve(LinkList &list)
{
  LinkList p,q,r;
  p=list;
  q=null;
  if(p!=NULL)
  {
    r=q;
    q=p;
    p=p->next;
    q->next=r;
  }
  list=q;
  
}

1.1.4复制链表

LinkList copy(LinkList lista)
{
  LinkList listb;
  if(lista==NULL)
    return NULL;
  else
  {
    listb=(ListList)malloc(sizeof(LNode));//分配空间
    listb->data=lista->data;
    listb->next=copy(list->next);
    return listb;
  }
  
}

1.1.5将两个有序排列的非空并成一个按值有序的线性链表

LinkList mergeList(LinkList lista,Link listb)
{
  LinkList listc;
  LinkList p=lista,q=listb,r;
  //listc指向两个链表中所指结点较小的那一个
  //初始化操作
  if(lista->data<listb->data)
  {
    listc=lista;
    r=lista;
    p=lista->next;
  }else
  {
    listc=listb;
    r=listb;
    q=q->next;
  }
  
 //正式开始对比
  while(p!=NULL&&q!=NULL)
  {
    if(p->data<q->data)
    {
      r->next=p;
      r=p;
      p=p->next;
    }else
    {
      r->next=q;
      r=q;
      q=q->next;
    }
    r-next=(p!=NULL)?p:q;
    return listc;
  }
}

1.1.5.2合并有序链表 递归

void mergeList(LinkList lista,LinkList listb;LinkList listc)
{
  if(lista=NULL)
    return listb;
  else(listb=NULL)
    return lista;
  while(lista&&listb)
  {
    if(lista->data<listb->data)
    {
      L=lista;
      L->next=merge(lista->next,listb,L);
    }
    else
    {
      L=listb;
      L->next=merge(lista,listb->next,L);
    }
    return L;
  }
  
}

2.栈和队列

2.1栈

0.定义栈的结构体（链表）

typedef struct Node{
    char s;
    struct Node* next;
}node,*pnode;

typedef struct Stack{
    pnode ptop;
    pnode pbase;//定义栈顶和栈底指针（数组下标）
}stack,*pstack;

2.1.1括号匹配

bool brackCheck(char [str],int length)
{
  Stack S;
  InitStack(S);//初始化一个栈
  for(int i=0;i<length;i++)
  {
    if(str[i]=='('||str[i]=='['||str[i]=='{')
    {
 			Push(S,str[]);//扫描到左括号，入栈      
    }else
    {
      char topElem;
      Pop(S,topElem);//出栈操作
    	if(str[i]==')'&&topElem!='(')
        return false;
      if(str[i]==']' && topElem!='[')
            return false;
      if(str[i]=='}' && topElem!='{')
            return false;
       if(StackEmpty(S))
        return false;
    }
    
  }
}

2.1.2进制转换

void Conversion(){//十进制转16进制
  Stack S;
  InitStack (S);
  cin>>N;//输入一个正整数
  while(N!=0){
    Push(S,N%16);//让
      N=N/16;
  }
  while(IsEmpty(s)!=NULL){
    pop(kS,e);
    cout<<e;
  }
  
}

2.1.3表达式求值

中缀表达式转后缀表达式

void tranform (char suffix[],char exp[])
{
  InitStack(S);
  Push(s,'#');
  p=exp;
  ch=*p;
  while(!StackEmpty(S)
        {
   if(!IN(ch,op))//判断ch是不是操作符，IN函数比较ch是否是op(操作符)
     Pass(suffix,ch);//如果不是操作符，则直接发给后缀式
    else
    {
      switch(ch)
      {
					case'(':Push(S,ch); //左括号的进栈优先级最大直接进栈（比任何栈内的运算符出栈优先级都大
          break;
          case')':{ //右括号的的出栈优先级最大直接出栈（比任何栈外的运算符进栈优先级都大
            Pop(S,c);
            while(c!='('){//出栈的不为'（'时加入后缀表达式
                        Pass(suffix,c);//发送给后缀表达式
                        Pop(S,c);
                        }
       }
          break;
        default:{ //其他情况，则根据入栈的运算符优先级（与栈顶元素的出栈优先级比较）决定此运算符直接加入后缀表达式还入栈
                    //如果ch的入栈优先级大于站内元素的出栈优先级，则进栈，ComparePr()函数是判断入栈优先级大于站内元素的出栈优先级，是返回1，否返回false
              op1 = Gettop(S,c);//op1为栈顶元素
                    if(ComparePr(ch,op1)==1)
                    {
                        Push(S,ch);
                    }
                    else if(ch!='#')
                        Push(S,ch);                        
                    else
                        Pass(suffix,c);
                }
                break;
                    }
                }
        if(ch!='#')
        {
            p++;
            ch=*p;
         }
          
      }
    }
  }
}

2.1.4在循环队列中插入一个元素

bool EnQueue(SqQueue &Q,ElemType e)
{
		if((Q.rear+1)%MS==Q.front)//判断循环队列是否满
        return false;
    Q.data[Q.rear] = e;//留一个不用
    Q.rear =(Q.rear+1)%MS;
    return true;
}

2.2队列

2.2.1拓扑排序

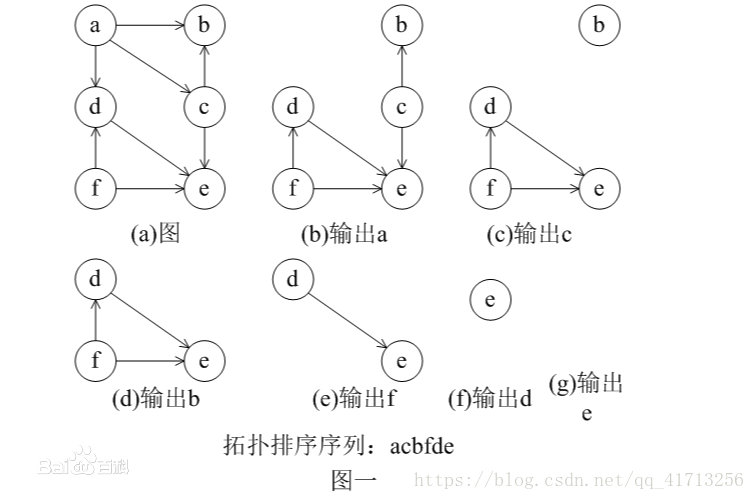
//b[]为每个点的入度
for(i=1;i<=n;i++){
   for(j=1;j<=n;j++){
      if(b[j]==0){   //找到一个入度为0的点
        ans=j;
        vis[cnt++]=j;
        b[j]--;
        break;
       }
    }
    for(j=1;j<=n;j++)
        if(a[ans][j]) b[j]--; //与入度为0的点相连的点的入度减一
}
    printf("%d",vis[0]);
    for(i=1;i<cnt;i++) printf(" %d",vis[i]);
    printf("n");

3.树

0.二叉树的链式存储结构

typedef struct Btree{
  Elemtype data;//数据域
  struct Btree *child,*rchild;//左右指针
}*Btree;

0.0建立二叉树

（从键盘输入，先序遍历递归算法）

Btree CreateBT()
{
  char ch;
  BTree T;
  scanf("%c",&ch);
  if(ch=='-')
    return NULL;//以-作为空结点
  else{
    T(BTree)malloc(sizeof(BTNode));//创立节点
    T->data=ch;
    T->lchild=CreateBT();
    T->rchild=CreateBT();
  }
  return T;
}

3.1.1二叉树的先序遍历（递归

void PreOrder(Btree T)
{
  if(T)
  {
    visit(T);
    PreVisit(T->*lchild);
    PreVisit(T->*rchild);
  }
}

3.1.2二叉树的中序遍历（递归

void PreOrder(Btree T)
{
  if(T)
  {
    PreVisit(T->*lchild);
    visit(T);
    PreVisit(T->*rchild);
  }
}

3.1.3二叉树的后序遍历（递归

void PreOrder(Btree T)
{
  if(T)
  {
    PreVisit(T->*lchild);
    PreVisit(T->*rchild);
    visit(T);
  }
}

3.1.4 递归应用：求根节点的WPL

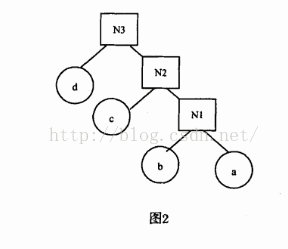
WPL=各叶子结点的带权路径之和

//先序遍历
int WPL(Btree root){
return wpl_PreOrder(root,0);
}
//WPL=∑（叶节点的权值）*（叶节点的深度）
int wpl-PreOrder(Btree root,int deep){
   int wpl=0;
  if(root->lchild==NULL&&root->rchild==NULL)
  {
    wpl+=deep*root->weight;
  }
  if(root->lchild!=NULL)
  {
    wpl_PreOrder(root->lchild,deep+1);
  }
  if(root->rchild!=NULL)
  {
    wpl_PreOrder(root->rchild,deep+1);
  }
  return wpl;
}
//层序遍历
int wpl_LevelOrder(BTree root){
    LinkQueue Q;//定义队列
    InitQueue(Q);
    TreeNode * lastNode  = root;
    TreeNode * newlastNode = NULL; //用来记录下一层最后一个结点
    TreeNode *t;//接受出栈的元素
    int wpl = 0,deep=0;
    while(!IsEmpty(Q)){
        DeQuenue(S,t);//从队头出队
        if(t->lchild==NULL&&t->rchild==NULL)
            wpl +=deep*t->weight;
        if(t->lchild !=NULL){
            EnQuenue(S,t->lchild);
            newlastNode = t->lchild;
        }
        if(t->rchild != NULL){
            EnQuenue(S,t->rchild);
            newlastNode = t->rchild;
        }
        if(t->rchild == lastNode){
            lastNode = newlastNode;
            deep++;
        }
    }
    return wpl;
}

3.1.5求二叉树深度

int Depth(Btree T)
{
  int ldepth,rdepth;
  if(T==NULL)
    return 0;
 else{
   ldepth=Depth(T->lchild);
   rdepth=Depth(T->rchild);
 }
}

4.图

4.0图的存储。

4.1图的遍历

4.1.1广度优先遍历

类似二叉树的层次遍历

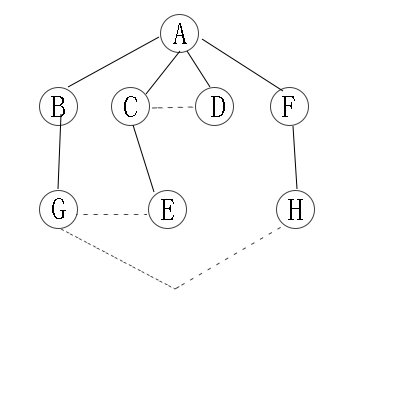
因此访问顺序是：A -> B -> C -> D -> F -> G -> E -> H

bool visited[MAX_VERTEX_MAX];
void BFSTraverse(Graph G){
	for(i=0;i<G.vexnum;++i)
        visited[i]=false;
    InitQueue(Q);
    for(i=0;i<G.vexnum;++i){
        if(!visited[i])
            BFS(G,i);
    }
}
void BFS(Graph G,int v){
    visit(v);
    visited[v]=true;
    Enqueue(Q,v);
    while(!isEmpty(Q)){
        Dequeue(Q,v);        for(w=FirstNeighbour(G,v);w>=0;w=NextNeighbour(G,v,w))
            if(!visited[w]){
                visit(w);
                visited[w]=true;
                Enqueue(Q,w);
            }
    }
}

4.1.2深度优先遍历(Depth First Search)

类似图的先序遍历

深度优先遍历的主要思想是：

1、首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点；2、当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直至所有的顶点都被访问过。

//递归
void DFS(A,n.v){
    visit(v);
    visited[v]=1;
    for(int j=1;j<=n;j++){
        if(A[v][j]==1 &&visited[j] == 0){
            DFS(A,n,j);
        }
    }
}

应用：逆拓扑排序
//一般情况
bool visited[MAX_VERTEX_NUM];
void DFSTraverse(Graph G){
    for(v=0;v<G.vexnum;++v)
        visit[v]=false;
    for(v=0;v<G.vexnum;++v){
        if(!visited[v])
            DFS(G,v);
    }
}
void DFS(Graph G,int v){
    visit(v);
    visited[v]=true;    
    for(w=FirstNeighour(G,v);w>=0;w=NextNeighour(G,v,w))
        if(!visited[w]){
            DFS(G,w);
        }
}

最后

以上就是冷酷马里奥为你收集整理的数据结构常见算法总结1.线性表2.栈和队列3.树4.图的全部内容，希望文章能够帮你解决数据结构常见算法总结1.线性表2.栈和队列3.树4.图所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。