文章目录
- 简介
- 选择排序
- 思路和图示
- 算法度量
- 代码
- 插入排序
- 思路和图示
- 代码
- 和冒泡算法的比较
- 三种算法异同的助记图
简介
教科书和很多网上文章对选择和插入算法介绍都大同小异, 他们的概念看起来很相似, 很让人迷糊. 这篇博客好好总结他们的异同点, 彻底征服他们.
选择排序
思路和图示
假设进行从小到大的排序, 文字步骤描述如下:
- 新增一个数列来装数据.
- 每一次循环从原始数列找出一个最小值, 放到新数列.
- 重复第2步. 这样原始数列会越来越小, 直到处理完毕.
- 返回新的数列, 将原始数列的内存释放.
图示如下:
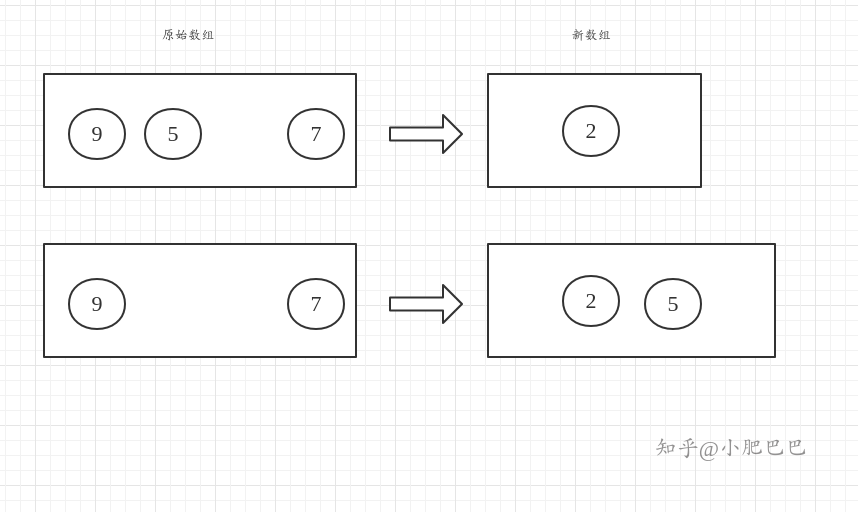
这样一看思路清晰多了.
然后你再次思考会发现: 其实没有必要增加一个新数列, 原始数列和"新数列"的长度是一样的, 而且每次处理都不会涉及已处理过的数据, 所以你可以在原有数列就进行处理, 因此这个图又可以优化成这样:
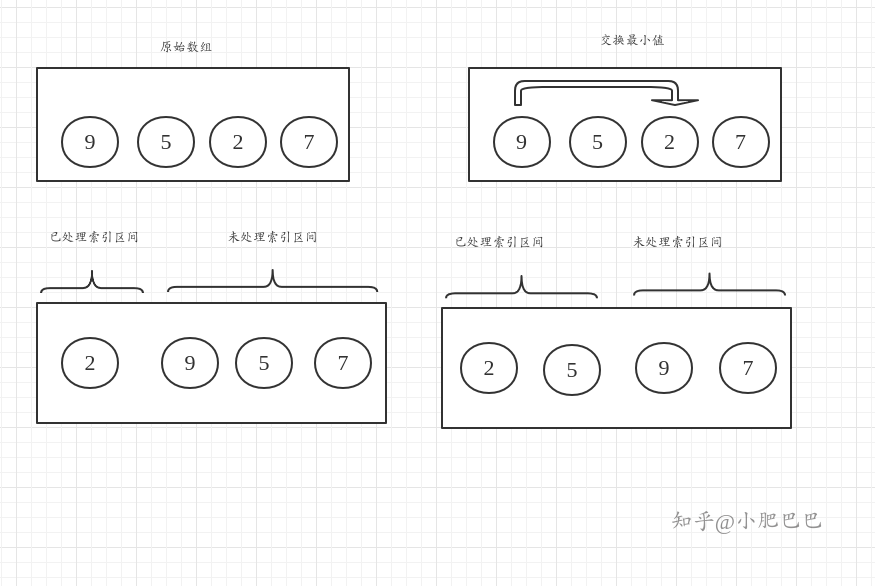
这时候算法的步骤可以进一步描述如下:
- 将原始数列考虑成已处理索引区间和未处理索引区间两部分.
- 每次循环从未处理索引区间取出一个最小值, 放入到已处理索引区间的末端. (由于是在同一个数列进行操作, 其实就是交换值)
- 重复第二步, 直到处理完所有的未处理索引.
这就是多数教科书的算法描述了, 其实既包含了算法的思想, 也包含了后来恍然大悟的优化思维. 如果不优化直接用两个数列处理, 程序就会非常简单和形象, 但是增加内存消耗.
算法度量
如果数列长度是n, 那么未处理索引区间一开始是n, 后来是n + 1 , 步骤如下:
i = 0 : 需要遍历 n 个数值
i = 1 : 需要遍历 n - 1 个数值
i = 2 : 需要遍历 n - 2 个数值
…
因此总时间(操作数) 是 n + (n - 1) + (n - 2) + … + 0 = ( 1 + n ) * n / 2
即O(n2)
代码
为了让概念更清晰, 我将辅助函数剔除, 核心主程序在这:
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21def selection_sort(data_list, sort='asc'): # sort 是 asc (从小到大) 或者 desc (从大到小) size = len(data_list) for i in range(0, size): if sort == 'asc': # 如果是升值排序, 查找最小值的index index = find_min(data_list, i, size) else: # 查找最大值的index index = find_max(data_list, i, size) if index == i: # 自己不需要和自己交换 continue exchange_value(data_list, i, index)
简单吧? 可以说选择排序是最直观的算法.
完整的程序如下:
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84#! /usr/bin/python # -*- coding: UTF-8 -*- """ 作者: 小肥巴巴 简书: https://www.jianshu.com/u/db796a501972 邮箱: imyunshi@163.com github: https://github.com/xiaofeipapa/algo_example 您可以任意转载, 恳请保留我作为原作者, 谢谢. """ def exchange_value(data_list, index, other_index): temp = data_list[index] data_list[index] = data_list[other_index] data_list[other_index] = temp def find_min(data_list, j, size): min_value = data_list[j] min_index = j for x in range(j + 1, size): if min_value > data_list[x]: min_value = data_list[x] min_index = x return min_index def find_max(data_list, j, size): max_value = data_list[j] max_index = j for x in range(j + 1, size): if max_value < data_list[x]: max_value = data_list[x] max_index = x return max_index def selection_sort(data_list, sort='asc'): # sort 是 asc (从小到大) 或者 desc (从大到小) size = len(data_list) for i in range(0, size): if sort == 'asc': # 如果是升值排序, 查找最小值的index index = find_min(data_list, i, size) else: # 查找最大值的index index = find_max(data_list, i, size) if index == i: # 自己不需要和自己交换 continue exchange_value(data_list, i, index) def test_it(): data_list = [5, 4, 10, 2, 7] selection_sort(data_list) print('==== 排序后: ', data_list) data_list = [5, 4, 10, 2, 7] selection_sort(data_list, 'desc') print('==== 排序后: ', data_list) if __name__ == '__main__': test_it()
插入排序
思路和图示
插入排序和选择排序其实都有"插入"的行为(在原始数列是交换值的操作), 那么有什么区别呢? 先来看看插入排序的概念:
- 将原始队列视为未处理索引区间和已处理索引区间( 第一步想法和选择排序是一样的) .
- 每一次循环取一个值, 插入到已处理索引区间. (和选择排序不同)
- 由于无法确定插入的具体位置, 所以和已处理索引区间的各个值比较, 找到合适的插入位置.
- 重复2-3步.
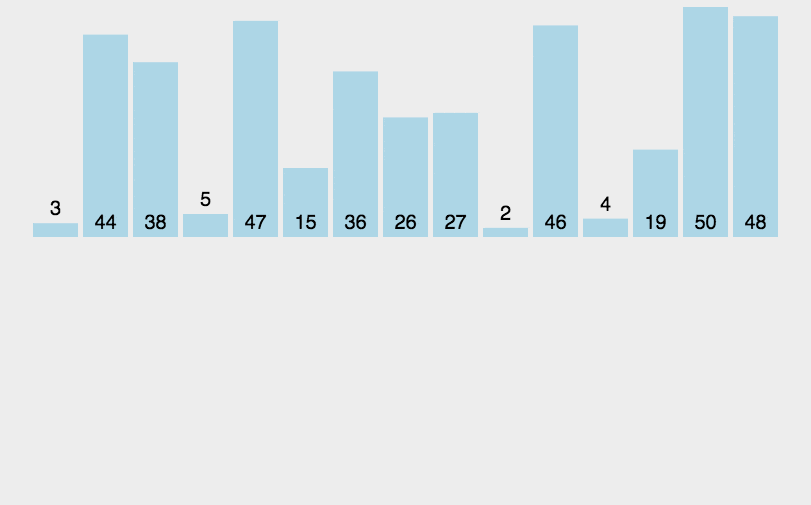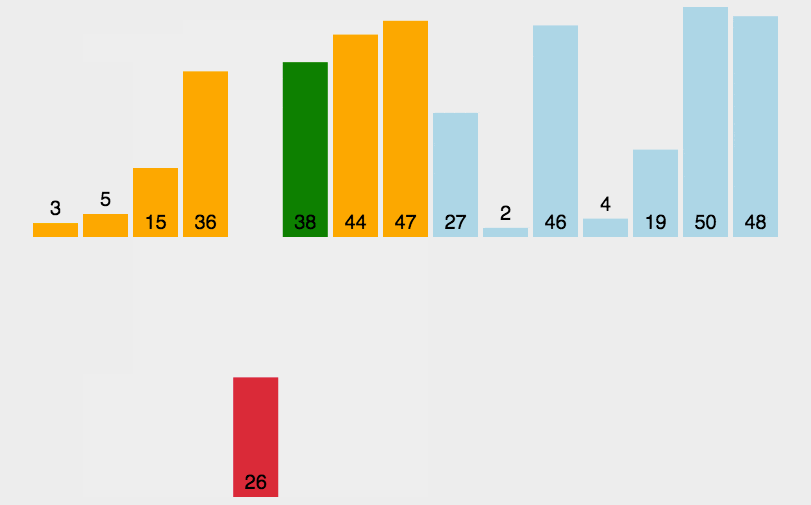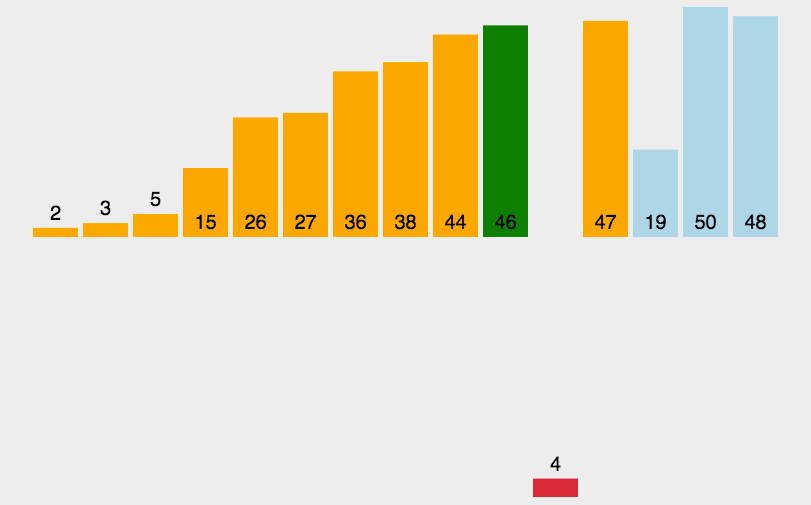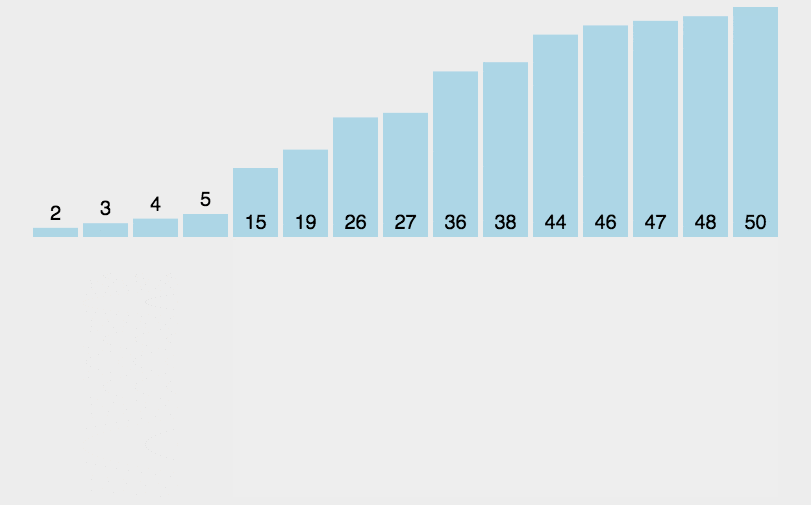
用之前的图示法, 画图如下:
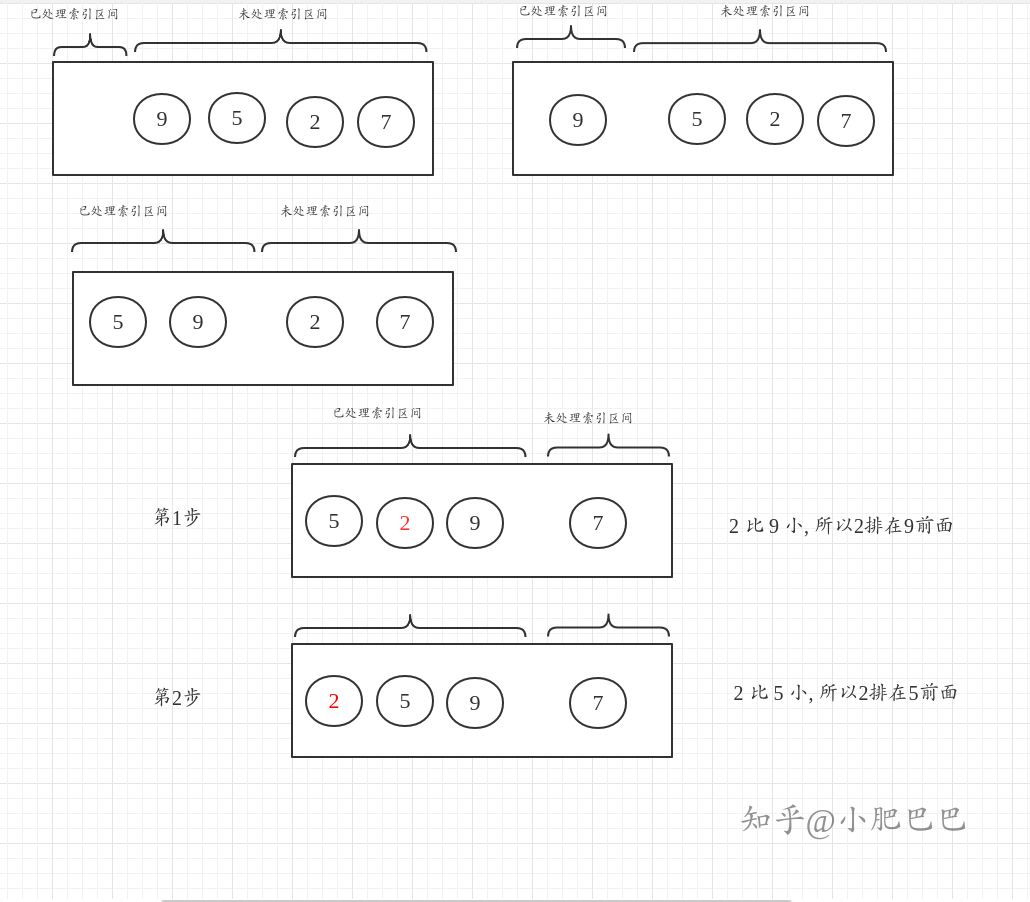
用来对比选择排序, 两者的区别就很明显了:
- 两种算法都有"选择", “插入” 的过程
- 选择算法的侧重点在"选择", 在选择的过程就找出了最值, 所以插入处理简单.
- 插入算法的侧重点在"插入", 选择的过程只是按顺序取数, 在插入的时候需要确定最值位置.
在网上找到一个不错的动图: https://www.runoob.com/w3cnote/insertion-sort.html
代码
算法的代码如下:
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24def insertion_sort(data_list, sort='asc'): # sort 是 asc (从小到大) 或者 desc (从大到小) size = len(data_list) # 索引为0的元素不必移动, 所以从1开始 for i in range(1, size): j = i # 子区间的操作 while j >= 1: # 如果是升值排序 if sort == 'asc' and data_list[j] < data_list[j-1]: exchange_value(data_list, j, j-1) # 如果是降序 if sort == 'desc' and data_list[j] > data_list[j - 1]: exchange_value(data_list, j, j - 1) j -= 1
完整的程序如下:
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61#! /usr/bin/python # -*- coding: UTF-8 -*- """ 作者: 小肥巴巴 简书: https://www.jianshu.com/u/db796a501972 邮箱: imyunshi@163.com github: https://github.com/xiaofeipapa/algo_example 您可以任意转载, 恳请保留我作为原作者, 谢谢. """ def exchange_value(data_list, index, other_index): temp = data_list[index] data_list[index] = data_list[other_index] data_list[other_index] = temp def insertion_sort(data_list, sort='asc'): # sort 是 asc (从小到大) 或者 desc (从大到小) size = len(data_list) # 索引为0的元素不必移动, 所以从1开始 for i in range(1, size): j = i # 子区间的操作 while j >= 1: # 如果是升值排序 if sort == 'asc' and data_list[j] < data_list[j-1]: exchange_value(data_list, j, j-1) # 如果是降序 if sort == 'desc' and data_list[j] > data_list[j - 1]: exchange_value(data_list, j, j - 1) j -= 1 def test_it(): data_list = [5, 4, 10, 2, 7] insertion_sort(data_list) print('==== 排序后: ', data_list) data_list = [5, 4, 10, 2, 7] insertion_sort(data_list, 'desc') print('==== 排序后: ', data_list) if __name__ == '__main__': test_it()
和冒泡算法的比较
插入算法和冒泡算法在核心代码上很像, 比较如下:
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37# ====== 插入算法 for i in range(1, size): j = i # 子区间的操作 while j >= 1: # 如果是升值排序 if sort == 'asc' and data_list[j] < data_list[j-1]: exchange_value(data_list, j, j-1) # 如果是降序 if sort == 'desc' and data_list[j] > data_list[j - 1]: exchange_value(data_list, j, j - 1) j -= 1 # ===== 冒泡算法 for i in range(0, size): for j in range(0, size): # 已经是最后一位 if j == size - 1: break # 如果是升值排序 if sort == 'asc' and data_list[j] > data_list[j+1]: exchange_value(data_list, j, j+1) # 如果是降序 if sort == 'desc' and data_list[j] < data_list[j+1]: exchange_value(data_list, j, j+1)
两者的区别要画图或者看动态图才能感受出来, 文字描述是:
- 两者都有一个循环需要比较相邻的数(称为比较循环吧)
- 冒泡算法的循环过程是从左向右操作 (>) , 而插入算法的循环过程是从右向左. ( <)
- 在冒泡算法的比较循环中, 每一个数只会移动一次. 而插入算法的数可能移动多次.
三种算法异同的助记图
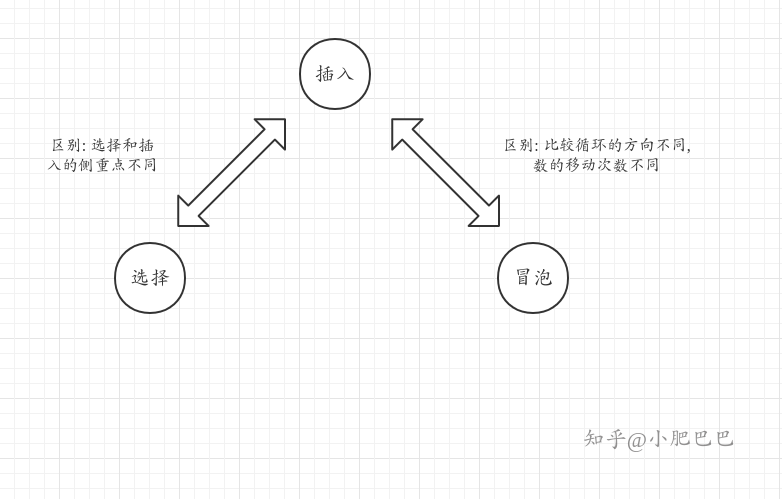
收工!
最后
以上就是活泼猫咪最近收集整理的关于选择和插入排序简介选择排序插入排序三种算法异同的助记图的全部内容，更多相关选择和插入排序简介选择排序插入排序三种算法异同内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复