排序算法
本篇博客仅给出
6
6
6 种基础排序算法的原理、时间复杂度分析和代码实现(
C
C
C++,
P
y
t
h
o
n
Python
Python 和
J
a
v
a
Java
Java),其他更高级的排序算法一般都要依托一些高级一点的数据结构,这里就不再细说了。
1. 冒泡排序
1.1 冒泡排序-算法原理
1.2 冒泡排序-时间复杂度分析
1.3 冒泡排序-代码实现
2. 选择排序
2.1 选择排序-算法原理
2.2 选择排序-时间复杂度分析
2.3 选择排序-代码实现
3. 插入排序
3.1 插入排序-算法原理
3.2 插入排序-时间复杂度分析
3.3 插入排序-代码实现
4. 快速排序
4.1 快速排序-算法原理
4.2 快速排序-时间复杂度分析
4.3 快速排序-代码实现
5. 归并排序
5.1 归并排序-算法原理
5.2 归并排序-时间复杂度分析
5.3 归并排序-代码实现
6. 希尔排序
6.1 希尔排序-算法原理
6.2 希尔排序-时间复杂度分析
6.3 希尔排序-代码实现
1. 冒泡排序
算法原理
冒泡排序在所有排序算法中,属于比较基础的一种。它的原理就是通过遍历待排序元素列,依次比较相邻元素,按照一定的规则调整它们的顺序(如何复合规则,则继续遍历),直至排序完毕。
一般来说,这个算法都是用来针对数组排序,而且往往最终结果都是非降序排列的,因此狭义地来说,冒泡排序可以归纳为:
a. 比较相邻元素,若前者大于后者,则进行交换;
b. 对每一组相邻元素重复操作a,从第
1
1
1 对到第
n
−
1
n-1
n−1 对,此时,数组中最大的元素已经沉到数组最底部了;
c. 此时可以将最后一个元素抛开,针对前
n
−
1
n-1
n−1 个元素组成的数组继续执行操作a和b;
d. 持续上述操作,满足达到遍历轮数。
这里我们结合一个具体的例子来理解一下冒泡排序:有数组 A = { 5 , 4 , 3 , 2 , 1 } A={5,4,3,2,1} A={5,4,3,2,1},利用冒泡排序将其调整为非降序排列。
| 初始状态 | { 5 , 4 , 3 , 2 , 1 } {5,4,3,2,1} {5,4,3,2,1} |
|---|---|
| 第一轮排序 | 5 > 4 → { 4 , 5 , 3 , 2 , 1 } 5 > 3 → { 4 , 3 , 5 , 2 , 1 } 5 > 2 → { 4 , 3 , 2 , 5 , 1 } 5 > 1 → { 4 , 3 , 2 , 1 , 5 } 5>4rightarrow{4,5,3,2,1}\\5>3rightarrow{4,3,5,2,1}\\5>2rightarrow{4,3,2,5,1}\\5>1rightarrow{4,3,2,1,5} 5>4→{4,5,3,2,1}5>3→{4,3,5,2,1}5>2→{4,3,2,5,1}5>1→{4,3,2,1,5} |
第一轮排序结束之后,数组的最大元素一定沉到了数组的末尾,那么,接下来的第二轮排序只需要针对
{
4
,
3
,
2
,
1
}
{4,3,2,1}
{4,3,2,1} 进行即可,以此类推,第四轮排序结束之后,数组已是非降序。下面来看算法:
—————————-——
b
u
b
b
l
e
_
s
o
r
t
bubble_sort
bubble_sort——————————————
- 输入:待排序元素列 A [ 1 … n ] A[1dots n] A[1…n] 和数组长度
- 输出:非降序排列元素列(实际上这里的规则可以自定义,在对应的代码部分做好修改即可,但一般都是非降序数组)
- b u b b l e _ s o r t ( A [ 1 … n ] , n ) bubble_sort(A[1dots n],n) bubble_sort(A[1…n],n)
- 过程:
- 1. f o r i ← 1 t o n − 1 { hspace{1cm}1.space forspacespace ileftarrow1spacespace tospacespace n-1spacespace{ 1. for i←1 to n−1 {表示遍历的轮数,即一共遍历 n − 1 n-1 n−1 轮 } } }
- 2. f o r j ← 1 t o n − i − 1 { hspace{1cm}2.spacehspace{1cm}forspacespace jleftarrow1spacespace tospacespace n-i-1spacespace{ 2. for j←1 to n−i−1 {最大的元素渐渐沉到末尾,小的元素向上浮 } } }
- 3. i f A [ j ] > A [ j + 1 ] t h e n hspace{1cm}3.spacehspace{2cm}ifspacespace A[j]>A[j+1]spacespace then 3. if A[j]>A[j+1] then
- 4. t m p ← A [ j ] hspace{1cm}4.spacehspace{3cm}tmpleftarrow A[j] 4. tmp←A[j]
- 5. A [ j ] ← A [ j + 1 ] hspace{1cm}5.spacehspace{3cm}A[j]leftarrow A[j+1] 5. A[j]←A[j+1]
- 6. A [ j + 1 ] ← t m p hspace{1cm}6.spacehspace{3cm}A[j+1]leftarrow tmp 6. A[j+1]←tmp
- 7. e n d i f hspace{1cm}7.spacehspace{2cm}endspace if 7. end if
- 8. e n d f o r hspace{1cm}8.spacehspace{1cm}endspace for 8. end for
- 9. e n d f o r hspace{1cm}9.space endspace for 9. end for
————————————————————————————————
复杂度分析
最好情况:数组一开始就是非降序排列的,那么一趟扫描就可以完成排序,元素比较次数为
C
=
C
m
i
n
=
n
−
1
C=C_{min}=n-1
C=Cmin=n−1,记录移动次数
M
=
M
m
i
n
=
0
M=M_{min}=0
M=Mmin=0,因此,最好情况下的时间复杂度为
O
(
n
)
O(n)
O(n)。
最坏情况:例如上述例子,数组一开始是非升序排列的,那么需要进行
n
−
1
n-1
n−1 轮遍历,每轮遍历需要执行
n
−
i
(
1
⩽
i
⩽
n
−
1
)
n-ispace(1leqslant ileqslant n-1)
n−i (1⩽i⩽n−1) 次元素比较,有
C
=
C
m
a
x
=
n
(
n
−
1
)
2
=
O
(
n
2
)
C=C_{max}=frac{n(n-1)}{2}=O(n^2)
C=Cmax=2n(n−1)=O(n2);另外每次比较都伴随着记录的三次移动,又有
M
=
M
m
a
x
=
3
n
(
n
−
1
)
2
=
O
(
n
2
)
M=M_{max}=frac{3n(n-1)}{2}=O(n^2)
M=Mmax=23n(n−1)=O(n2),因此,最坏情况下的时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
综上,我们可以认为冒泡排序的平均时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
实现
C C C++
void bubble_sort(int A[], int n){
for(int i=0; i<n-1; i++){
for(int j=0; j<n-i-1; j++){
if(A[j] > A[j+1]){
int tmp = A[j];
A[j] = A[j+1];
A[j+1] = tmp;
}
}
}
}
P y t h o n Python Python
def bubble_sort(A, n):
for i in range(0, n-1):
for j in range(0, n-i-1):
if A[j] > A[j+1]:
tmp = A[j]
A[j] = A[j+1]
A[j+1] = tmp
return A
J a v a Java Java
public static void bubbleSort(int[] A, int n){
for(int i=0; i<n-1; i++){
for(int j=0; j<n-i-1; j++){
if(A[j] > A[j+1]){
int tmp = A[j];
A[j] = A[j+1];
A[j+1] = tmp;
}
}
}
}
| 表格分割线 |
|---|
2. 选择排序
算法原理
选择排序的基本思路比较直观(这里只了解基本排序排序,实际上可以借助树等数据结构进行改写),现在假设
A
[
1
…
n
]
A[1dots n]
A[1…n] 为一个有
n
n
n 个元素的数组,需要对其按非降序规则进行排序,那么我们可以先遍历数组,找到其中最小的元素,然后将其与
A
[
1
]
A[1]
A[1] 进行交换;然后遍历剩下的
n
−
1
n-1
n−1 个元素
(
A
[
2
…
n
]
)
(A[2dots n])
(A[2…n]) 中最小的元素,将其与
A
[
2
]
A[2]
A[2] 进行交换;重复操作直至完成
A
[
n
−
1
]
A[n-1]
A[n−1] 的交换,此时
A
[
n
]
A[n]
A[n] 中已经存储数组
A
[
1
…
n
]
A[1dots n]
A[1…n] 中最大的元素,即数组排序完毕。直接看算法:
—————————-——
s
e
l
e
c
t
i
o
n
_
s
o
r
t
selection_sort
selection_sort——————————————
- 输入:待排序数组 A [ 1 … n ] A[1dots n] A[1…n] 和数组长度
- 输出:非降序排列数组 A [ 1 … n ] A[1dots n] A[1…n]
- s e l e c t i o n _ s o r t ( A [ 1 … n ] , n ) selection_sort(A[1dots n],n) selection_sort(A[1…n],n)
- 过程:
- 1. f o r i ← 1 t o n − 1 { hspace{1cm}1.space forspacespace ileftarrow1spacespace tospacespace n-1spacespace{ 1. for i←1 to n−1 {依次找到前 n − 1 n-1 n−1 小的数组元素 } } }
- 2. k ← i hspace{1cm}2.spacehspace{1cm}kleftarrow i 2. k←i
- 3. f o r j ← i + 1 t o n { hspace{1cm}3.hspace{1cm}forspacespace jleftarrow i+1spacespace tospacespace nspacespace{ 3.for j←i+1 to n {查找第 i i i 小的元素 } } }
- 4. i f A [ j ] < A [ k ] t h e n k ← j hspace{1cm}4.spacehspace{2cm}ifspacespace A[j]<A[k]spacespace thenspacespace kleftarrow j 4. if A[j]<A[k] then k←j
- 5. e n d f o r hspace{1cm}5.spacehspace{1cm}endspace for 5. end for
- 6. i f k ≠ i t h e n hspace{1cm}6.spacehspace{1cm}ifspacespace kneq ispacespace then 6. if k=i then
- 7. t m p = A [ i ] hspace{1cm}7.spacehspace{2cm}tmp=A[i] 7. tmp=A[i]
- 8. A [ i ] = A [ k ] hspace{1cm}8.spacehspace{2cm}A[i]=A[k] 8. A[i]=A[k]
- 9. A [ k ] = t m p hspace{1cm}9.spacehspace{2cm}A[k]=tmp 9. A[k]=tmp
- 10. e n d i f hspace{0.85cm}10.spacehspace{1cm}endspace if 10. end if
- 11. e n d f o r hspace{0.85cm}11.space endspace for 11. end for
————————————————————————————————
复杂度分析
这里我们将最好情况和最坏情况放在一起看,易知该算法执行的元素比较次数为
∑
i
=
1
n
−
1
(
n
−
i
)
=
(
n
−
1
)
+
(
n
−
2
)
+
⋯
+
1
=
∑
i
=
1
n
−
1
i
=
n
(
n
−
1
)
2
sum_{i=1}^{n-1}(n-i)=(n-1)+(n-2)+cdots+1=sum_{i=1}^{n-1}i=frac{n(n-1)}{2}
∑i=1n−1(n−i)=(n−1)+(n−2)+⋯+1=∑i=1n−1i=2n(n−1)
也可以看出元素交换的次数介于
0
∼
n
−
1
0sim n-1
0∼n−1 之间,由于每次交换都伴随着记录的三次移动,因此可知记录移动次数介于
0
∼
3
(
n
−
1
)
0sim3(n-1)
0∼3(n−1) 之间。
综上,基本选择排序算法的时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
实现
C C C++
void selection_sort(int A[], int n){
for(int i=0; i<n-1; i++){
int k = i;
for(int j=i+1; j<n; j++){
if(A[j] < A[k]) k = j;
}
if(k != i){
int tmp = A[i];
A[i] = A[k];
A[k] = tmp;
}
}
}
P y t h o n Python Python
def selection_sort(A, n):
for i in range(0, n-1):
k = i
for j in range(i+1, n):
if A[j] < A[k]:
k = j
if k != i:
tmp = A[i]
A[i] = A[k]
A[k] = tmp
return A
J a v a Java Java
public static void selectionSort(int[] A, int n){
for(int i=0; i<n-1; i++){
int k = i;
for(int j=i+1; j<n; j++){
if(A[j] < A[k]) k = j;
}
if(k != i){
int tmp = A[i];
A[i] = A[k];
A[k] = tmp;
}
}
}
| 表格分割线 |
|---|
3. 插入排序
算法原理
插入排序依赖于已经有序的元素序列,它的核心要义就是——在已经排序完毕的元素序列中插入指定元素,并且插入元素之后不破坏原有的排列规则。这里是直接插入排序的算法思路:
从大小为
1
1
1 的子数组
A
[
1
]
A[1]
A[1] 开始,显然该数组已经排序完毕;
接下来需要插入
A
[
2
]
A[2]
A[2]:比较
A
[
1
]
A[1]
A[1] 和
A
[
2
]
A[2]
A[2] 的大小,根据排序规则选择将
A
[
2
]
A[2]
A[2] 插入到
A
[
1
]
A[1]
A[1] 的前面或者后面;
重复插入操作,那么在第
i
i
i 次操作中,我们需要将
A
[
i
]
A[i]
A[i] 插入到已经排序完毕的子数组
A
[
1
…
i
−
1
]
A[1dots i-1]
A[1…i−1] 中的合适位置:遍历第
i
−
1
∼
1
i-1sim1
i−1∼1 号元素,每次都将
A
[
i
]
A[i]
A[i] 同当前位置的元素进行比较。遍历的每一步,元素都会被移动到序号更高的位置上,这样重复比较操作和移位操作直至找到一个小于
A
[
i
]
A[i]
A[i] 的元素,或者已经排序完毕的数组被全部遍历完,此时,
A
[
i
]
A[i]
A[i] 就已经被插入到合适的位置上了。下面我们根据一个例子来简单理解一下该算法执行的过程:
| 初始值排序 | { 12 } 15 , 9 , 20 , 6 , 31 , 24 {12}hspace{1cm}15,9,20,6,31,24 {12}15,9,20,6,31,24 |
|---|---|
| 第一次插入排序 | { 12 , 15 } 9 , 20 , 6 , 31 , 24 {12,15}hspace{1cm}9,20,6,31,24 {12,15}9,20,6,31,24 |
| 第二次插入排序 | { 9 , 12 , 15 } 20 , 6 , 31 , 24 {9,12,15}hspace{1cm}20,6,31,24 {9,12,15}20,6,31,24 |
| 第三次插入排序 | { 9 , 12 , 15 , 20 } 6 , 31 , 24 {9,12,15,20}hspace{1cm}6,31,24 {9,12,15,20}6,31,24 |
| 第四次插入排序 | { 6 , 9 , 12 , 15 , 20 } 31 , 24 {6,9,12,15,20}hspace{1cm}31,24 {6,9,12,15,20}31,24 |
| 第五次插入排序 | { 6 , 9 , 12 , 15 , 20 , 31 } 24 {6,9,12,15,20,31}hspace{1cm}24 {6,9,12,15,20,31}24 |
| 第六次插入排序 | { 6 , 9 , 12 , 15 , 20 , 24 , 31 } {6,9,12,15,20,24,31} {6,9,12,15,20,24,31} |
算法具体步骤:
—————————-——
i
n
s
e
r
t
i
o
n
_
s
o
r
t
insertion_sort
insertion_sort——————————————
- 输入:待排序数组 A [ 1 … n ] A[1dots n] A[1…n] 和数组长度
- 输出:非降序排列数组 A [ 1 … n ] A[1dots n] A[1…n]
- i n s e r t i o n _ s o r t ( A [ 1 … n ] , n ) insertion_sort(A[1dots n],n) insertion_sort(A[1…n],n)
- 过程:
- 1. f o r i ← 2 t o n hspace{1cm}1.space forspacespace ileftarrow2spacespace tospacespace n 1. for i←2 to n
- 2. x ← A [ i ] hspace{1cm}2.spacehspace{1cm}xleftarrow A[i] 2. x←A[i]
- 3. j ← i − 1 hspace{1cm}3.spacehspace{1cm}jleftarrow i-1 3. j←i−1
- 4. w h i l e ( j > 0 ) a n d ( A [ j ] > x ) { hspace{1cm}4.hspace{1cm}whilespacespace(j>0)spacespace andspacespace (A[j]>x)spacespace{ 4.while (j>0) and (A[j]>x) {查找第 i i i 个元素的插入位置 } } }
- 5. A [ j + 1 ] ← A [ j ] hspace{1cm}5.spacehspace{2cm}A[j+1]leftarrow A[j] 5. A[j+1]←A[j]
- 6. j ← j − 1 hspace{1cm}6.spacehspace{2cm}jleftarrow j-1 6. j←j−1
- 7. e n d w h i l e hspace{1cm}7.spacehspace{1cm}endspace while 7. end while
- 8. A [ j + 1 ] ← x hspace{1cm}8.spacehspace{1cm}A[j+1]leftarrow x 8. A[j+1]←x
- 9. e n d f o r hspace{1cm}9.space endspace for 9. end for
————————————————————————————————
复杂度分析
易知,元素比较的次数取决于输入元素的顺序。因此,
在最好情况下,数组已按非降序排列,元素的比较次数最少,为
n
−
1
n-1
n−1 次;
在最坏情况下,数组按降序排列,并且所有元素各不相同,元素的比较次数最大,为
∑
i
=
2
n
(
i
−
1
)
=
∑
i
=
1
n
−
1
i
=
n
(
n
−
1
)
2
sum_{i=2}^n(i-1)=sum_{i=1}^{n-1}i=frac{n(n-1)}{2}
∑i=2n(i−1)=∑i=1n−1i=2n(n−1)
综上,直接插入排序算法的平均时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
实现
C C C++
void insertion_sort(int A[], int n){
for(int i=1; i<n; i++){
int x = A[i], j = i-1;
while(j>=0 && A[j]>x){
A[j+1] = A[j];
j--;
}
A[j+1] = x;
}
}
P y t h o n Python Python
def insertion_sort(A, n):
for i in range(1, n):
x = A[i]
j = i-1
while (j>=0) and (A[j]>x):
A[j+1] = A[j]
j -= 1
A[j+1] = x
return A
J a v a Java Java
public static void insertionSort(int[] A, int n){
for(int i=1; i<n; i++){
int x = A[i], j = i-1;
while(j>=0 && A[j]>x){
A[j+1] = A[j];
j--;
}
A[j+1] = x;
}
}
| 表格分割线 |
|---|
4. 快速排序
算法原理
快速排序算法,实际上就是对冒泡排序的改进,它的核心思路就是先通过一次排序(遍历)将待排序元素序列 A A A 分割成两个独立的子元素序列 A 1 , A 2 A_1,A_2 A1,A2,其中 A 1 A_1 A1 中所有元素针对 A 2 A_2 A2 中所有元素都符合给定排序规则,然后对 A 1 , A 2 A_1,A_2 A1,A2 重复上述操作,易知整个排序过程都可以递归进行,根据上述原理我们可以得到如下排序流程:
- ( 1 ) (1) (1) 设置分割点,用来分割待排序元素序列
- ( 2 ) (2) (2) 结合分割点和排序规则将待排序元素序列分割为两个子序列
- ( 3 ) (3) (3) 针对两个子序列分别执行操作:设置分割点,结合分割点和排序规则将子序列继续分割
- ( 4 ) (4) (4) 重复上述操作,通过递归先将左侧部分排好序,再将右侧部分排好序,最终得到排序完毕的元素序列
可见快速排序算法主要借助的就是“分治”的思想。那么,如何“分”,就是该算法的重要前提:
划分算法:设
A
[
1
…
n
]
A[1dots n]
A[1…n] 是一个实数数组,要求将其整理为非降序排列。
我们先来设置分割点
r
e
f
ref
ref,一般来说都会默认为数组的第一个元素,即
r
e
f
=
A
[
1
]
ref=A[1]
ref=A[1]。下面就需要调整数组顺序,使得小于或等于
r
e
f
ref
ref 的元素都排在它前面,所有大于
r
e
f
ref
ref 的元素都排在它的后面。
例如有
e
x
=
{
5
,
3
,
9
,
2
,
7
,
1
,
8
}
ex={5,3,9,2,7,1,8}
ex={5,3,9,2,7,1,8},再执行完划分算法后就要得到
e
x
=
{
1
,
3
,
2
,
5
,
7
,
9
,
8
}
ex={1,3,2,5,7,9,8}
ex={1,3,2,5,7,9,8}。但是,这又是如何得到的呢?实际上有很多策略都可以实现划分,但是上述的例子中,采取的是如下算法:
- 输入:数组 A [ l o w , h i g h ] A[low,space high] A[low, high]
- 输出:新数组 A A A 和 r e f = A [ l o w ] ref=A[low] ref=A[low] 的在新数组中的位置
- 1. i ← l o w hspace{1cm}1.space ileftarrow low 1. i←low
- 2. r e f ← A [ l o w ] hspace{1cm}2.space refleftarrow A[low] 2. ref←A[low]
- 3. f o r j ← l o w + 1 t o h i g h hspace{1cm}3.space forspacespace jleftarrow low+1spacespace tospacespace high 3. for j←low+1 to high
- 4. i f A [ j ] ⩽ r e f t h e n hspace{1cm}4.spacehspace{1cm}ifspacespace A[j]leqslant refspacespace then 4. if A[j]⩽ref then
- 5. i ← i + 1 hspace{1cm}5.spacehspace{2cm}ileftarrow i+1 5. i←i+1
- 6. i f i ≠ j t h e n s w a p ( A [ i ] , A [ j ] ) hspace{1cm}6.spacehspace{2cm}ifspacespace ineq jspacespace thenspacespace swap(A[i],A[j]) 6. if i=j then swap(A[i],A[j])
- 7. e n d i f hspace{1cm}7.spacehspace{1cm}endspace if 7. end if
- 8. e n d f o r hspace{1cm}8.space endspace for 8. end for
- 9. s w a p ( A [ l o w ] , A [ i ] ) hspace{1cm}9.space swap(A[low],A[i]) 9. swap(A[low],A[i])
- 10. w ← i hspace{0.85cm}10.space wleftarrow i 10. w←i
- 11. r e t u r n A a n d w hspace{0.85cm}11.space returnspace Aspace andspace w 11. return A and w
上述算法在执行过程中主要利用 i , j i,j i,j 指针,先将其设置为 i = l o w , j = l o w + 1 i=low,j=low+1 i=low,j=low+1,然后借助 f o r for for 循环遍历数组, f o r for for 循环执行结束后得到:
- A [ l o w ] = r e f A[low]=ref A[low]=ref
- A [ k ] ⩽ r e f , l o w ⩽ k ⩽ i A[k]leqslant ref,space lowleqslant kleqslant i A[k]⩽ref, low⩽k⩽i
- A [ k ] > r e f , i < k ⩽ j A[k]>ref,space i<kleqslant j A[k]>ref, i<k⩽j
最后再将 A [ i ] A[i] A[i] 与 r e f ref ref 交换,这样就得到了我们期待的新数组。下面我们根据一个例子来具体看一下划分算法的执行步骤:
| 初始值情况 | { 5 , 7 , 1 , 6 , 4 , 8 , 3 , 2 } {5,7,1,6,4,8,3,2} {5,7,1,6,4,8,3,2} 此时有 l o w = 1 , h i g h = 8 , r e f = 5 low=1,high=8,ref=5 low=1,high=8,ref=5 |
|---|---|
| ( 1 ) (1) (1) | i = l o w , A [ i ] = 5 ; j = l o w + 1 , A [ j ] = 7 i=low,A[i]=5;space j=low+1,A[j]=7 i=low,A[i]=5; j=low+1,A[j]=7 |
| ( 2 ) (2) (2) | j = 3 j=3 j=3 时 A [ 3 ] = 1 ⩽ r e f = 5 ⇒ i = 2 ≠ j ⇒ { 5 , 1 , 7 , 6 , 4 , 8 , 3 , 2 } A[3]=1leqslant ref=5Rightarrow i=2neq jRightarrow{5,1,7,6,4,8,3,2} A[3]=1⩽ref=5⇒i=2=j⇒{5,1,7,6,4,8,3,2} |
| ( 3 ) (3) (3) | j = 5 j=5 j=5 时 A [ 5 ] = 4 ⩽ r e f = 5 ⇒ i = 3 ≠ j ⇒ { 5 , 1 , 4 , 6 , 7 , 8 , 3 , 2 } A[5]=4leqslant ref=5Rightarrow i=3neq jRightarrow{5,1,4,6,7,8,3,2} A[5]=4⩽ref=5⇒i=3=j⇒{5,1,4,6,7,8,3,2} |
| ( 4 ) (4) (4) | j = 7 j=7 j=7 时 A [ 7 ] = 3 ⩽ r e f = 5 ⇒ i = 4 ≠ j ⇒ { 5 , 1 , 4 , 3 , 7 , 8 , 6 , 2 } A[7]=3leqslant ref=5Rightarrow i=4neq jRightarrow{5,1,4,3,7,8,6,2} A[7]=3⩽ref=5⇒i=4=j⇒{5,1,4,3,7,8,6,2} |
| ( 5 ) (5) (5) | j = 8 j=8 j=8 时 A [ 8 ] = 2 ⩽ r e f = 5 ⇒ i = 5 ≠ j ⇒ { 5 , 1 , 4 , 3 , 2 , 8 , 6 , 7 } A[8]=2leqslant ref=5Rightarrow i=5neq jRightarrow{5,1,4,3,2,8,6,7} A[8]=2⩽ref=5⇒i=5=j⇒{5,1,4,3,2,8,6,7} |
| ( 6 ) (6) (6) | j = 8 = h i g h ⇒ j=8=highRightarrow j=8=high⇒ f o r for for 循环停止 |
| ( 7 ) (7) (7) | s w a p ( A [ l o w ] , A [ i ] ) ⇒ { 2 , 1 , 4 , 3 , 5 , 8 , 6 , 7 } swap(A[low],A[i])Rightarrow{2,1,4,3,5,8,6,7} swap(A[low],A[i])⇒{2,1,4,3,5,8,6,7} |
| ( 8 ) (8) (8) | 算法执行完毕 |
最后注意到上述算法仅仅用到一个额外变量来存储它的局部变量,因此该划分算法的空间复杂度为 Θ ( 1 ) Theta(1) Θ(1)。下面,我们就可以结合划分算法,借助递归调用完成快速排序的算法设计:
—————————-—— q u i c k _ s o r t quick_sort quick_sort——————————————
- 输入:待排序数组 A [ 1 … n ] A[1dots n] A[1…n] 和数组起始下标索引
- 输出:非降序排列数组 A [ 1 … n ] A[1dots n] A[1…n]
- q u i c k _ s o r t ( A [ 1 … n ] , 1 , n ) quick_sort(A[1dots n],1,n) quick_sort(A[1…n],1,n)
- 过程: q u i c k _ s o r t ( A , l o w , h i g h ) quick_sort(A,low,high) quick_sort(A,low,high)
- 1. i f l o w < h i g h t h e n hspace{1cm}1.space ifspacespace low<highspacespace then 1. if low<high then
- 2. i ← l o w hspace{1cm}2.spacehspace{1cm} ileftarrow low 2. i←low
- 3. r e f ← A [ l o w ] hspace{1cm}3.spacehspace{1cm} refleftarrow A[low] 3. ref←A[low]
- 4. f o r j ← l o w + 1 t o h i g h hspace{1cm}4.spacehspace{1cm} forspacespace jleftarrow low+1spacespace tospacespace high 4. for j←low+1 to high
- 5. i f A [ j ] ⩽ r e f t h e n hspace{1cm}5.spacehspace{2cm}ifspacespace A[j]leqslant refspacespace then 5. if A[j]⩽ref then
- 6. i ← i + 1 hspace{1cm}6.spacehspace{3cm}ileftarrow i+1 6. i←i+1
- 7. i f i ≠ j t h e n s w a p ( A [ i ] , A [ j ] ) hspace{1cm}7.spacehspace{3cm}ifspacespace ineq jspacespace thenspacespace swap(A[i],A[j]) 7. if i=j then swap(A[i],A[j])
- 8. e n d i f hspace{1cm}8.spacehspace{2cm}endspace if 8. end if
- 9. e n d f o r hspace{1cm}9.spacehspace{1cm} endspace for 9. end for
- 10. s w a p ( A [ l o w ] , A [ i ] ) hspace{0.85cm}10.spacehspace{1cm} swap(A[low],A[i]) 10. swap(A[low],A[i])
- 11. w ← i hspace{0.85cm}11.spacehspace{1cm} wleftarrow i 11. w←i
- 12. q u i c k _ s o r t ( A , l o w , w − 1 ) hspace{0.85cm}12.spacehspace{1cm} quick_sort(A,low,w-1) 12. quick_sort(A,low,w−1)
- 13. q u i c k _ s o r t ( A , w + 1 , h i g h ) hspace{0.85cm}13.spacehspace{1cm} quick_sort(A,w+1,high) 13. quick_sort(A,w+1,high)
- 14. e n d i f hspace{0.85cm}14.space endspace if 14. end if
————————————————————————————————
复杂度分析
最坏情况
对于算法
q
u
i
c
k
_
s
o
r
t
(
A
,
l
o
w
,
h
i
g
h
)
quick_sort(A,low,high)
quick_sort(A,low,high) 的每次调用,
r
e
f
=
A
[
l
o
w
]
ref=A[low]
ref=A[low] 都是数组中的最小值元素,那么仅仅存在一个有效的递归调用,而另一个调用就将作用在空数组上,即算法是由调用
q
u
i
c
k
_
s
o
r
t
(
A
,
1
,
n
)
quick_sort(A,1,n)
quick_sort(A,1,n) 开始,下一步的两个递归调用分别是
q
u
i
c
k
_
s
o
r
t
(
A
,
1
,
0
)
quick_sort(A,1,0)
quick_sort(A,1,0) 和
q
u
i
c
k
_
s
o
r
t
(
A
,
2
,
n
)
quick_sort(A,2,n)
quick_sort(A,2,n),其中,第一个就是无效调用。
因此,若输入的待排序数组已经是非降序排列的,最坏情况就出现了。简单来说,下面对于
q
u
i
c
k
_
s
o
r
t
(
A
,
l
o
w
,
h
i
g
h
)
quick_sort(A,low,high)
quick_sort(A,low,high) 过程的
n
n
n 次调用将发生
q
u
i
c
k
_
s
o
r
t
(
A
,
1
,
n
)
,
q
u
i
c
k
_
s
o
r
t
(
A
,
2
,
n
)
,
…
,
q
u
i
c
k
_
s
o
r
t
(
A
,
n
,
n
)
quick_sort(A,1,n),space quick_sort(A,2,n),dots,space quick_sort(A,n,n)
quick_sort(A,1,n), quick_sort(A,2,n),…, quick_sort(A,n,n)。
由于对于输入大小为
j
j
j 的元素,划分算法执行的元素比较次数为
j
−
1
j-1
j−1,因此在最坏情况下,算法
q
u
i
c
k
_
s
o
r
t
(
A
,
l
o
w
,
h
i
g
h
)
quick_sort(A,low,high)
quick_sort(A,low,high) 执行的元素总比较次数是
(
n
−
1
)
+
(
n
−
2
)
+
⋯
+
1
+
0
=
n
(
n
−
1
)
2
=
Θ
(
n
2
)
(n-1)+(n-2)+cdots+1+0=frac{n(n-1)}{2}=Theta(n^2)
(n−1)+(n−2)+⋯+1+0=2n(n−1)=Θ(n2)
但是我们要注意一点,如果我们总是在线性时间内选择中项作为分割点
r
e
f
ref
ref,最坏情况下的运行时间可以被改进为
Θ
(
n
log
n
)
Theta(nlog n)
Θ(nlogn),主要是因为这么划分元素是高度平衡的,而在这种情况下,两个递归调用具有几乎相同数目的元素,进而得到计算比较次数的递推式:
C
(
n
)
=
{
0
i
f
n
=
1
2
C
(
n
2
)
+
Θ
(
n
)
i
f
n
>
1
C(n)=begin{cases}0hspace{1cm}ifspacespace n=1\\2C(frac{n}{2})+Theta(n)hspace{1cm}ifspacespace n>1end{cases}
C(n)=⎩⎪⎨⎪⎧0if n=12C(2n)+Θ(n)if n>1
最终求得
C
(
n
)
=
Θ
(
n
log
n
)
C(n)=Theta(nlog n)
C(n)=Θ(nlogn),但是找出中项的算法对时间复杂度的影响不可控,因而不值得与
q
u
i
c
k
_
s
o
r
t
(
A
,
l
o
w
,
h
i
g
h
)
quick_sort(A,low,high)
quick_sort(A,low,high) 算法配合使用。
平均情况
我们必须承认最坏情况会在算法执行时发生,但是它同时也属于极端情况,即在实际情况下是很少发生的,因此用最坏情况下的算法运行时间来界定时间复杂度很不合理。下面来看看平均情况:
为了便于理解,我们假定输入数据是互不相同的(这是不失一般性的,因为算法的性能与输入数据值是无关的,有关系的是它们的相对次序),不如更进一步,我们直接假设进行排序的元素是前
n
n
n 个正整数
1
,
2
,
…
,
n
1,2,dots,n
1,2,…,n。
在分析算法的平均性能的过程中,我们必须高度关注输入数据的概率分布,这里采用简化分析的方法,就假定元素的每个排列的出现是等可能的,即对于
1
,
2
,
…
,
n
1,2,dots,n
1,2,…,n 的
n
!
n!
n! 种排列情况来说,每一个排列的出现是等可能的,这一点主要是为了确保数组中的每个数被选作
r
e
f
ref
ref 的可能性是一样的,即数组
A
A
A 中任意元素被选为分割点的概率都是
1
n
frac{1}{n}
n1。设
C
(
n
)
C(n)
C(n) 为对于大小为
n
n
n 的输入数据,
q
u
i
c
k
_
s
o
r
t
(
A
,
l
o
w
,
h
i
g
h
)
quick_sort(A,low,high)
quick_sort(A,low,high) 算法所执行的平均比较次数,结合上述假设和算法的具体设计,得到
C
(
n
)
=
(
n
−
1
)
+
1
n
∑
w
=
1
n
(
C
(
w
−
1
)
+
C
(
n
−
w
)
)
C(n)=(n-1)+frac{1}{n}sum_{w=1}^nbig(C(w-1)+C(n-w)big)
C(n)=(n−1)+n1∑w=1n(C(w−1)+C(n−w))
∵
∑
w
=
1
n
C
(
n
−
w
)
=
C
(
n
−
1
)
+
C
(
n
−
2
)
+
⋯
+
C
(
0
)
=
∑
w
=
1
n
C
(
w
−
1
)
becausesum_{w=1}^nC(n-w)=C(n-1)+C(n-2)+cdots+C(0)=sum_{w=1}^nC(w-1)
∵∑w=1nC(n−w)=C(n−1)+C(n−2)+⋯+C(0)=∑w=1nC(w−1)
∴
C
(
n
)
=
(
n
−
1
)
+
2
n
∑
w
=
1
n
C
(
w
−
1
)
therefore C(n)=(n-1)+frac{2}{n}sum_{w=1}^nC(w-1)
∴C(n)=(n−1)+n2∑w=1nC(w−1)
⇒
n
C
(
n
)
=
n
(
n
−
1
)
+
2
∑
w
=
1
n
C
(
w
−
1
)
Rightarrow nC(n)=n(n-1)+2sum_{w=1}^nC(w-1)
⇒nC(n)=n(n−1)+2∑w=1nC(w−1)
⇒
(
n
−
1
)
C
(
n
−
1
)
=
(
n
−
1
)
(
n
−
2
)
+
2
∑
w
=
1
n
−
1
C
(
w
−
1
)
Rightarrow (n-1)C(n-1)=(n-1)(n-2)+2sum_{w=1}^{n-1}C(w-1)
⇒(n−1)C(n−1)=(n−1)(n−2)+2∑w=1n−1C(w−1)
⇒
C
(
n
)
n
+
1
=
C
(
n
−
1
)
n
+
2
(
n
−
1
)
n
(
n
+
1
)
=
D
(
n
)
Rightarrowfrac{C(n)}{n+1}=frac{C(n-1)}{n}+frac{2(n-1)}{n(n+1)}=D(n)
⇒n+1C(n)=nC(n−1)+n(n+1)2(n−1)=D(n)
⇒
D
(
n
)
=
D
(
n
−
1
)
+
2
(
n
−
1
)
n
(
n
+
1
)
a
n
d
D
(
1
)
=
0
Rightarrow D(n)=D(n-1)+frac{2(n-1)}{n(n+1)}spacespace andspacespace D(1)=0
⇒D(n)=D(n−1)+n(n+1)2(n−1) and D(1)=0
⇒
D
(
n
)
=
2
∑
j
=
1
n
j
−
1
j
(
j
+
1
)
Rightarrow D(n)=2sum_{j=1}^nfrac{j-1}{j(j+1)}
⇒D(n)=2∑j=1nj(j+1)j−1
=
2
∑
j
=
1
n
2
j
+
1
−
2
∑
j
=
1
n
1
j
hspace{1.32cm}=2sum_{j=1}^nfrac{2}{j+1}-2sum_{j=1}^nfrac{1}{j}
=2∑j=1nj+12−2∑j=1nj1
=
4
∑
j
=
2
n
+
1
1
j
−
2
∑
j
=
1
n
1
j
hspace{1.32cm}=4sum_{j=2}^{n+1}frac{1}{j}-2sum_{j=1}^nfrac{1}{j}
=4∑j=2n+1j1−2∑j=1nj1
=
2
∑
j
=
1
n
1
j
−
4
n
n
+
1
hspace{1.32cm}=2sum_{j=1}^nfrac{1}{j}-frac{4n}{n+1}
=2∑j=1nj1−n+14n
=
2
ln
n
−
Θ
(
1
)
hspace{1.32cm}=2ln n-Theta(1)
=2lnn−Θ(1)
=
2
log
e
log
n
−
Θ
(
1
)
hspace{1.32cm}=frac{2}{log e}log n-Theta(1)
=loge2logn−Θ(1)
≈
1.44
log
n
hspace{1.32cm}approx1.44log n
≈1.44logn
⇒
C
(
n
)
=
(
n
+
1
)
D
(
n
)
≈
1.44
n
log
n
Rightarrow C(n)=(n+1)D(n)approx1.44nlog n
⇒C(n)=(n+1)D(n)≈1.44nlogn
综上,我们可以得到 q u i c k _ s o r t quick_sort quick_sort 算法的时间复杂度为 Θ ( n log n ) Theta(nlog n) Θ(nlogn)。
实现
C C C++
void quick_sort(int A[], int low, int high){
if(low < high){
int i = low, ref = A[low];
for(int j=low+1; j<=high; j++){
if(A[j] <= ref){
i++;
if(i != j){
int tmp_0 = A[i];
A[i] = A[j];
A[j] = tmp_0;
}
}
}
int tmp_1 = A[low];
A[low] = A[i];
A[i] = tmp_1;
int w = i;
quick_sort(A, low, w-1);
quick_sort(A, w+1, high);
}
}
P y t h o n Python Python
def quick_sort(A, low, high):
if low < high:
i, ref = low, A[low]
for j in range(low+1, high+1):
if A[j] <= ref:
i += 1
if i != j:
tmp_0 = A[i]
A[i] = A[j]
A[j] = tmp_0
tmp_1 = A[low]
A[low] = A[i]
A[i] = tmp_1
w = i
quick_sort(A, low, w-1)
quick_sort(A, w+1, high)
return A
J a v a Java Java
public static void quickSort(int[] A, int low, int high){
if(low < high){
int i = low, ref = A[low];
for(int j=low+1; j<=high; j++){
if(A[j] <= ref){
i++;
if(i != j){
int tmp_0 = A[i];
A[i] = A[j];
A[j] = tmp_0;
}
}
}
int tmp_1 = A[low];
A[low] = A[i];
A[i] = tmp_1;
int w = i;
quickSort(A, low, w-1);
quickSort(A, w+1, high);
}
}
| 表格分割线 |
|---|
5. 归并排序
算法原理
归并排序算法是建立在归并操作上的一种有效的排序算法,该算法是分治思想设计算法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。在学习该算法之前,我们先来看一下何为归并操作:
现在假设有一个数组
A
[
1
…
m
]
,
p
,
q
,
r
A[1dots m],p,q,r
A[1…m],p,q,r 为其三个索引,并有
1
⩽
p
⩽
q
<
r
⩽
m
1leqslant pleqslant q<rleqslant m
1⩽p⩽q<r⩽m,两个子数组
A
[
p
…
q
]
A[pdots q]
A[p…q] 和
A
[
q
+
1
…
r
]
A[q+1dots r]
A[q+1…r] 都按升序排列,合并这两个数组的过程,就是重新安排
A
A
A 中元素的位置,使得子数组
A
[
p
…
r
]
A[pdots r]
A[p…r] 也按升序排列。算法具体思路如下:
使用两个指针
s
,
t
s,t
s,t,在初始状态下,
s
s
s 指向
A
[
p
]
A[p]
A[p],
t
t
t 指向
A
[
q
+
1
]
A[q+1]
A[q+1],再利用一个空数组
B
[
p
…
r
]
B[pdots r]
B[p…r] 作为暂存器。每一次比较元素
A
[
s
]
A[s]
A[s] 和
A
[
t
]
A[t]
A[t],将小的元素添加到暂存器中,若相同则添加
A
[
s
]
A[s]
A[s],然后再更新指针:若
A
[
s
]
⩽
A
[
t
]
A[s]leqslant A[t]
A[s]⩽A[t],则
s
s
s+=
1
1
1,否则
t
t
t+=
1
1
1。当条件
s
=
q
+
1
s=q+1
s=q+1 或者
t
=
r
+
1
t=r+1
t=r+1 满足时停止,若满足条件一,则把数组
A
[
t
…
r
]
A[tdots r]
A[t…r] 中剩余的元素添加至
B
B
B 中;若满足条件二,则把数组
A
[
s
…
q
]
A[sdots q]
A[s…q] 中剩余的元素添加至
B
B
B 中,最后再将暂存器数组
B
[
p
…
r
]
B[pdots r]
B[p…r] 复制回
A
[
p
…
r
]
A[pdots r]
A[p…r]。实际上,该思路的核心就是同时遍历两个子数组,在比较之后将每个元素一一装到暂存器中,下面看伪代码:
- 输入:数组 A [ 1 … m ] A[1dots m] A[1…m] 和其三个索引 p , q , r , 1 ⩽ p ⩽ q < r ⩽ m p,q,r,1leqslant pleqslant q<rleqslant m p,q,r,1⩽p⩽q<r⩽m,两个子数组 A [ p … q ] A[pdots q] A[p…q] 和 A [ q + 1 … r ] A[q+1dots r] A[q+1…r] 各自按升序排列。
- 输出:将子数组 A [ p … q ] A[pdots q] A[p…q] 和 A [ q + 1 … r ] A[q+1dots r] A[q+1…r] 合并为 A [ p … r ] A[pdots r] A[p…r]
- 1. c o m m e n t : B [ p … r ] hspace{1cm}1.space comment:B[pdots r] 1. comment:B[p…r] 是一个辅助数组(暂存器)
- 2. s ← p ; t ← q + 1 ; k ← p hspace{1cm}2.space sleftarrow pspace;space tleftarrow q+1space;space kleftarrow p 2. s←p ; t←q+1 ; k←p
- 3. w h i l e s ⩽ q a n d t ⩽ r hspace{1cm}3.space whilespacespace sleqslant qspacespace andspacespace tleqslant r 3. while s⩽q and t⩽r
- 4. i f A [ s ] ⩽ A [ t ] t h e n hspace{1cm}4.hspace{1cm}ifspacespace A[s]leqslant A[t]spacespace then 4.if A[s]⩽A[t] then
- 5. B [ k ] ← A [ s ] hspace{1cm}5.hspace{2cm}B[k]leftarrow A[s] 5.B[k]←A[s]
- 6. s ← s + 1 hspace{1cm}6.hspace{2cm}sleftarrow s+1 6.s←s+1
- 7. e l s e hspace{1cm}7.hspace{1cm}else 7.else
- 8. B [ k ] ← A [ t ] hspace{1cm}8.hspace{2cm}B[k]leftarrow A[t] 8.B[k]←A[t]
- 9. t ← t + 1 hspace{1cm}9.hspace{2cm}tleftarrow t+1 9.t←t+1
- 10. e n d i f hspace{0.85cm}10.hspace{1cm}endspace if 10.end if
- 11. k ← k + 1 hspace{0.85cm}11.spacehspace{1cm}kleftarrow k+1 11. k←k+1
- 12. e n d w h i l e hspace{0.85cm}12.space endspace while 12. end while
- 13. i f s = q + 1 t h e n B [ k … r ] ← A [ t … r ] hspace{0.85cm}13.space ifspacespace s=q+1spacespace thenspacespace B[kdots r]leftarrow A[tdots r] 13. if s=q+1 then B[k…r]←A[t…r]
- 14. e l s e B [ k … r ] ← A [ s … q ] hspace{0.85cm}14.space elsespacespace B[kdots r]leftarrow A[sdots q] 14. else B[k…r]←A[s…q]
- 15. e n d i f hspace{0.85cm}15.space endspace if 15. end if
- 16. A [ p … r ] ← B [ p … r ] hspace{0.85cm}16.space A[pdots r]leftarrow B[pdots r] 16. A[p…r]←B[p…r]
了解了归并操作,下面我们就可以来看一下归并排序算法的具体思路了。
假设有待排序数组
A
[
1
…
8
]
=
{
9
,
4
,
5
,
2
,
1
,
7
,
4
,
6
}
A[1dots8]={9,4,5,2,1,7,4,6}
A[1…8]={9,4,5,2,1,7,4,6},现在开始合并排序
m
e
r
g
e
_
s
o
r
t
(
A
,
1
,
8
)
merge_sort(A,1,8)
merge_sort(A,1,8),调用该算法会引起一个隐含二叉树所表示的一系列递归调用,树的每个结点由上下两个数组组成,上面的数组是调用算法的输入,下面的数组则是调用算法的输出,换句话说,顶端数组是“分”后的待排序数组,底端数组是“治”后“再作组合”的数组。二叉树的每个边用表示控制流的两个相向的边取代,边上的标号指明这些递归调用发生的次序,显然,这个调用链顺序为:访问根、左子树和右子树,但是计算顺序略有不同:左子树、右子树、根。为了实现该算法,我们需要用一个栈来存储每次调用过程生成的局部数据。下面是图示:
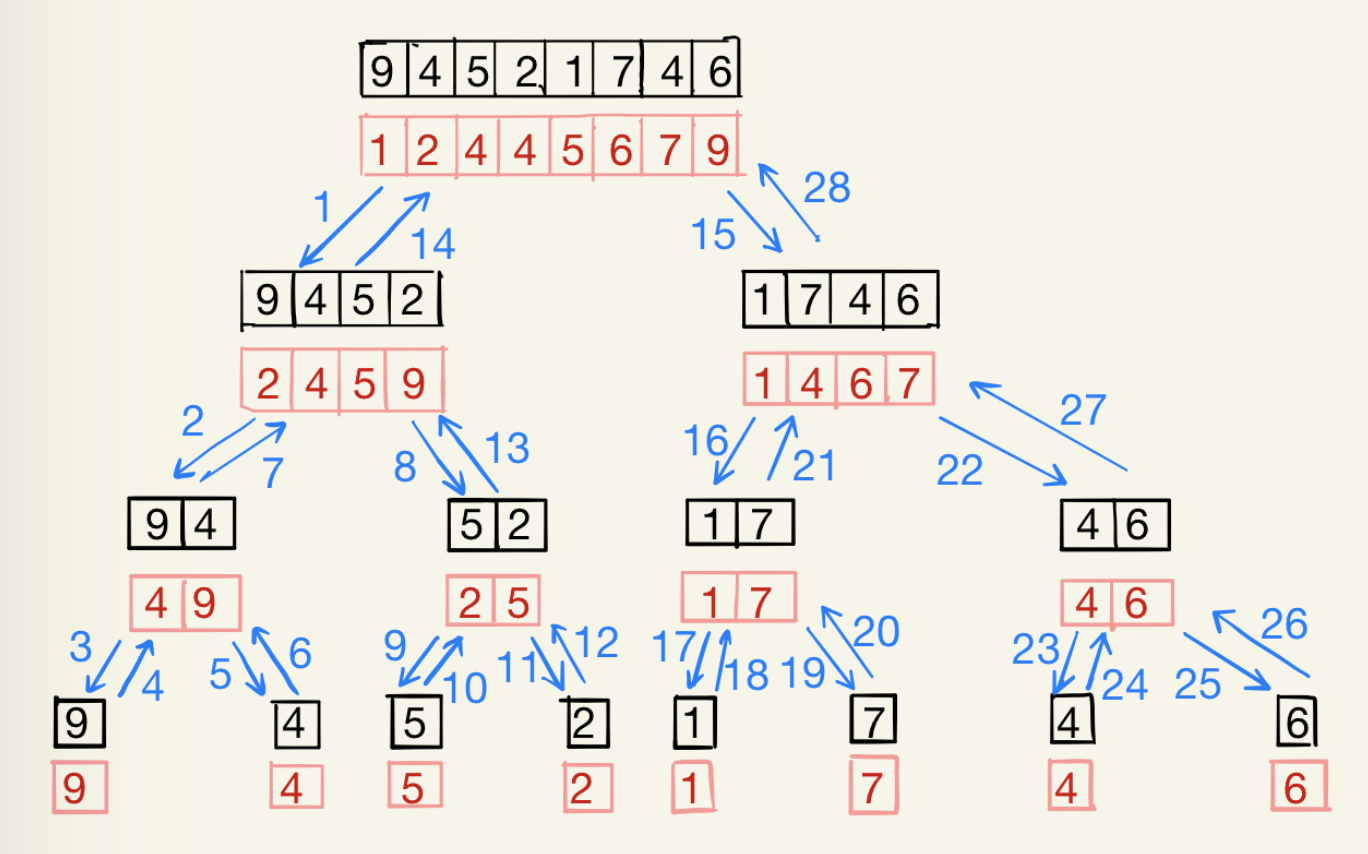
现在,给出归并排序的伪代码:
—————————-—— m e r g e _ s o r t merge_sort merge_sort——————————————
- 输入:待排序数组 A [ 1 … n ] A[1dots n] A[1…n]
- 输出:按非降序排列的数组 A [ 1 … n ] A[1dots n] A[1…n]
- 1. m e r g e _ s o r t ( A , 1 , n ) hspace{1cm}1.space merge_sort(A,1,n) 1. merge_sort(A,1,n)
- 过程: m e r g e _ s o r t ( A , l o w , h i g h ) merge_sort(A,low,high) merge_sort(A,low,high)
- 1. i f l o w < h i g h t h e n hspace{1cm}1.space ifspacespace low<highspacespace then 1. if low<high then
- 2. m i d ← ⌊ ( l o w + h i g h ) / 2 ⌋ hspace{1cm}2.spacehspace{1cm}midleftarrowlfloor(low+high)/2rfloor 2. mid←⌊(low+high)/2⌋
- 3. m e r g e _ s o r t ( A , l o w , m i d ) hspace{1cm}3.spacehspace{1cm}merge_sort(A,low,mid) 3. merge_sort(A,low,mid)
- 4. m e r g e _ s o r t ( A , m i d + 1 , h i g h ) hspace{1cm}4.spacehspace{1cm}merge_sort(A,mid+1,high) 4. merge_sort(A,mid+1,high)
- 5. m e r g e ( A , l o w , m i d , h i g h ) hspace{1cm}5.spacehspace{1cm}merge(A,low,mid,high) 5. merge(A,low,mid,high)
- 6. e n d i f hspace{1cm}6.space endspace if 6. end if
————————————————————————————————
复杂度分析
显然,上述算法中的基本运算是元素比较,换句话说,我们可以认为运行时间与由算法执行的元素比较次数是成正比的。因此现在的主要工作,就是计算出合并排序算法对数组
A
[
1
…
n
]
A[1dots n]
A[1…n] 排序时,总计执行的元素比较次数
C
(
n
)
C(n)
C(n)。首先,为了简便计算,我们不失一般性地假设
n
=
2
k
,
k
∈
N
n=2^k,kin N
n=2k,k∈N。
再回到伪代码,
当
n
=
1
n=1
n=1 时,算法不执行任何元素比较操作,即
C
(
1
)
=
0
C(1)=0
C(1)=0;
当
n
⩾
2
ngeqslant2
n⩾2 时,算法执行了步骤
2
∼
5
2sim5
2∼5,步骤
3
3
3 和
4
4
4 执行的元素比较操作都是
C
(
n
2
)
C(frac{n}{2})
C(2n) 次,根据合并操作算法的定义,易知合并两个子数组需要执行元素比较操作
2
n
∼
n
−
1
frac{2}{n}sim n-1
n2∼n−1 次。因此得到如下两个递推关系式:
-
最好情况: C ( n ) = { 0 i f n = 1 2 C ( n 2 ) + n 2 i f n ⩾ 2 C(n)=begin{cases}0hspace{1cm}ifspacespace n=1\\2C(frac{n}{2})+frac{n}{2}hspace{1cm}ifspacespace ngeqslant2end{cases} C(n)=⎩⎪⎨⎪⎧0if n=12C(2n)+2nif n⩾2,易得 C ( n ) = n log n 2 C(n)=frac{nlog n}{2} C(n)=2nlogn
-
最坏情况: C ( n ) = { 0 i f n = 1 2 C ( n 2 ) + n − 1 i f n ⩾ 2 C(n)=begin{cases}0hspace{1cm}ifspacespace n=1\\2C(frac{n}{2})+n-1hspace{1cm}ifspacespace ngeqslant2end{cases} C(n)=⎩⎪⎨⎪⎧0if n=12C(2n)+n−1if n⩾2,展开得
C ( n ) = 2 C ( n 2 ) + n − 1 C(n)=2C(frac{n}{2})+n-1 C(n)=2C(2n)+n−1
= 2 ( 2 C ( n 2 2 ) + n 2 − 1 ) + n − 1 hspace{0.85cm}=2(2C(frac{n}{2^2})+frac{n}{2}-1)+n-1 =2(2C(22n)+2n−1)+n−1
= 2 2 C ( n 2 2 ) + n − 2 + n − 1 hspace{0.85cm}=2^2C(frac{n}{2^2})+n-2+n-1 =22C(22n)+n−2+n−1
= ⋯ = 2 k C ( n 2 k ) + k n − 2 k − 1 − 2 k − 2 − ⋯ − 2 − 1 hspace{0.85cm}=cdots=2^kC(frac{n}{2^k})+kn-2^{k-1}-2^{k-2}-cdots-2-1 =⋯=2kC(2kn)+kn−2k−1−2k−2−⋯−2−1
= 2 k C ( 1 ) + k n − ∑ i = 0 k − 1 2 i hspace{0.85cm}=2^kC(1)+kn-sum_{i=0}^{k-1}2^i =2kC(1)+kn−∑i=0k−12i
= 0 + k n − ( 2 k − 1 ) hspace{0.85cm}=0+kn-(2^k-1) =0+kn−(2k−1)
= n log n − n + 1 hspace{0.85cm}=nlog n-n+1 =nlogn−n+1
综上,若
n
n
n 是任意正整数,则有合并排序算法执行的元素比较次数为
C
(
n
)
=
{
0
i
f
n
=
1
C
(
⌊
n
/
2
⌋
)
+
C
(
⌈
n
/
2
⌉
)
+
b
n
i
f
n
⩾
2
C(n)=begin{cases}0hspace{1cm}ifspacespace n=1\\ C(lfloor n/2rfloor)+C(lceil n/2rceil)+bnhspace{1cm}ifspacespace ngeqslant2end{cases}
C(n)=⎩⎪⎨⎪⎧0if n=1C(⌊n/2⌋)+C(⌈n/2⌉)+bnif n⩾2,其中
b
b
b 为非负常数,易知解为
C
(
n
)
=
Θ
(
n
log
n
)
C(n)=Theta(nlog n)
C(n)=Θ(nlogn),
进一步得到,算法的实际复杂度为
T
(
n
)
=
n
log
n
T(n)=nlog n
T(n)=nlogn。
实现
C C C++
void merge(int A[], int m, int p, int q, int r){
int B[m];
int s = p, t = q + 1, k = p;
while((s <= q) && (t <= r)){
if(A[s] <= A[t]) B[k] = A[s++];
else B[k] = A[t++];
k++;
}
if( s == q + 1){
for(int i=0; i<=r-k; i++) B[k+i] = A[t+i];
}else{
for(int i=0; i<=r-k; i++) B[k+i] = A[s+i];
}
for(int i=0; i<=r-p; i++) A[p+i] = B[p+i];
}
void merge_sort(int A[], int m, int low, int high){
if(low < high){
int mid = (low + high) / 2;
merge_sort(A, m, low, mid);
merge_sort(A, m, mid+1, high);
merge(A, m, low, mid, high);
}
}
P y t h o n Python Python
def merge(A, m, p, q, r):
B = [];
for i in range(0, m):
B.append(0)
s, t, k = p, q+1, p;
while (s <= q) and (t <= r):
if A[s] <= A[t]:
B[k] = A[s]
s += 1
else:
B[k] = A[t]
t += 1
k += 1
if s == q+1:
for i in range(0, r-k+1):
B[k+i] = A[t+i]
else:
for i in range(0, r-k+1):
B[k+i] = A[s+i]
for i in range(0, r-p+1):
A[p+i] = B[p+i]
def merge_sort(A, m, low, high):
if low < high:
mid = int((low + high) / 2)
merge_sort(A, m, low, mid)
merge_sort(A, m, mid+1, high)
merge(A, m, low, mid, high)
return A
J a v a Java Java
public static void merge(int[] A, int m, int p, int q, int r){
int[] B = new int[m];
int s = p, t = q + 1, k = p;
while((s <= q) && (t <= r)){
if(A[s] <= A[t]) B[k] = A[s++];
else B[k] = A[t++];
k++;
}
if( s == q + 1){
for(int i=0; i<=r-k; i++) B[k+i] = A[t+i];
}else{
for(int i=0; i<=r-k; i++) B[k+i] = A[s+i];
}
for(int i=0; i<=r-p; i++) A[p+i] = B[p+i];
}
public static void mergeSort(int[] A, int m, int low, int high){
if(low < high){
int mid = (low + high) / 2;
mergeSort(A, m, low, mid);
mergeSort(A, m, mid+1, high);
merge(A, m, low, mid, high);
}
}
| 表格分割线 |
|---|
6. 希尔排序
算法原理
希尔排序算法实际上是直接插入排序算法的升级版。它的主要思路就是把序列中的元素按照下标的一定增量进行分组,然后再对每个分组执行直接插入排序算法。随着增量逐渐减少,每个分组包含的元素值也随之增加,当增量减至
1
1
1 时,所有元素都被分到一组之中,算法终止。下面我们以数组为例来深入学习一下算法的设计思路:
设
A
[
1
…
n
]
A[1dots n]
A[1…n] 为一实数数组;
- 首先,我们选择一个小于 n n n 的整数 d 1 d_1 d1 作为第一个增量,结合数组元素的下标索引将所有元素完成分组,分组标准即所有距离为 d 1 d_1 d1 的倍数的元素放在同一组中(实际上就是将数组下标划分成公差为 d 1 d_1 d1,首项不同的等差数列);
- 其次,针对各组分别进行直接插入排序;
- 再次,取第二个增量 d 2 < d 1 d_2<d_1 d2<d1,重复以上的分组和排序操作;
- 最终,直至所取的增量 d t = 1 , d t < d t − 1 < ⋯ < d 2 < d 1 d_t=1,d_t<d_{t-1}<cdots<d_2<d_1 dt=1,dt<dt−1<⋯<d2<d1,即所有元素放在同一组中,执行直接插入排序算法,排序完成。
增量的选取一半先选择数组大小的一半,以后依次减半,直至增量为 1 1 1。下面我们再根据一个具体的例子来消化一下上述算法:
| 待排序数组 | A [ 1 … n ] = { 49 , 38 , 65 , 97 , 76 , 13 , 27 , 48 , 55 , 4 } A[1dots n]={49,space38,space65,space 97,space76,space13,space27,space48,space55,space4} A[1…n]={49, 38, 65, 97, 76, 13, 27, 48, 55, 4} |
|---|---|
| d 1 = 5 d_1=5 d1=5,一趟分组 | A [ 1 … n ] = { A[1dots n]={ A[1…n]={ 49 49 49 , 38 38 38 , 65 65 65 , 97 97 97, 76 76 76 , 13 13 13 , 27 27 27 , 48 48 48 , 55 55 55 , 4 4 4 } } } |
| 一趟排序 | A [ 1 … n ] = { A[1dots n]={ A[1…n]={ 13 13 13 , 27 27 27 , 48 48 48 , 55 55 55 , 4 4 4 , 49 49 49 , 38 38 38 , 65 65 65 , 97 97 97, 76 76 76 } } } |
| d 2 = 2 d_2=2 d2=2,二趟分组 | A [ 1 … n ] = { A[1dots n]={ A[1…n]={ 13 13 13 , 27 27 27 , 48 48 48 , 55 55 55 , 4 4 4 , 49 49 49 , 38 38 38 , 65 65 65 , 97 97 97 , 76 76 76 } } } |
| 二趟排序 | A [ 1 … n ] = { A[1dots n]={ A[1…n]={ 4 4 4 , 27 27 27 , 13 13 13 , 49 49 49 , 38 38 38 , 55 55 55 , 48 48 48 , 65 65 65 , 97 97 97 , 76 76 76 } } } |
| d 3 = 1 d_3=1 d3=1,三趟分组 | A [ 1 … n ] = { 4 , 27 , 13 , 49 , 38 , 55 , 48 , 65 , 97 , 76 } A[1dots n]={4,space27,space13,space 49,space38,space55,space48,space65,space97,space76} A[1…n]={4, 27, 13, 49, 38, 55, 48, 65, 97, 76} |
| 三趟排序,排序完毕 | A [ 1 … n ] = { 4 , 13 , 27 , 38 , 48 , 49 , 55 , 65 , 76 , 97 } A[1dots n]={4,space13,space27,space 38,space48,space49,space55,space65,space76,space97} A[1…n]={4, 13, 27, 38, 48, 49, 55, 65, 76, 97} |
伪代码如下:
—————————-——
s
h
e
l
l
_
s
o
r
t
shell_sort
shell_sort——————————————
- 输入:待排序数组 A [ 0 … n − 1 ] A[0dots n-1] A[0…n−1],数组长度 n n n
- 输出:按非降序排列的数组 A [ 0 … n − 1 ] A[0dots n-1] A[0…n−1]
- 1. f l a g ← ⌊ n / 2 ⌋ hspace{1cm}1.space flagleftarrowlfloor n/2rfloor 1. flag←⌊n/2⌋
- 2. w h i l e f l a g > 0 hspace{1cm}2.space whilespacespace flag>0 2. while flag>0
- 3. f o r i ← f l a g t o n − 1 hspace{1cm}3.spacehspace{1cm}forspacespace ileftarrow flagspacespace tospacespace n-1 3. for i←flag to n−1
- 4. t ← A [ i ] ; j ← i − f l a g hspace{1cm}4.spacehspace{2cm}tleftarrow A[i]space;space jleftarrow i-flag 4. t←A[i] ; j←i−flag
- 5. w h i l e ( j ⩾ 0 a n d t < A [ j ) hspace{1cm}5.spacehspace{2cm}whilespacespace(jgeqslant0spacespace andspacespace t< A[j) 5. while (j⩾0 and t<A[j)
- 6. A [ j + f l a g ] ← A [ j ] hspace{1cm}6.spacehspace{3cm}A[j+flag]leftarrow A[j] 6. A[j+flag]←A[j]
- 7. j ← j − f l a g hspace{1cm}7.spacehspace{3cm}jleftarrow j-flag 7. j←j−flag
- 8. e n d w h i l e hspace{1cm}8.spacehspace{2cm}endspace while 8. end while
- 9. A [ j + f l a g ] ← t hspace{1cm}9.spacehspace{2cm}A[j+flag]leftarrow t 9. A[j+flag]←t
- 10. e n d f o r hspace{0.85cm}10.spacehspace{1cm}endspace for 10. end for
- 11. f l a g ← ⌊ f l a g / 2 ⌋ hspace{0.85cm}11.spacehspace{1cm}flagleftarrowlfloor flag/2rfloor 11. flag←⌊flag/2⌋
- 12. e n d w h i l e hspace{0.85cm}12.space endspace while 12. end while
————————————————————————————————
复杂度分析
希尔排序算法不需要大量的辅助空间,和归并排序算法一样易于实现。事实上,希尔排序是基于插入排序的一种算法,主要是在直接插入排序算法的基础上增加了一个新的特性,进而提高了效率,因此结合之前插入排序算法时间复杂度的计算,我们很容易得到希尔排序算法的时间复杂度为
O
(
n
3
2
)
O(n^{frac{3}{2}})
O(n23)。
可见,希尔排序在中等大小规模的输入中表现良好,对于规模非常大的输入就不是最优选择了。此外,希尔排序在最坏情况下的执行效率和平均情况相差不大。因此,许多程序员在开始排序工作时,都会先试试希尔排序,如果表现不好,再更改为快速排序这样更高级的排序算法(一是因为它比较难写,二则是因为快速排序算法在最坏情况下效率极低)。
实现
C C C++
void shell_sort(int A[], int n){
int flag = n / 2;
while(flag > 0){
for(int i=flag; i<n; i++){
int t = A[i], j = i - flag;
while(j >= 0 && t < A[j]){
A[j+flag] = A[j];
j -= flag;
}
A[j+flag] = t;
}
flag /= 2;
}
}
P y t h o n Python Python
def shell_sort(A, n):
flag = n // 2
while flag > 0:
for i in range(flag, n):
t, j = A[i], i - flag
while j >= 0 and t < A[j]:
A[j+flag] = A[j]
j -= flag
A[j+flag]= t
flag = flag // 2
return A
J a v a Java Java
public static void shellSort(int[] A, int n){
int flag = n / 2;
while(flag > 0){
for(int i=flag; i<n; i++){
int t = A[i], j = i - flag;
while(j >= 0 && t < A[j]){
A[j+flag] = A[j];
j -= flag;
}
A[j+flag] = t;
}
flag /= 2;
}
}
最后
以上就是霸气长颈鹿最近收集整理的关于排序算法(6种基础排序算法)排序算法的全部内容,更多相关排序算法(6种基础排序算法)排序算法内容请搜索靠谱客的其他文章。








发表评论 取消回复