前端必备数据结构：快速排序，两种不同思路解答，必会

239 阅读 0 评论 158 点赞

我是靠谱客的博主直率短靴，这篇文章主要介绍前端必备数据结构：快速排序，两种不同思路解答，必会，现在分享给大家，希望可以做个参考。

对于快速排序，一般有两种思路，但是两种思路的耗时不一样，我将分开讲述；
其复杂度是：O(nlog^n)

所有代码是基于 leetCode 912. 排序数组 验证

第一种：以数组的第一个数为基数：

实现思路：

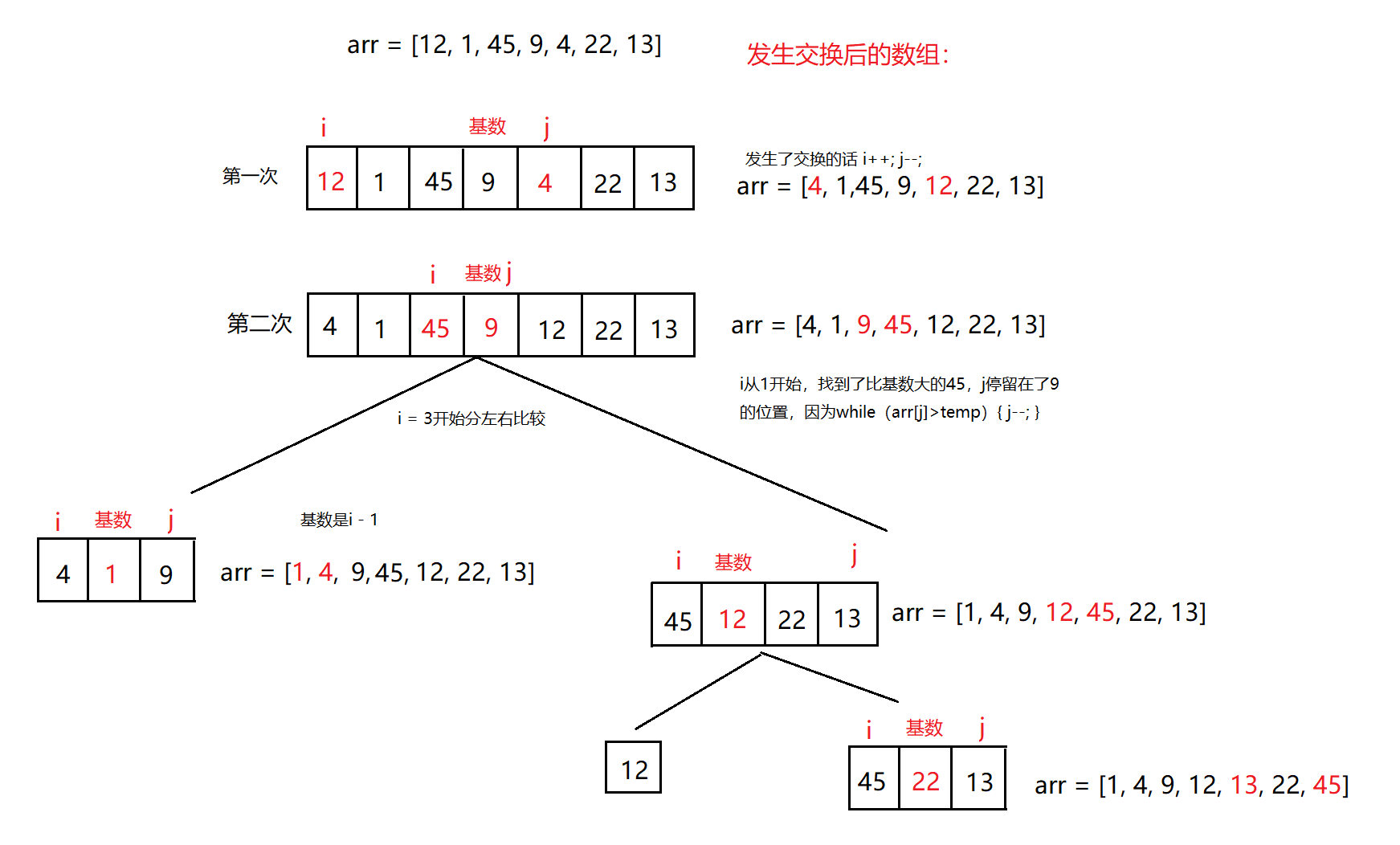
将数组的第一个数字作为基准，设置两个分别指向数组头部和尾部的指针 i 和 j ，首先向右移动 i，array[i] 小于基准值arr[0]，得到大于基准数的下标 i 停下左边的遍历。

同理：向左移动指针 j ，找到小于基准值的下标 j 。
此时进行两个值的交换。把小于基准值的放左边，大于基准值的放右边。

细节:

为了最后使得基准数字位于数组中间某个位置，它的左边的数字都比它小，它的右边的数字都比它大。
交换基准数与下标 i 上的值，然后递归对i左边以及右边的元素分别进行快速排序。

具体代码实现：

var sortArray = function(nums) {
    quickSort(0, nums.length - 1, nums)
    return nums;
};
var quickSort = function (left, right, arr){
    var temp = arr[left];
    var i = left;
    var j = right;
    if(i > j) return
    while(i < j) {
        while(arr[j] >= temp && j > i) {
            j--;
        }
        while(arr[i] <= temp && i < j) {
            i++;
        }
        
        [arr[i], arr[j]] = [arr[j], arr[i]]
    }
    //因为是以temp为界限，左边小于temp，右边大于temp，所以要把它放在最中间位置才合适。
    [arr[left], arr[i]] = [arr[i], arr[left]]
    
    quickSort(left, i-1, arr);
    quickSort(j+1, right, arr);
}

在这里插入图片描述

第二种：以数组的中间值为基数：

实现思路：

将数组的中间值作为基准，设置两个分别指向数组头部和尾部的指针 i 和 j ，首先向右移动 i，array[i] 小于基准值arr[0]，得到大于基准数的下标 i 停下左边的遍历。

同理：向左移动指针 j ，找到小于基准值的下标 j 。
此时进行两个值的交换。把小于基准值的放左边，大于基准值的放右边。然后递归基准值左边以及右边的元素分别进行快速排序。

以第一个数和中间值为基准值有什么区别？
对于一个几乎排好序的数组，采用第一个数为基准数是效率最差的表现。

在这里插入图片描述

具体代码实现：

var sortArray = function(nums) {
     quickSort(0, nums.length - 1, nums);
    return nums
};
var quickSort = function(left, right, arr) {
   if(left >= right) return
　　var temp = arr[Math.floor((left + right) / 2)]  
　　var i = left;
    var j = right;
    while(i <= j) {
        while(arr[i] < temp) {
            i++
        }
        while(arr[j] > temp) {
            j--
        }
         if(i <= j) {
         [arr[i], arr[j]] = [arr[j], arr[i]]
           i++;
            j--;
            
        }
     }
        quickSort(left, i-1, arr);
        quickSort(i, right, arr);
}