支持向量机(SVM)是作为一个经典并且高效的二分类模型,也有人认为这个是一个可以和神经网络抗衡的分类算法,即使在深度学习流行的现在也有它的一席之地,特别是在特征数量大于样本数量的高维特征空间场景下,具有速度快精度高的优点。而我在不断地死磕各路博客以及教学视频之后,终于对它有了简单的认识,下面就对SVM算法的原理进行记录。
算法目标
先上模具,假如有一堆训练数据集是线性可分的

构造一条直线将两个类数据进行分类,那么这种直线理论上有无数条,那么SVM的目标就是要找到其中最优的一条。从视觉上来看距离两类数据边界最远的那条直线貌似对数据的分类效果更好,所以SVM的目标就是找到一个超平面1,到数据边界的几何间隔最远,更专业的说明就是因为这条直线对数据样本局部扰动的容忍性更好。
在推导之前给定一系列的训练数据样本
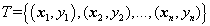
xi是第i个特征向量,yi是第i个样本标签,当yi等于+1时为正类,yi等于-1时未负类。再假设训练样本为线性可分的,并且决策平面为
0
=
w
T
x
+
b
0 = w^Tx + b
0=wTx+b,这样就有,当预测样本标签大于0时为正类,小于0时为负类
距离计算

存在一个超平面
0
=
w
T
x
+
b
0=w^Tx+b
0=wTx+b ,超平面法向量为w,其中一个训练样本 x ,平面内两个点x1,x2。利用向量点积计算样本点到超平面的距离,点到平面的几何间隔等于向量xx1与单位法向量的点积。
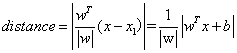
由于
w
T
x
1
=
−
b
w^Tx_1=-b
wTx1=−b,所以距离公式就换算成了与训练样本特征 x 相关的表达式。接下来再去绝对值,由于
y
i
y_i
yi 符号与
w
T
x
i
+
b
w^Tx_i+b
wTxi+b 符号相同,并且
y
i
y_i
yi要么是-1要么是1,所以等式右边乘以一个
y
i
y_i
yi就可以去掉绝对值。
最终样本点到超平面的几何间隔为:
d i t a n c e ( x , w , b ) = γ i = y i ∣ ∣ w ∣ ∣ ( w x i + b ) ditance(x,w,b) =γ_i=frac{y_i}{||w||}(wx_i+b) ditance(x,w,b)=γi=∣∣w∣∣yi(wxi+b)
其中
y
i
(
w
x
i
+
b
)
≥
0
y_i(wx_i+b)geq0
yi(wxi+b)≥0,现在我们让平面做一个缩放,一定能够找到一个值让
y
i
(
w
x
i
+
b
)
≥
1
y_i(wx_i+b)geq1
yi(wxi+b)≥1,既然做了这个缩放,那么这个就是一个约束条件,所以距离函数就变成了:
γ
i
=
y
i
∣
∣
w
∣
∣
(
w
x
i
+
b
)
gamma_i=frac{y_i}{||w||}(wx_i+b)
γi=∣∣w∣∣yi(wxi+b)
s.t. y i ( w x i + b ) ≥ 1 y_i(wx_i+b)geq1 yi(wxi+b)≥1
目标函数
SVM的策略是让超平面距离边界样本的距离最大,所以目标函数为:
a r g m a x w , b { 1 ∣ w ∣ m i n i [ y i ( w x i + b ) ] } underset {w,b}{arg max} {frac{1}{|w|}underset {i}{min}[y_i(wx_i+b)]} w,bargmax {∣w∣1imin[yi(wxi+b)]}
s.t. y i ( w x i + b ) ≥ 1 y_i(wx_i+b)geq1 yi(wxi+b)≥1
这样的话
y
i
(
w
x
i
+
b
)
y_i(wx_i+b)
yi(wxi+b)的最小值就是1,随即转换为在约束条件下,求解
1
∣
w
∣
frac{1}{|w|}
∣w∣1的最大值,实质上这个距离就是所谓的支持向量到超平面的距离,由前面推导的公式可得最终的超平面只跟支持向量有关,而支持向量就是数据样本的边界点。为了去掉绝对值,以及之后求导的方便,最终目标函数为:
m
i
n
w
,
b
1
2
w
2
underset {w,b}{min} frac{1}{2}w^2
w,bmin 21w2
s.t. y i ( w x i + b ) ≥ 1 y_i(wx_i+b)geq1 yi(wxi+b)≥1
函数求解
优化目标函数的方法用到了拉格朗日乘数法,这方法将一个 n 个变量与 k 个条件的最优化问题转换为 n+k 个变量的极值问题,其变量不受任何约束。由于个人能力不足,这个拉格朗日乘数法的原理,我也是没有弄清楚,只能直接利用别人的结论。
首先,将有约束的目标函数构造成无约束的拉格朗日目标函数:
L
(
w
,
b
,
α
)
=
1
2
w
2
−
∑
i
=
1
n
α
i
[
y
i
(
w
x
i
+
b
)
−
1
]
L(w,b,alpha)=frac{1}{2}w^2-displaystylesum_{i=1}^{n}alpha_i[y_i(wx_i+b)-1]
L(w,b,α)=21w2−i=1∑nαi[yi(wxi+b)−1]
其中拉格朗日乘子
α
i
≥
0
alpha_igeq0
αi≥0,这个是拉格朗日乘数法的约束条件。
再令:
θ ( w , b ) = m a x α i ≥ 0 L ( w , b , α ) theta(w,b)=underset{alpha_igeq0}{max} L(w,b,alpha) θ(w,b)=αi≥0max L(w,b,α)
当样本点不满足约束条件,
y
i
(
w
x
i
+
b
)
−
1
<
0
y_i(wx_i+b)-1<0
yi(wxi+b)−1<0时,将
α
i
alpha_i
αi取无穷大,则
θ
(
w
,
b
)
theta(w,b)
θ(w,b)也无穷大。
当样本点满足约束条件,
y
i
(
w
x
i
+
b
)
−
1
≥
0
y_i(wx_i+b)-1geq0
yi(wxi+b)−1≥0,
α
i
alpha_i
αi取0时,是目标函数本身
1
2
w
2
frac{1}{2}w^2
21w2。
合并起来后就得到了新的目标函数
θ
(
w
,
b
)
=
{
1
2
w
2
,
x
∈
可
行
区
域
+
∞
,
x
∈
不
可
行
区
域
theta(w,b)=begin{cases}frac{1}{2}w^2 & text{ , } xin可行区域 \ +infty & text{ , } xin不可行区域 end{cases}
θ(w,b)={21w2+∞ , x∈可行区域 , x∈不可行区域
对 θ ( w , b ) theta(w,b) θ(w,b)求最小值也是在求 1 2 w 2 frac{1}{2}w^2 21w2的最小值,于是原优化问题就等价于:
m i n θ ( w , b ) = m i n w , b m a x α ≥ 0 L ( w , b , α ) = p ∗ min theta(w,b)=underset{w,b}{min} underset{alphageq0}{max} L(w,b,alpha)=p* min θ(w,b)=w,bmin α≥0max L(w,b,α)=p∗
这样一个目标值函数,先求极大值再求极小值,这样的过程首先就要面对带有参数 w w w和 b b b参数的方程,而 α i alpha_i αi又是一个不等式约束,这样的求解过程不好做。所以这里还需要应用拉格朗日函数的对偶性,把最大值和最小值的位置调换一下:
m a x α ≥ 0 m i n w , b L ( w , b , α ) = d ∗ underset{alphageq0}{max} underset{w,b}{min} L(w,b,alpha)=d* α≥0max w,bmin L(w,b,α)=d∗
结论的证明过程倒是没有深究,这个结论我是直接参考支持向量机(SVM)——原理篇
要有
p
∗
=
d
∗
p*=d*
p∗=d∗,还要满足两个条件:
- 优化问题是一个凸优化问题
- 满足KKT条件
{ α i ≥ 0 y i ( w x i + b ) − 1 ≥ 0 α i [ y i ( w x i + b ) − 1 ] = 0 begin{cases}alpha_igeq0 & text{ } \ y_i(wx_i+b)-1geq0 & text{ } \ alpha_i[y_i(wx_i+b)-1]=0 & text{ } end{cases} ⎩⎪⎨⎪⎧αi≥0yi(wxi+b)−1≥0αi[yi(wxi+b)−1]=0
至此,目标函数:
m
a
x
α
i
≥
0
m
i
n
w
,
b
1
2
w
2
−
∑
i
=
1
n
α
i
[
y
i
(
w
x
i
+
b
)
−
1
]
underset{alpha_igeq0}{max} underset{w,b}{min} frac{1}{2}w^2-displaystylesum_{i=1}^{n}alpha_i[y_i(wx_i+b)-1]
αi≥0max w,bmin 21w2−i=1∑nαi[yi(wxi+b)−1]
约束条件为KKT条件
首先求最小值,对 w , b w,b w,b分别求偏导,令偏导等于0
{ w = ∑ i = 1 n α i y i x i ∑ i = 1 n α i y i = 0 begin{cases}w=displaystylesum_{i=1}^{n}alpha_iy_ix_i & text{ } \ displaystylesum_{i=1}^{n}alpha_iy_i=0 & text{ } end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧w=i=1∑nαiyixii=1∑nαiyi=0
把求解的值再往原函数代,这里我勤快一点,一步一步的写下来:
∑ i = 1 n α i y i x i ( 1 2 ∑ i = 1 n α i y i x i − ∑ i = 1 n α i y i x i ) − b ∑ i = 1 n α i y i + ∑ i = 1 n α i displaystylesum_{i=1}^{n}alpha_iy_ix_i(frac{1}{2}displaystylesum_{i=1}^{n}alpha_iy_ix_i-displaystylesum_{i=1}^{n}alpha_iy_ix_i)-bdisplaystylesum_{i=1}^{n}alpha_iy_i+displaystylesum_{i=1}^{n}alpha_i i=1∑nαiyixi(21i=1∑nαiyixi−i=1∑nαiyixi)−bi=1∑nαiyi+i=1∑nαi
= − 1 2 ∑ i = 1 n α i y i x i ∑ i = 1 n α i y i x i + ∑ i = 1 n α i =-frac{1}{2}displaystylesum_{i=1}^{n}alpha_iy_ix_idisplaystylesum_{i=1}^{n}alpha_iy_ix_i+displaystylesum_{i=1}^{n}alpha_i =−21i=1∑nαiyixii=1∑nαiyixi+i=1∑nαi
= − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i x j + ∑ i = 1 n α i =-frac{1}{2}displaystylesum_{i=1}^{n}displaystylesum_{j=1}^{n}alpha_ialpha_jy_iy_jx_ix_j+displaystylesum_{i=1}^{n}alpha_i =−21i=1∑nj=1∑nαiαjyiyjxixj+i=1∑nαi
求解最大值再换成求解最小值问题
m i n α i ≥ 0 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i x j − ∑ i = 1 n α i underset{alpha_igeq0}{min} frac{1}{2}displaystylesum_{i=1}^{n}displaystylesum_{j=1}^{n}alpha_ialpha_jy_iy_jx_ix_j-displaystylesum_{i=1}^{n}alpha_i αi≥0min 21i=1∑nj=1∑nαiαjyiyjxixj−i=1∑nαi
s . t . ∑ i = 1 n α i y i = 0 s.t. displaystylesum_{i=1}^{n}alpha_iy_i=0 s.t. i=1∑nαiyi=0
α i ≥ 0 , i = 1 , … , n alpha_igeq0,i=1,dots,n αi≥0,i=1,…,n
目标函数变成了特征向量之间的内积形式,一般的套路依然是对函数求偏导,再结合产生的约束条件,目标函数的极值是可求得。
根据这个算法求解得到α,在根据α求解得到w和b,就可以确定超平面
w
x
+
b
=
0
wx+b=0
wx+b=0
整理所有的约束条件
KKT:
{
α
i
≥
0
y
i
(
w
x
i
+
b
)
−
1
≥
0
α
i
[
y
i
(
w
x
i
+
b
)
−
1
]
=
0
begin{cases}alpha_igeq0 & text{ } \ y_i(wx_i+b)-1geq0 & text{ } \ alpha_i[y_i(wx_i+b)-1]=0 & text{ } end{cases}
⎩⎪⎨⎪⎧αi≥0yi(wxi+b)−1≥0αi[yi(wxi+b)−1]=0
w = ∑ i = 1 n α i y i x i w=displaystylesum_{i=1}^{n}alpha_iy_ix_i w=i=1∑nαiyixi
∑ i = 1 n α i y i = 0 displaystylesum_{i=1}^{n}alpha_iy_i=0 i=1∑nαiyi=0
由上可知,必定存在一个 α j > 0 color{red}alpha_j>0 αj>0(反证法,若全为0,则 w w w为0,矛盾)。对此有特征向量 j j j,存在 y j ( w x j + b ) − 1 = 0 y_j(wx_j+b)-1=0 yj(wxj+b)−1=0,由此就能求出 b 的值。
{ w = ∑ i = 1 n α i y i x i b = y j − ∑ i = 1 n α i y i x i x j , j 为 支 持 向 量 特 征 点 begin{cases}mathbf{w}=displaystylesum_{i=1}^{n}alpha_iy_ix_i & text{ } \ b= y_j-displaystylesum_{i=1}^{n}alpha_iy_ix_ix_j & text{ , } j为支持向量特征点 end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧w=i=1∑nαiyixib=yj−i=1∑nαiyixixj , j为支持向量特征点
对于所有的训练数据集样本,必定存在 α i = 0 alpha_i=0 αi=0或 y i ( w x i + b ) − 1 = 0 y_i(wx_i+b)-1=0 yi(wxi+b)−1=0,对于 α i = 0 alpha_i=0 αi=0样本点,这部分数据点不会对 w w w值有任何影响, w w w值只与 α i ≠ 0 alpha_ineq0 αi=0的支持向量有关,这部分从几何上看就是数据样本的边界,所以不管样本数据量怎么改动,最终的支持向量只要不变,超平面就不会随之改变。
求解完
w
w
w和
b
b
b之后,对于测试集特征向量
x
mathbf{x}
x,决策函数:
y
=
s
i
g
n
(
w
x
+
b
)
y=sign(mathbf{w}mathbf{x}+b)
y=sign(wx+b)
松弛变量
实际情况并不存在完全可以分离的两类数据集,特别是对于存在噪声点的数据,所以引入“软间隔”的概念,允许存在某些点不满足约束。引用一张图片作为例子,蓝色点存在一个噪声,把这个噪声点作为边界的话,到超平面的几何间隔就会小很多,允许这个点不满足约束条件,那么间隔就会更宽。

实际运用SVM算法会加入一个松弛变量,让约束条件不那么苛刻:
m
i
n
w
,
b
,
ξ
1
2
w
2
+
C
∑
i
=
1
n
ξ
i
underset{w,b,xi}{min} frac{1}{2}w^2+Cdisplaystylesum_{i=1}^{n}xi_i
w,b,ξmin 21w2+Ci=1∑nξi
s . t . y i ( w x i + b ) ≥ 1 − ξ i s.t. y_i(wx_i+b)geq1-xi_i s.t. yi(wxi+b)≥1−ξi
约束条件变得不那么严格,但是目标函数求最小值,限制了松弛变量也不能无穷无尽地变大。每一个变量都有一个
ξ
i
xi_i
ξi参数,表示不同数据样本不满足约束条件的程度。C>0参数是一个惩罚项参数,当C越大,约束条件越严格,允许不满足约束的点的数量就更少。
引入松弛变量之后,再用以上方法进行求解,新的拉格朗日函数:
m a x α i ≥ 0 m i n w , b , ξ 1 2 w 2 + C ∑ i = 1 n ξ i − ∑ i = 1 n α i [ y i ( w x i + b ) − 1 + ξ i ] − ∑ i = 1 n ω i ξ i underset{alpha_igeq0}{max} underset{w,b,xi}{min} frac{1}{2}w^2+Cdisplaystylesum_{i=1}^{n}xi_i-displaystylesum_{i=1}^{n}alpha_i[y_i(wx_i+b)-1+xi_i]-displaystylesum_{i=1}^{n}omega_ixi_i αi≥0max w,b,ξmin 21w2+Ci=1∑nξi−i=1∑nαi[yi(wxi+b)−1+ξi]−i=1∑nωiξi
分别对 w , b , ξ w,b,xi w,b,ξ求偏导,令偏导等于0:
{ w = ∑ i = 1 n α i x i y i ∑ i = 1 n α i y i = 0 C − α i − ω i = 0 , i = 1 , … , n begin{cases}w=displaystylesum_{i=1}^{n}alpha_ix_iy_i & text{ } \ displaystylesum_{i=1}^{n}alpha_iy_i=0 & text{ } \ C-alpha_i-omega_i=0 & text{ , } i= 1,dots,n end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧w=i=1∑nαixiyii=1∑nαiyi=0C−αi−ωi=0 , i=1,…,n
代入之后得到的表达式,跟之前没有加入松弛变量推导的表达式相同:
m i n α i ≥ 0 1 2 ∑ i = 1 n ∑ j = 1 n α i α j x i x j y i y j − ∑ i = 1 n α i underset{alpha_igeq0}{min} frac{1}{2}displaystylesum_{i=1}^{n}displaystylesum_{j=1}^{n}alpha_ialpha_jx_ix_jy_iy_j-displaystylesum_{i=1}^{n}alpha_i αi≥0min 21i=1∑nj=1∑nαiαjxixjyiyj−i=1∑nαi
与之前不同的地方在于,由于拉格朗日乘子 ω i ≥ 0 omega_igeq0 ωi≥0,所以 α i ≤ C alpha_ileq C αi≤C,给定不同的惩罚项参数C之后就会求解得出不同的超平面,具体的取值可以在实际情况中依据交叉验证进行选择。
核函数
前面所有的算法推导都是建立在决策边界是超平面的假设下进行的,当数据样本不是线性可分的时候,这个时候就需要将样本特征做一个映射处理,从低维空间映射到高维空间,这样就能用线性分类器对数据进行分类。
从低维到高维映射,映射之后还需要做向量的内积求解α,新增的这两个过程就给计算机带来了很大的运算量,所以核函数就此应运而生,让特征向量不需要做显式映射,就能够得到映射之后的向量内积。
核函数定义:假设函数φ是向量从一个低维特征空间到高维特征空间的映射,对于任意的低维特征向量x和z,都有
k ( x , z ) = ϕ ( x ) ⋅ ϕ ( z ) k(x,z)=phi(x)cdotphi(z) k(x,z)=ϕ(x)⋅ϕ(z)
称 k ( x , z ) k(x,z) k(x,z)为核函数。
引入核函数,既避免了高维特征空间中计算内积的恐怖计算量,又利用了样本在高维特征空间中线性可分的特性。核函数本质上是一个低维空间运算的结果,并没有采用从低维到高维的映射处理,但是等价于低维映射到高维之后再计算向量内积的值。
常用核函数:
- 线性核函数’ linear '。主要用于特征数量特别多,数据样本线性可分,速度快性能强。
- 高斯(RBF)核函数。应用比较广,能够实现低维向高维空间的处理。这个核函数应用比较广,无论大样本还是小样本都有很好的性能。
- sigmoid核函数。采用这个核函数,SVM就是一种多层神经网络。
大多情况面对的都是线性不可分的数据,需要的就是增加维度,降低样本数量跟特征数量之间的差距,达到线性可分。至于核函数的选择,我也直接在这里引用别人的结论(来自吴恩达的课堂)
1、如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
2、如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
3、如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况
超平面:二维空间是直线,三维空间是平面,三维以上空间就是超平面 ↩︎
最后
以上就是重要小熊猫最近收集整理的关于多帅一小伙,非要硬钢SVM的全部内容,更多相关多帅一小伙内容请搜索靠谱客的其他文章。








发表评论 取消回复