概述
采样是将一个信号（即时间或空间上的连续函数）转换成一个数值序列（即时间或空间上的离散函数）。采样过程所应遵循的规律，又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据。
奈奎斯特抽样定理：若f(t)是一个频带限制在（0，fh）内的时间连续信号，要想抽样后的信号能够不失真地还原出原信号，则必须抽样频率fs大于或等于信号最高频率分量fh的两倍，或说信号的最高频率不得大于折叠频率fs/2，即fs≥2fh。
f(t)也可能不是频带宽度有限的信号,因此为了避免频率响应的混叠，一般都在抽样器前加入一个保护性的前置低通预滤波器，称为防混叠滤波器，其截止频率为fs/2，以便滤除f(t)中高于fs/2的频率分量。
有时，也将满足抽样定理的抽样频率称为奈奎斯特抽样(速)率。将fs/2也称为奈奎斯特频率。
周期延拓：
欠采样：采样频率fs低于信号最高频率fh的两倍即fs<2fh，这种采样被称为欠采样。
用采样率fs去对频率为fa的信号欠采样会产生频谱混叠，混叠频率f=kfs±fa（k=0，1，2……）。
用采样率100MHz的信号去采70MHz的信号会得到一个30MHz的混叠频率。
用采样率100MHz的信号去采299MHz的信号会得到一个1MHz的混叠频率。
补充：
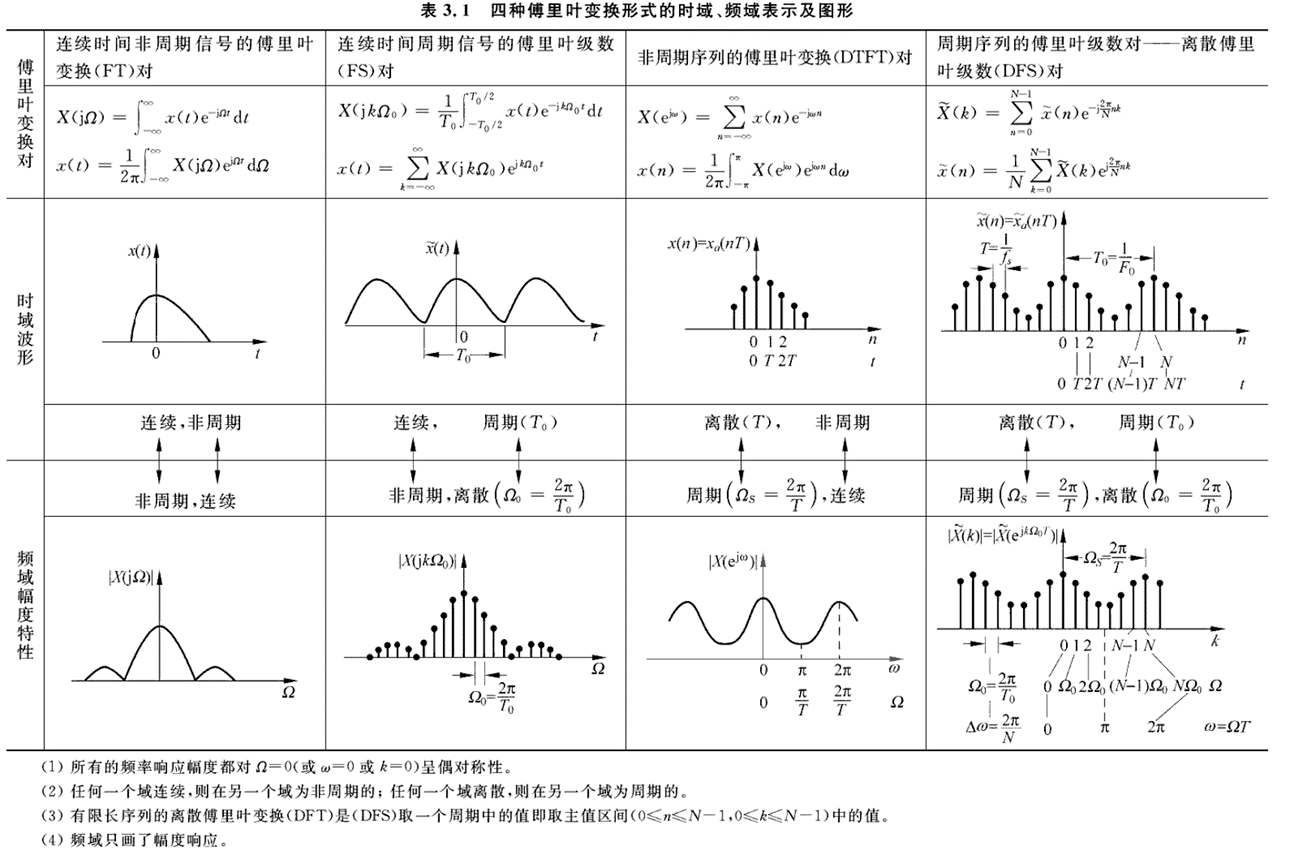
时域和频域之间的转换即傅里叶变换
最后
以上就是殷勤战斗机为你收集整理的抽样定理以及欠采样的全部内容，希望文章能够帮你解决抽样定理以及欠采样所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复