今天，从头捋一捋功率谱和能量谱

本文涉及关于功率谱和能量谱的几乎所有相关知识，虽然各个部分看起来有点分散，但都是干货。

1. 能量信号与功率信号

如果把 $f(t)$ 看做是电流关于的时间函数，单位为安培（A），那么 $f(t)$ 作用在 $1\Omega$ 的电阻上消耗的瞬时功率为 $|f(t){|}^2$ 。如果站在上帝的角度来看，自盘古开天辟地 ($t=-\infty$) 到宇宙完全毁灭 ($t=\infty$) 这个电阻消耗的总能量为：
$$E={\int }_{-\infty }^{\infty }|f(t){|}^2\mathrm{d}t$$
那么，这个电阻在宇宙的有生之年消耗的平均功率为：
$$P=\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}|f(t){|}^2\mathrm{d}t$$
上帝指示:

• 如果 $E$ 是一个非无穷大也非0的常数，那么 $f(t)$ 就定义为能量有限信号，简称能量信号。显然，能量信号的平均功率 $P$ 为0；
• 如果 $P$ 是一个非无穷大也非0的常数，比如 $f(t)$ 为周期信号或者统计量满足某一分布的随机信号时，那么 $f(t)$ 就定义为功率有限信号，简称功率信号。显然，功率信号的能量 $E$ 为无穷大。

显然，能量信号在无穷远处一定是收敛的；显然，功率信号肯定比能量信号有着更大的能量。

2. 相关函数

相关函数是鉴别信号的有力工具，被广泛应用于雷达回波的识别，通信同步信号的识别等领域。相关函数也称为相关积分，它与卷积的运算方法非常类似。

2.1 能量信号的相关函数

对于实函数 $f_1(t)$ 和 $f_2(t)$ ，如果他们是能量信号的话，他们之间的互相关函数定义如下：
$$R_{12}(\tau )={\int }_{-\infty }^{\infty }{f}_1(t)f_2(t-\tau )dt={\int }_{-\infty }^{\infty }{f}_1(t+\tau )f_2(t)dt$$
注意，下脚的标号在前面的信号领先 $\tau$ . 所以也可以说 $f_2(t)$ 和 $f_1(t)$ 的互相关函数定义为：
$$R_{21}(\tau )={\int }_{-\infty }^{\infty }{f}_1(t-\tau )f_2(t)dt={\int }_{-\infty }^{\infty }{f}_1(t)f_2(t+\tau )dt$$
一般情况下，$R_{12}(\tau )\ne R_{21}(\tau )$ ，因为下脚的标号在前面的信号领先 $\tau$ , 所以也可以理解为下脚的标号在后面的信号领先 $-\tau$ ，即：$R_{12}(\tau )=R_{21}(-\tau ),R_{21}(\tau )=R_{12}(-\tau )$

假如说 $f_1(t)$ 和 $f_2(t)$ 是同一信号，都记为 $f(t)$ ,这时就不需要对 $R_{12}(\tau )$ 和 $R_{21}(\tau )$ 进行区分，此时的相关函数称为自相关函数，即：
$$R(\tau )={\int }_{-\infty }^{\infty }f(t)f(t-\tau )dt={\int }_{-\infty }^{\infty }f(t+\tau )f(t)dt$$
容易看出，对自相关函数有：$R(\tau )=R(-\tau )$ ，可见，$f(t)$ 的自相关函数 $R(\tau )$ 是时移 $\tau$ 的偶函数。

2.2 功率信号的相关函数

对于实函数 $f_1(t)$ 和 $f_2(t)$ ，如果他们是功率信号的话，他们之间的互相关函数定义如下：
$$\{\begin{array}{l}{R}_{12}(\tau )={\lim }_{T\to \infty }\left[\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}_1(t)f_2(t-\tau )\mathrm{d}t\right]\\ R_{21}(\tau )={\lim }_{T\to \infty }\left[\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}_1(t-\tau )f_2(t)\mathrm{d}t\right]\end{array}$$

自相关函数：
$$R(\tau )=\underset{T\to \infty }{\lim }\left[\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(t)f(t-\tau )\mathrm{d}t\right]$$

3. 相关与卷积的关系

下面以能量信号为例，梳理一下卷积与相关的联系：

两个函数 $f_1(t)$ 和 $f_2(t)$ 的卷积定义式为:
$$f_1(t)\ast f_2(t)={\int }_{-\infty }^{\infty }{f}_1(\tau )f_2(t-\tau )d\tau$$
而他们的互相关函数定义为：
$$R_{12}(\tau )={\int }_{-\infty }^{\infty }{f}_1(t)f_2(t-\tau )dt$$
将他们的自变量统一下，则有：
$$\begin{array}{r}\{\begin{array}{lc}{f}_1(t)\ast f_2(t)& ={\int }_{-\infty }^{\infty }{f}_1(\tau )f_2(t-\tau )d\tau \\ R_{12}(t)& ={\int }_{-\infty }^{\infty }{f}_1(\tau )f_2(\tau -t)d\tau \end{array}\end{array}$$
所以他们之间的关系就显而易见了：
$$R_{12}(t)=f_1(t)\ast f_2(-t)$$
由上式可知，若 $f_1(t)$ 和 $f_2(t)$ 均为实偶函数，则卷积与相关的形式完全相同。

4. 帕塞瓦尔定理

由本文第一部分知 $f(t)$ 能量为：
$$E={\int }_{-\infty }^{\infty }|f(t){|}^2\mathrm{d}t$$
帕塞瓦尔定理指的是时域和频域内能量是守恒的，若 $f(t)$ 的傅里叶变换为 $F(j\omega )$ ，则该定理可以用公式表示为：
$$E={\int }_{-\infty }^{\infty }|f(t){|}^2\mathrm{d}t=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }|F(j\omega ){|}^2\mathrm{d}\omega$$
证明如下：

因为 $f(t)$ 的傅里叶变换 $F(j\omega )$ 为：
$$F(j\omega )={\int }_{-\infty }^{\infty }f(t){\mathrm{e}}^{-j\omega t}\mathrm{d}t$$
记 $F(j\omega )$ 的共轭为 $F^{\ast }(j\omega )$ ，假设 $f(t)$ 为复信号（这样假设适用性更广，也适用于实信号），则：
$$F^{\ast }(j\omega )={\int }_{-\infty }^{\infty }{f}^{\ast }(t){\mathrm{e}}^{j\omega t}\mathrm{d}t$$
所以
$$\begin{array}{rl}{\int }_{-\infty }^{\infty }|F(j\omega ){|}^2\mathrm{d}\omega & ={\int }_{-\infty }^{\infty }F(j\omega )F^{\ast }(j\omega )\mathrm{d}\omega \\ & ={\int }_{-\infty }^{\infty }F(j\omega ){\int }_{-\infty }^{\infty }{f}^{\ast }(t){\mathrm{e}}^{j\omega t}\mathrm{d}td\omega \\ & ={\int }_{-\infty }^{\infty }{f}^{\ast }(t){\int }_{-\infty }^{\infty }F(j\omega ){\mathrm{e}}^{j\omega t}\mathrm{d}\omega dt\\ & ={\int }_{-\infty }^{\infty }{f}^{\ast }(t)\cdot 2\pi f(t)\mathrm{d}t\\ & =2\pi {\int }_{-\infty }^{\infty }|f(t){|}^2\mathrm{d}t\end{array}$$
所以有：
$$E={\int }_{-\infty }^{\infty }|f(t){|}^2\mathrm{d}t=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }|F(j\omega ){|}^2\mathrm{d}\omega$$
证毕.

5. 能量谱

对于能量信号，为了表征能量在频域中的分布情况，可以借助密度函数的概念，类比概率密度函数，我们可以使用能量密度函数 $E(\omega )$, 将其定义为单位频率内的信号能量。能量密度函数简称为能量频谱或能量谱.

如何得到 $f(t)$ 的能量谱 $E(\omega )$ 的表达式呢？

因为单位频率内的信号能量为 $E(\omega )$ ，所以在频带 $\mathrm{d}f$ 内信号的能量是 $E(\omega )\mathrm{d}f$, 那么信号在整个频率区间 $(-\infty ,\infty )$ 内的总能量还可以这么求：
$$E={\int }_{-\infty }^{\infty }E(\omega )\mathrm{d}f=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }E(\omega )\mathrm{d}\omega$$
将上式与帕塞瓦尔定理进行对比，则可以得到能量谱表达式为：
$$E(\omega )=|F(j\omega ){|}^2$$

6. 能量信号的自相关函数与能量谱是一对傅里叶变换

因为能量信号的自相关函数为：
$$R_{12}(\tau )=f_1(\tau )\ast f_2(-\tau )$$
由 时域卷积对应频域相乘 可得到互相关函数的傅里叶变换为：
$$\begin{array}{rl}\mathrm{F}\left[R_{12}(\tau )\right]& =\mathrm{F}\left[f_1(\tau {)}^{\ast }{f}_2(-\tau )\right]\\ & =\mathrm{F}\left[f_1(\tau )\right]\mathrm{F}\left[f_2(-\tau )\right]\\ & =F_1(j\omega )F_2(-j\omega )\\ & =F_1(j\omega )F_2^{\ast }(j\omega )\end{array}$$
所以自相关函数的傅里叶变换为：
$$\mathrm{F}\left[R(\tau )\right]=F(j\omega )F^{\ast }(j\omega )=|F(j\omega ){|}^2=E(\omega )$$
所以说，能量信号的自相关函数与能量谱是一对傅里叶变换。

7. 功率谱

周期信号在时间上无始无终，能量必然是无限的，但功率可能是有限的；随机信号，能量也是无限的，且无法用确定的时间函数来表示，所以不存在频谱，这种情况下一般用功率谱来描述其频率特性。暂且把这当做为什么会存在功率谱的一种解释吧。

对于功率信号 $f(t)$ ，因为其能量是无穷大的，我们一般关注的是其平均功率 $P$，它的定义是：
$$P\stackrel{\mathrm{def}}{=}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}|f(t){|}^2\mathrm{d}t$$
如果 $f(t)$ 是实函数，则其平均功率定义为：
$$P\stackrel{\mathrm{def}}{=}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}^2(t)\mathrm{d}t$$
求功率谱的推导过程如下：

由于功率信号的能量是无穷的，且信号的持续时间是无限的，而计算功率又必须用到持续时间的信息带入上述公式，所以计算功率谱时会将信号进行截断然后取极限来完成，如下图，从 $ f(t)$ 中截取 $|t|\le T/2$ 的一段, 得到一个截尾函数 $f_T(t)$ ：

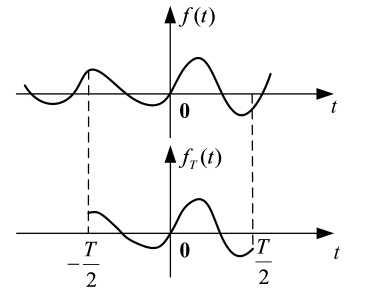
则 $f_T(t)$ 可以表示为:
$$f_T(t)=f(t)\left[\epsilon \left(t+\frac{T}{2}\right)-\epsilon \left(t-\frac{T}{2}\right)\right]$$
如果 $T$ 是有限值，则 $f_T(t)$ 的能量也是有限的。令:

$$F_T(j\omega )=\mathrm{F}\left[f_T(t)\right]$$
由帕斯瓦尔定理, $f_T(t)$ 的能量 $E_T$ 可表示为:
$$E_T={\int }_{-\infty }^{\infty }{f}_T^2(t)dt=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{\left|F_T(j\omega )\right|}^{2}d\omega$$

由于 ${\int }_{-\infty }^{\infty }{f}_T^2(t)dt={\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}^2(t)dt$ ，所以 $f(t)$ 的平均功率为：
$$\begin{array}{rl}P& \stackrel{\mathrm{def}}{=}\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}{f}^2(t)\mathrm{d}t\\ & =\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\infty }^{\infty }{f}_T^2(t)dt\\ & =\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\underset{T\to \infty }{\lim }\frac{1}{T}{\left|F_T(j\omega )\right|}^{2}d\omega \end{array}$$
类比能量密度函数的定义，定义 $P(\omega )$ 为功率密度函数，即单位频率内的信号功率，简称功率谱，那么信号在整个频率区间 $(-\infty ,\infty )$ 内的功率还可以这么求：
$$P={\int }_{-\infty }^{\infty }\mathrm{P}(\omega )\mathrm{d}f=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\mathrm{P}(\omega )\mathrm{d}\omega$$
比较得到：
$$\mathrm{P}(\omega )=\underset{T\to \infty }{\lim }\frac{{\left|F_T(j\omega )\right|}^2}{T}$$

8. 功率信号的自相关函数与功率谱是一对傅里叶变换

因为功率信号的自相关函数为(本文前面已经介绍)：
$$R(\tau )=\underset{T\to \infty }{\lim }\left[\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(t)f(t-\tau )\mathrm{d}t\right]$$
对两边同时取傅里叶变换，有：
$$\begin{array}{rl}\mathrm{F}[R(\tau )]& =\mathrm{F}\left[\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(t)f(t-\tau )\mathrm{d}t\right]\\ & =\mathrm{F}\left[\underset{T\to \infty }{\lim }\frac{1}{T}{\int }_{-\infty }^{\infty }{f}_T(t)f_T(t-\tau )\mathrm{d}t\right]\\ & =\mathrm{F}\left\{\underset{T\to \infty }{\lim }\frac{1}{T}\left[f_T(\tau {)}^{\ast }{f}_T(-\tau )\right]\right\}\\ & =\underset{T\to \infty }{\lim }\frac{1}{T}{\left|F_T(j\omega )\right|}^2\\ & =\mathrm{P}(\omega )\end{array}$$

所以说: 功率信号的自相关函数与功率谱是一对傅里叶变换.

本文首发于微信公众号振动信号研究所

最后

以上就是直率云朵为你收集整理的今天，从头捋一捋功率谱和能量谱的全部内容，希望文章能够帮你解决今天，从头捋一捋功率谱和能量谱所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。