使用Eigen进行位姿计算

1. 概述

在组合导航和slam等领域中，位姿计算是基础内容，使用Eigen来完成这一过程会大大减小工作量。姿态表示方法包括旋转向量、四元数、旋转矩阵、欧拉角，在使用Eigen之前，需要理清它们之间的关系。关于他们之间关系的基础介绍，网上已经有很多了，在此列出几篇博客，供参考：
https://blog.csdn.net/yang__jing/article/details/82316093
https://blog.csdn.net/u012706484/article/details/79147805
https://blog.csdn.net/qianniu_/article/details/79558199
鉴于此，本文章重点介绍的是我自己在使用过程中遇到的一些坑，供大家参考。

2. 使用方法

下面这张图描述了基本的转换关系，图片来自博客　https://blog.csdn.net/u011092188/article/details/77430988

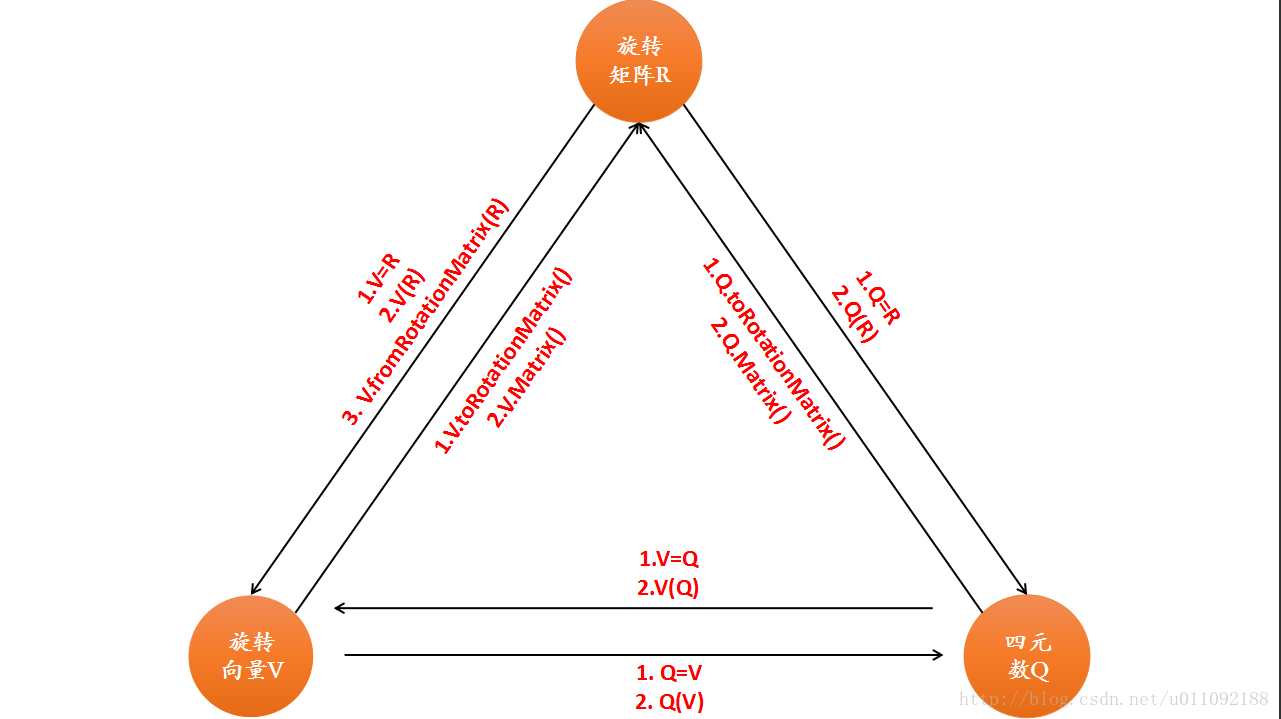
下面罗列了一些我自己使用过程中发现的一些注意事项：

• Eigen库里面重载的赋值运算符不能在声明的同时通过拷贝赋值。即Quaterniond Q1 = Q2是错误的。原因在于他的内部代码屏蔽了拷贝构造函数.。
• 欧拉角只与旋转矩阵有直接的转换关系，如果想转四元数或者旋转向量，只能通过旋转矩阵过渡一下。
• 所有的旋转都是逆时针为正，如果有做导航的朋友，往往北偏东为正，所以不要搞混。
• Eigen的旋转矩阵表示的是从旋转后的坐标系到旋转前坐标系的转换。即如果载体当前坐标系为A，初始参考坐标系为O，则Eigen的旋转矩阵R表示的是R_AO，即从A坐标系到O坐标系的转换关系，如果在A坐标系中有一个向量r_A，则它在O坐标系下的表示为r_O = R_AO * r_A。
• 和旋转矩阵一样，四元数和旋转向量表示的也是从旋转后的坐标系到旋转前坐标系的转换，因此在进行姿态更新的时候，所有的姿态增量都是右乘，例如当前旋转矩阵为R_AO，旋转到B坐标系以后，R_BO = R_AO * R_BA。四元数下的运算为Q_BO = Q_AO * Q_BA，旋转向量同理。
• 基于以上介绍的旋转顺序，从欧拉角到转转矩阵的运算就可以理解了。在机器人常见的坐标系定义中，绕X、Y、Z轴旋转的姿态角分别为roll、pitch、yaw，旋转顺序为Z->Y->X。则由欧拉角得到旋转矩阵的程序为：

Eigen::AngleAxis Vz(yaw, Eigen::Vector3f::UnitZ());
Eigen::AngleAxis Vy(pitch, Eigen::Vector3f::UnitY());
Eigen::AngleAxis Vx(roll, Eigen::Vector3f::UnitX());
Eigen::AngleAxis t_V;
t_V = Vz * Vy * Vx;
Eigen::Matrix3f t_R = t_V.matrix();

• 大家知道欧拉角是以旋转顺序为前提的，即如果旋转矩阵为R，则按照Z->Y->X和Z->X->Y的顺序得到的欧拉角是不同的(当然顺序不止这两种，一共有12种，不一一列举)，所以从旋转矩阵得到欧拉角时需要指定顺序，以机器人常用的Z->Y->X顺序为例，欧拉角为：

Eigen::Vector3f euler_angles = R.eulerAngles(2,1,0);

此处的2,1,0指的就是Z->Y->X，euler_angles里的三个值分别是yaw、pitch、roll，如果是2,0,1则顺序是Z->X->Y，则此时三个值是yaw、roll、pitch。需要注意的是，此处的顺序必须和上例中由欧拉角得到旋转矩阵时的旋转顺序相同，即旋转矩阵是按什么顺序产生的，则重新得到欧拉角时也应该按照相同的顺序得到，否则得到的值是错误的。

• 从Isometry3d中获取旋转矩阵是.rotation()函数，如果用.matrix()函数，得到的结果是整个四维矩阵，包含了平移量。同样的，可以用.translation()得到平移向量。
• Isometry3d的平移函数是.translate(Vector3d)，但它是在当前坐标系下平移（在导航中，即为载体坐标系）。
• Translation3d是表示平移的一种形式，构造函数为Translation3d(x,y,z),它可以直接和旋转向量、四元数、旋转矩阵相乘，得到的结果为Affine3d类型，在导航解算中，使用欧式变换更合适，因此可以用Afffine3d的matrix对Isometry3d的matrix赋值，也可以通过.rotation()和.translation()分别对旋转和平移赋值。
• 在对A坐标系下的一个点r_A（即一个三维向量）做投影，想得到它在O坐标系下的表示，即r_O时，它可以和任意形式的旋转表示形式相乘，包括四元数、旋转矩阵、旋转向量。即以下计算方法都是对的

r_O = Q_AO * r_A //利用四元数计算
r_O = R_AO * r_A //利用旋转矩阵计算
r_O = V_AO * r_A //利用旋转向量计算

• matrix.block(0,0,3,3)和matrix.block<3,3>(0,0)的区别是前者适用于变尺寸的区块，后者只能是固定尺寸，这一特性造成了他们用法上的一些区别：matrix.block<3,3>(0,0)可以当作一个matrix3f来用，可以和四元数、旋转向量进行赋值和构造时初始化，比如Q(M)和Q=M，但是matrix.block(0,0,3,3)不可以。两者都可以用作左值，即用别的矩阵对它赋值。需要注意的是两者都不能使用.eulerAngles这一类的函数，只有matrix3f可以。
• 向量的常用赋值方式是"<<"，不过这种赋值要维度相同，只对其中一部分赋值时，可用以下几个指令

x.head(n)   
x.head<n>()   
x.tail(n)       
x.tail<n>()    
x.segment(i, n) 
x.segment<n>(i) 

• 向量和矩阵之间可以互相赋值，向量是行向量，所以用矩阵的一部分给它赋值时候要注意形式一定是按行排列，如果按列，则要转置，可以转置矩阵，也可以转置向量。而用向量给矩阵赋值则不用在乎是否是行或列。例如matrix.block<3,1>(0,0)=vector是可以的。

下面贴出我做验证时所用的代码：

/*
 * @Description: 
 * @Author: Ren Qian
 * @LastEditors: Please set LastEditors
 * @Date: 2019-02-28 17:02:10
 * @LastEditTime: 2019-04-02 15:36:53
 */
#ifndef _TEST_ROTATION_HPP
#define _TEST_ROTATION_HPP

#include <iostream>
#include <string>
#include <Eigen/Dense>

using std::cout;
using std::endl;
using namespace Eigen;

static const double _init_angle = M_PI / 6;
static const double _euler_z = M_PI / 3;
static const double _euler_y = M_PI / 6;
static const double _euler_x = M_PI / 12;

AngleAxisd InitAngleAxis() {
    AngleAxisd t_V(_init_angle, Vector3d(0, 0, 1));
    return t_V;
}

Matrix3d InitMatrix() {
    // Matrix3d t_R(InitAngleAxis());//方法一
    Matrix3d t_R; t_R = InitAngleAxis();//方法二
    // Matrix3d t_R; t_R << cos(_init_angle),-sin(_init_angle),0.0,//方法三，这种方法得到的欧拉角会有问题
    //                     sin(_init_angle),cos(_init_angle),0.0,
    //                     0.0,0.0,1.0;
    return t_R;
}

Quaterniond InitQuaternion() {
    // double A = _init_angle;
    // Vector3d v(0, 0, 1);
    // Quaterniond t_Q(cos(A/2.0), v(0)*sin(A/2.0), v(1)*sin(A/2.0), v(2)*sin(A/2.0));//方法一，可能同样不适合反求欧拉角，还没验证
    Quaterniond t_Q(InitAngleAxis());
    return t_Q;
}

Isometry3d InitIsometry() {
    // Isometry3d t_T(InitAngleAxis());//方法一
    // Isometry3d t_T(InitMatrix());//方法二
    Isometry3d t_T(InitQuaternion());//方法三
    // Isometry3d t_T; t_T = InitAngleAxis();//方法四
    // Isometry3d t_T; t_T = InitMatrix();//方法五
    // Isometry3d t_T; t_T = InitQuaternion();//方法六
    t_T.pretranslate(Vector3d(0.0,0.0,0.0));
    return t_T;
}

Matrix3d angleAxis_to_matrix(AngleAxisd t_V) {
    // Matrix3d t_R(t_V);//方法一
    Matrix3d t_R; t_R = t_V;//方法二
    // Matrix3d t_R = t_V.toRotationMatrix();//方法三
    // Matrix3d t_R = t_V.matrix();//方法四
    return t_R;
    Isometry3d iso;
}

Matrix3d quaternion_to_matrixd(Quaterniond t_Q) {
    // Matrix3d t_R(t_Q);//方法一
    Matrix3d t_R; t_R = t_Q;//方法二
    // Matrix3d t_R = t_Q.toRotationMatrix();//方法三
    // Matrix3d t_R = t_Q.matrix();//方法四
    return t_R;
}

AngleAxisd matrix_to_angleAxis(Matrix3d t_R) {
    // AngleAxisd t_V(t_R);//方法一
    AngleAxisd t_V; t_V = t_R;//方法二，注意不能在声明的同时赋值
    return t_V;
}

AngleAxisd quaternion_to_angleAxis(Quaterniond t_Q) {
    // AngleAxisd t_V(t_Q);//方法一
    AngleAxisd t_V; t_V = t_Q;//方法二，注意不能在声明的同时赋值
    return t_V;
}

Quaterniond matrix_to_quaternion(Matrix3d t_R) {
    // Quaterniond t_Q(t_R);//方法一
    Quaterniond t_Q; t_Q = t_R;//方法二，注意不能在声明的同时赋值
    return t_Q;
}

Quaterniond angleAxis_to_quaternion(AngleAxisd t_V) {
    // Quaterniond t_Q(t_V);//方法一
    Quaterniond t_Q; t_Q = t_V;//方法二，注意不能在声明的同时赋值
    return t_Q;
}

Eigen::Matrix3d rotateX(double angle) {
    Eigen::Matrix3d t_R;
    t_R << 1,0,0,0,cos(angle),sin(angle),0,-sin(angle),cos(angle);
    return t_R;
}

Eigen::Matrix3d rotateY(double angle) {
    Eigen::Matrix3d t_R;
    t_R << cos(angle),0,-sin(angle),0,1,0,sin(angle),0,cos(angle);
    return t_R;
}

Eigen::Matrix3d rotateZ(double angle) {
    Eigen::Matrix3d t_R;
    t_R << cos(angle),sin(angle),0,-sin(angle),cos(angle),0,0,0,1;
    return t_R;
}

#endif

最后

以上就是受伤钢铁侠为你收集整理的使用Eigen进行位姿计算的全部内容，希望文章能够帮你解决使用Eigen进行位姿计算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。