【AtCoder】【AGC010D】DecrementingDescriptionSolutionCode

48 阅读 0 评论 32 点赞

我是靠谱客的博主冷艳紫菜，最近开发中收集的这篇文章主要介绍【AtCoder】【AGC010D】DecrementingDescriptionSolutionCode，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Description

给出一个长度为n的序列 a <script type="math/tex" id="MathJax-Element-1">a</script>，A、B两个人轮流操作：
1. 选择一个不为1的数，将其-1；
2. 把序列中的所有数/g，g为所有数的gcd；

操作不了的人输。

Solution

博弈题一堆结论…

输的人肯定是拿到111111的局面，
设sum为序列所有数的和，
要想赢，肯定要避免拿到sum=n的情况，

当n为偶数时：如果一直拿到sum为奇数的情况，那么必赢，

结论1：n为偶数且sum为奇数时，先手必胜，否则必输；

我们先来看一下sum在经历了一次操作后的奇偶变化：

(图片来源，侵删)
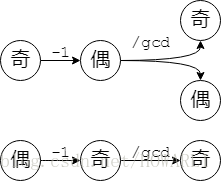
这里写图片描述

显然，先手可以让每一轮操作后都留给对手一个偶数，而对手只能还回来一个奇数，所以必赢；

偶数必输显然；

当n为奇数时：
结论2：n为奇数且sum为偶数时，先手必胜；
证明：先手要想赢，就必须不让对手还回来一个奇数，对手要想还回来一个奇数，就必须保证gcd不为0，
也就是说，对手在操作前，序列中所有数%gcd是这样的：0,0…,0,1
所以先手只要避免这种情况即可，那先手操作前的序列%gcd有这几种情况：
0,0,0,0,2
0,0,0,1,1
0,0,0,0,k+1
0,0,0,1,k
（后两个要除以那一局的gcd）

我们发现，这4种情况均可以破解，使之不变成0,0,0,0,1，

结论2：n为奇数且sum为奇数时，先手不一定输；
例：2,2,3，这样的话先手必赢，

先手肯定是必须给对手一个奇数，否则对手就赢了
所以就判断能否给对手一个奇数，显然每局如果可以的话方案唯一，
不行当前的人输
每次的gcd必须>1，所以是log次的。

Code

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fod(i,a,b) for(int i=a;i>=b;i--)
using namespace std;
typedef long long LL;
const int N=100500;
int read(int &n)
{
    char ch=' ';int q=0,w=1;
    for(;(ch!='-')&&((ch<'0')||(ch>'9'));ch=getchar());
    if(ch=='-')w=-1,ch=getchar();
    for(;ch>='0' && ch<='9';ch=getchar())q=q*10+ch-48;n=q*w;return n;
}
int m,n,ans;
int a[N];
int g[N];
int gcd(int x,int y){return y?gcd(y,x%y):x;}
int main()
{
    int w;
    LL q;
    read(n);
    fo(i,1,n)q+=(LL)read(a[i]);
    if(n==1&&a[1]==1)return printf("Secondn"),0;
    if(n==1)return printf("Firstn"),0;
    if(!(n&1))
    {
        if(q&1)printf("Firstn");
        else printf("Secondn");
        return 0;
    }
    if(!(q&1))return printf("Firstn"),0;
    for(bool I=0;1;I=!I)
    {
        g[n]=a[n];
        LL t=a[n]-1;
        fod(i,n-1,1)g[i]=gcd(g[i+1],a[i]),t+=(LL)a[i];
        bool OK=0;
        q=a[1];
        if(a[1]-1&&(1&(t/(ans=gcd(g[2],a[1]-1)))))OK=1,--a[1];
        else fo(i,2,n)if(a[i]-1)
        {
            w=gcd(q,a[i]-1);
            if(i<n)w=gcd(w,g[i+1]);
            if((1&(t/(ans=w))))
            {
                OK=1,--a[i];
                break;
            }
            q=gcd(q,a[i]);
        }else break;
        if(!OK)
        {
            if(I)printf("Firstn");
            else printf("Secondn");
            return 0;
        }
        fo(i,1,n)a[i]/=ans;
    }
    return 0;
}