AGC006 D

题意：
给出一个长度为2*n-1的排列，将除了头尾两个数变为相邻3个数的中位数，重复n-1次。
像这样

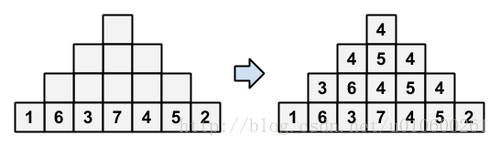
问最上面的数字是多少。
n<=100000

#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<iostream>
#define N 210000
using namespace std;
int n,m,a[N],b[N],ans,num;
struct node{int l,r,c;}A[N];
int solve(int lim)
{
    for(int i=1;i<=m;i++) b[i]=(a[i]>=lim);
    num=0;
    int i=1;
    while(i<m)
    {
        if(b[i]!=b[i+1]) {i++;continue;}
        A[++num].l=i;A[num].c=b[i];
        while(i<m && b[i+1]==b[i]) i++;
        A[num].r=i;
    }
    if(num==0) return b[1];
    A[0].r=0;
    for(int i=1;i<=num;i++)
    {
        int l=A[i-1].r+1,r=A[i].l-1;
        if(l>r) continue;
        int mid=(l+r)/2;
        A[i-1].r=mid;A[i].l=mid+1;
    }
    int l=A[num].r+1,r=m,mid;
    if(l<=r) {mid=(l+r)/2;A[num].r=mid;}
    for(int i=1;i<=num;i++) if(A[i].l<=n && A[i].r>=n) return A[i].c;
}
int main()
{
    scanf("%d",&n);
    m=2*n-1;
    for(int i=1;i<=m;i++) scanf("%d",&a[i]);
    int l=1,r=m;
    while(l<=r)
    {
        int mid=(l+r)/2;
        if(solve(mid)) ans=mid,l=mid+1;
        else r=mid-1;
    }
    printf("%dn",ans);
    return 0;
}

题解：
考虑想鏼爷的bc那题一样，二分一个数，把大于等于他的位置写1，小于的写-1，这样取中位数就变成了模2意义下的加法，统计出底层每个点到最上层的路径数算一下结果是1还是-1就好。然而算路径数我只想到了倍增fft，也许比赛时可以打个表>_<
其实我觉得我的模型很棒棒啊
膜了题解的做法，先二分，然后看一张01序列合并的图

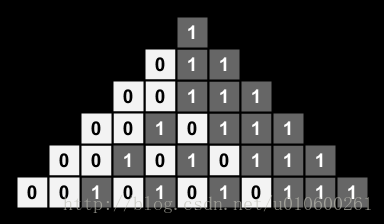
发现对于连续的0或1，他会一直向上伸。对于01交替，就会不停变小，直到两边的连续序列相交，处理一下每一段最后覆盖的区间就好。特判全部01交替的情况。

最后

以上就是真实蜗牛为你收集整理的AGC006 D的全部内容，希望文章能够帮你解决AGC006 D所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。