1. REPVGG

提出重参数化，训练和推理结构解耦。在ImageNet上，RepVGG达到80%以上的top-1精度，在NVIDIA 1080Ti GPU上，RepVGG模型运行速度比ResNet-50快83%，比ResNet-101快101%，具有更高的精度，并与最先进的模型如EfficientNet和RegNet相比显示了良好的精度-速度权衡。

在本文中，作者提出了一种超越许多复杂模型的vgg风格的RepVGG架构。RepVGG具有以下优点:

• 该模型具有类似vgg的平面(也称为前馈)结构，没有任何分支，这意味着每一层都将其唯一的前一层的输出作为输入，并将输出输入到唯一的后一层。
• 模型的主体仅使用$3\times 3$ 卷积和ReLU。
• 具体的架构(包括特定的深度和层宽)实例化不需要自动搜索，手动细化，复合缩放，也不需要其他繁重的设计。

多分支体系结构的优点都是用于训练的，而对推理来说是不可取的缺点，通过结构重新参数化来解耦训练时的多分支和推理时的纯平面结构，这意味着通过参数转换将一个体系结构转换为另一个体系结构。

文章贡献：

• 提出了RepVGG，这是一种简单的架构，与最先进的技术相比，具有良好的速度-精度权衡。
• 建议使用结构重参数化来解耦训练时的多分支结构和推理时的简单架构。
• 展示了RepVGG在图像分类和语义分割方面的有效性，以及实现的效率和易用性。

简言之，多分支对训练有利，通过重参数化将多分支转换为简单的平面模型，保证性能的前提下加速推理。

1.1 背景

经典的卷积神经网络VGG不仅在图像识别方面取得了巨大的成功，而且其架构简单，仅由堆叠的$3\times 3$卷积、ReLU和池化组成。随着 Inception ，ResNet， DenseNet的出现，越来越多的研究转移到良好设计的结构上，使得模型变得越来越复杂。也有一些研究是基于自动或手动的结构搜索，或者复合缩放策略等。

复合缩放策略：即从三个维度（depth，width，resolution）对模型进行缩放，通过神经网络架构搜索（NAS）的方式同时对这三个维度进行平衡，搜索得到最优网络架构。

复杂的多分支设计(如ResNet中的残差相加和Inception中的分支连接)使得模型难以实现和定制，降低了推理和内存利用率。

一些组件(如Xception和MobileNets中的深度可分离卷积和ShuffleNets中的channel shuffle)增加了内存访问成本，并且在各种设备上缺乏支持，除了这些因素以外还有许多因素影响了推理速度。

文中提到FLOPs并不能精确反映真实推理速度。FLOPs低的不一定意味着推理速度快。还有两个重要的因素对推理速度有相当大的影响，但没有被FLOPs考虑:内存访问成本(MAC)和并行度。例如，虽然分支相加或拼接的计算量可以忽略不记，但是MAC是重要的。在分组卷积中MAC也占据了大量的时间。另一方面，在相同的FLOPs下，具有高并行度的模型可能比另一个具有低并行度的模型快得多。总之，具有相同 FLOPs的操作可能具有不同的运行时间，具体取决于平台。

1.2 重参数化

重参数化具体来说，就是使用恒等映射(identity)和1×1分支构造了训练时的RepVGG（即在原来$3\times 3$卷积的基础上增强$1\times 1$、恒等映射两个分支），这是受ResNet的启发，但采用了不同的方式，可以通过结构重参数化来删除分支。经过训练后，用简单代数进行变换，将一个恒等映射分支看作是一个退化的1×1 卷积，1×1分支可以进一步看作是一个退化的3 × 3卷积，这样我们就可以用原始3 × 3卷积核、恒等映射和1×1分支以及批归一化(BN)层的训练参数构造一个3 × 3卷积核。因此，转换后的模型由3 × 3卷积层堆叠而成，保存下来后用于测试和部署。

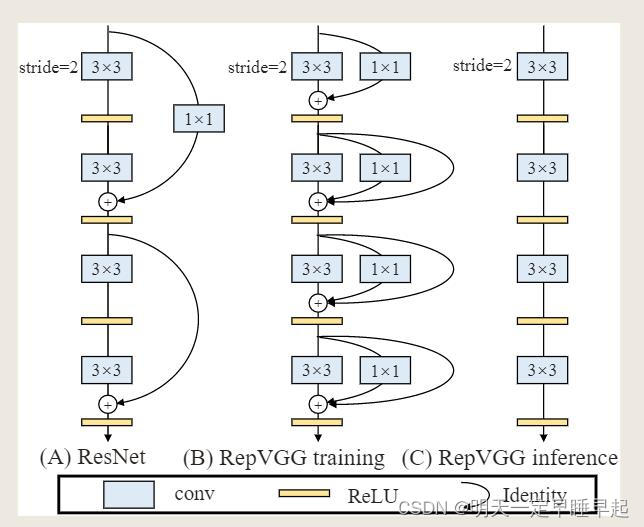
上图就是重参数化的大致过程，论文原文提到，值得注意的是，推理时RepVGG的主体只有一种类型的操作符:3 × 3 卷积，然后是ReLU，这使得RepVGG在gpu等通用计算设备上很快速。更好的是，RepVGG允许专门的硬件（指的应该是对3 × 3 卷积有优化）实现更高的速度，因为考虑到芯片的大小和功耗，我们需要的操作类型越少，我们可以集成到芯片上的计算单元就越多。因此，一个专门用于RepVGG的推理芯片可以有大量3×3-ReLU单元和更少的内存单元(因为纯平面结构是节省内存的)。

1.2.1 内存开销

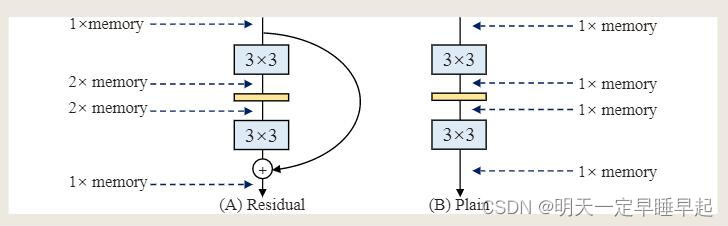
对比残差结构和平面结构，假设输入输出feature map的size相等，对于残差结构来说，输入要一直保持到相加为止，也就是说从进入分支结构开始后，内存的开销变为原来的两倍，直到相加后变回和输入一样的开销。而平面结构自始至终都是和输入一样的开销。

这里开销我个人理解成，输入在经过处理并将结果保存后就立即释放掉。在假设输入输出特征图大小一致的情况下，那么内存占用可以认为是没有变化的。也就是说每多一个分支就是多一份开销。

1.2.2 方法

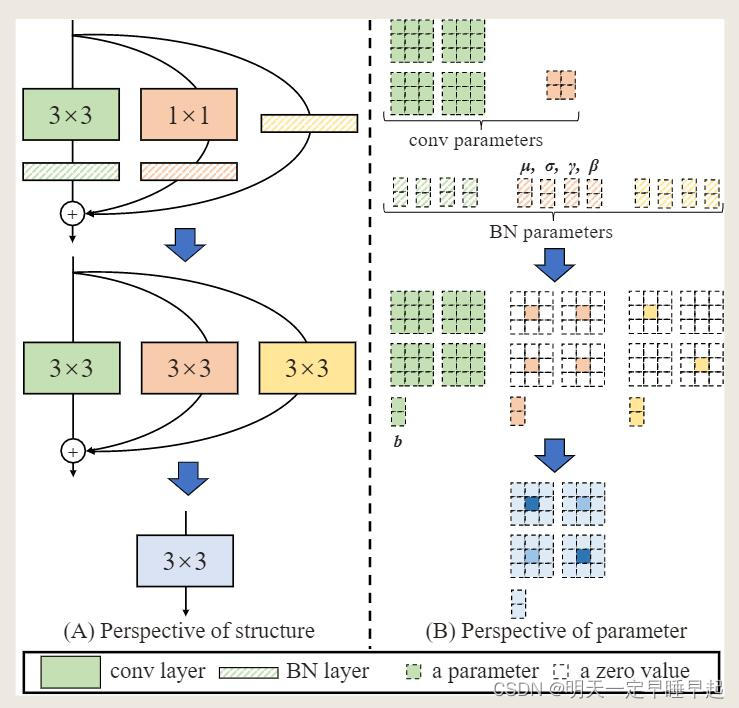
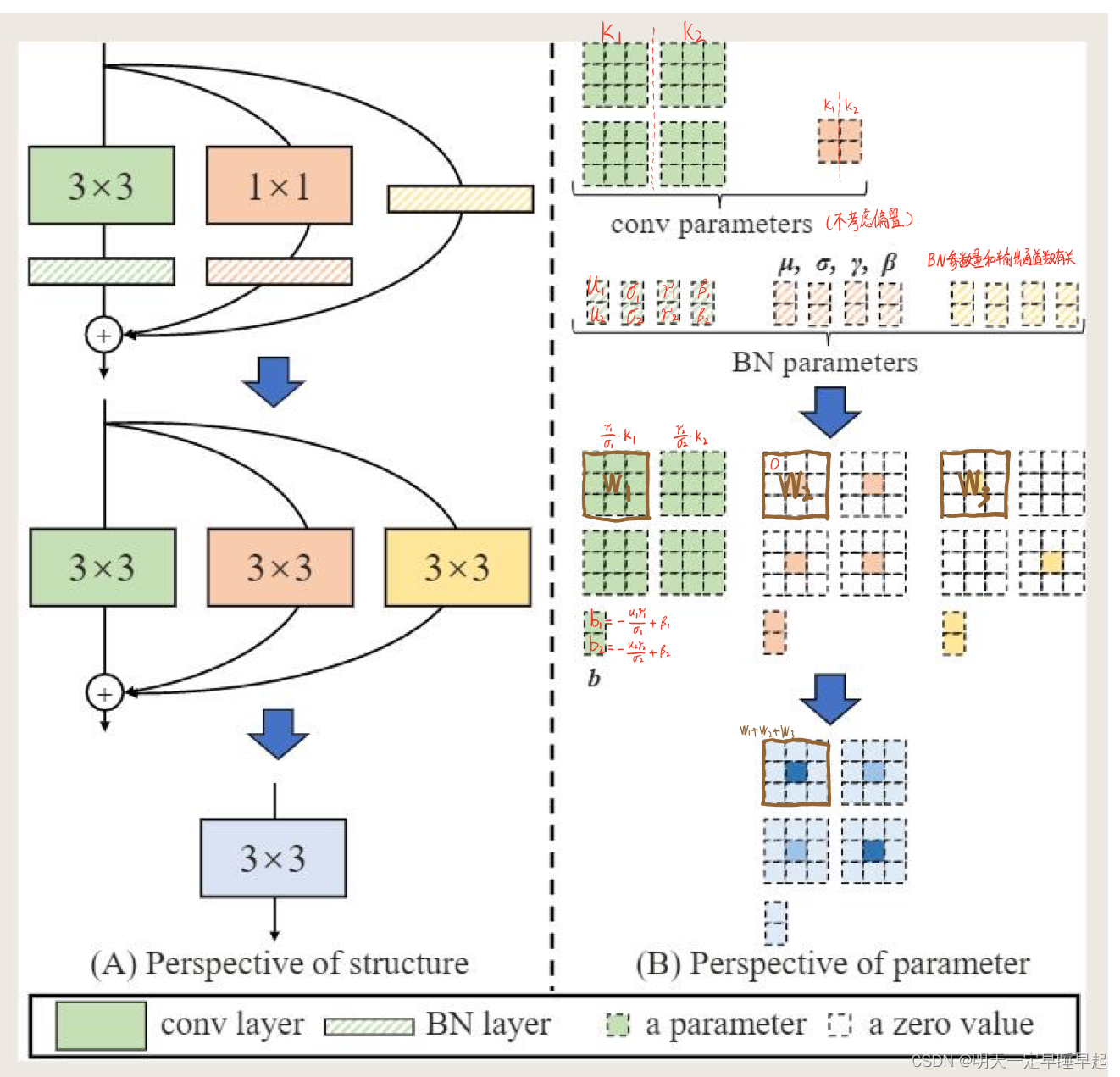
上图假设输入输出通道都是2。需要注意的是每层的每个分支相加之前都用了BN。设：
$W^{(3)}\in R^{C_2\times C_1\times 3\times 3}$为输入通道数$C_1$，输出通道数$C_2$的$3\times 3$卷积；
$W^{(1)}\in R^{C_2\times C_1}$为输入通道数$C_1$，输出通道数$C_2$的$1\times 1$卷积；
${\mu }^{(3)}，{\sigma }^{(3)}，{\gamma }^{(3)}，{\beta }^{(3)}$表示$3\times 3$卷积后的BN层；
${\mu }^{(1)}，{\sigma }^{(1)}，{\gamma }^{(1)}，{\beta }^{(1)}$表示$1\times 1$卷积后的BN层；
${\mu }^{(0)}，{\sigma }^{(0)}，{\gamma }^{(0)}，{\beta }^{(0)}$表示恒等映射后的BN层；
输入$M^{(}1)=\in R^{N\times C_1\times H_1\times W_1}$；
输出$M^{(}2)=\in R^{N\times C_2\times H_2\times W_2}$；
用$\ast$表示卷积操作。若$C_1=C_2,H_1=H_2$，则：
$$\begin{array}{rl}{M}^{(2)}& =bn(M^{(1)}\ast W^{(3)}，{\mu }^{(3)}，{\sigma }^{(3)}，{\gamma }^{(3)}，{\beta }^{(3)})\\ & +bn(M^{(1)}\ast W^{(1)}，{\mu }^{(1)}，{\sigma }^{(1)}，{\gamma }^{(1)}，{\beta }^{(1)})\\ & +bn(M^{(1)}，{\mu }^{(0)}，{\sigma }^{(0)}，{\gamma }^{(0)}，{\beta }^{(0)})\end{array}$$

若$C_1=C_2,H_1=H_2$的条件无法满足，那么恒等映射分支将不再适用，因此相当于只采取公式的前两个部分。注意这里的BN表示推理时的BN。

注意，BN在训练和推理时的计算方式不一样，具体可以参考BatchNorm怎样解决训练和推理时batch size 不同的问题？，回顾下BN的公式
$$y=\frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}\cdot \gamma +\beta$$

设$\forall 1\le i\le C_2$，则
$$bn(M,\mu ,\sigma ,\gamma ,\beta {)}_{:,i,:,:}=(M_{:,i,:,:}-{\mu }_i)\frac{{\gamma }_i}{{\sigma }_i}+{\beta }_i$$
首先把每个BN及其前一个卷积层转换为一个带偏置的卷积层。设 { W , μ , σ , γ , β } {W,mu,sigma,gamma,beta} {W,μ,σ,γ,β}最终转换核以及偏置为 { W ′ , b ′ } {W',b'} {W′,b′}的卷积。则
$$W_{i,:,:,:}^{\prime }=\frac{{\gamma }_i}{{\sigma }_i}{W}_{i,:,:,:},b_i^{\prime }=-\frac{{\mu }_i{\gamma }_i}{{\sigma }_i}+{\beta }_i$$
仍然有$\forall 1\le i\le C_2$

注意$i$表示的都是输出通道数$C_2$

$$bn(M\ast W,\mu ,\sigma ,\gamma ,\beta {)}_{:,i,:,:}=(M\ast W^{\prime }{)}_{:,i,:,:}+{\beta }_i^{\prime }$$

这种映射也适用于恒等映射分支，因为恒等映射分支可以被视为$1\times 1$卷积，单位矩阵为其核。经过变换后，我们得到了一个$3\times 3$核，两个$1\times 1$核，以及三个偏置向量。通过将三个偏置向量相加得到最终偏置。，将两个$1\times 1$核进行零填充成$3\times 3$核，相当于在$3\times 3$核上中心点添加$1\times 1$核得到$3\times 3$核，最终将3个$3\times 3$核相加。

可以参考博客RepVGG网络简介了解计算、代码细节。

最后附上自己的理解：

偏置相加没有画出来，但是和卷积参数相加是一样的原理。

最后感谢作者丁霄汉等人做出的贡献：结构重参数化：利用参数转换解耦训练和推理结构
​

最后

以上就是稳重乌龟为你收集整理的RepVGG论文阅读笔记1. REPVGG的全部内容，希望文章能够帮你解决RepVGG论文阅读笔记1. REPVGG所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。