机器学习实战笔记(1)
一、k-近邻算法
1、算法主要实现步骤
- 计算已知类别数据集中的点与当前点之间的距离(欧式距离公式);
- 按照距离递增次序排序;
- 选取与当前点距离最小的K个点;
- 确定前K个点所在类别出现频率;
- 返回前K个点出现频率最高的类别作为当前的点的预测分类;
2、示例1 约会配对
(1)数据散点图
对数据1、2列属性值绘制散点图如下(三种分类采用颜色区分)
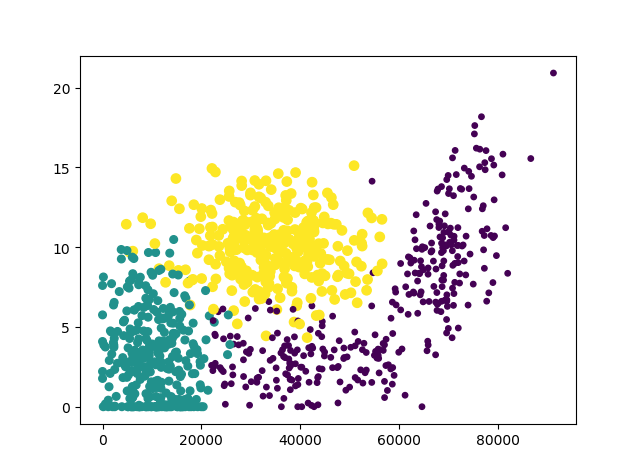
(2)判断所属分类
def classify0(inX, dataSet, labels, k):
'''计算该点到每个点的距离,选取前k个最小距离点,将k个点中标签计数,选取最多次数的标签作为该点预测'''
dataSetSize = dataSet.shape[0] # 返回数据行数
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet # 用inX"铺“出矩阵,采用矩阵计算避免采用循环
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1) # 行元素相加求和
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort() # 由小到大对distances数组排序
classCount = {}
for i in range(k): # 循环取前k个点
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1 # 计算各类lables个数
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) #按key(次数)从大到小排序
return sortedClassCount[0][0]
-
.shape() 返回维度,如3行*2列的矩阵则返回[3,2]
-
.tile()
-
.sum() 没有axis参数表示全部相加,axis=0表示按列相加,axis=1表示按照行的方向相加
(3)将文本记录转为矩阵数据
def file2matrix(filename):
love_dictionary = {'largeDoses':3, 'smallDoses':2, 'didntLike':1}
fr = open(filename)
arrayOLines = fr.readlines() # 按行读取数据作为数组存储
numberOfLines = len(arrayOLines) #(数组长度)get the number of lines in the file
returnMat = np.zeros((numberOfLines, 3)) # prepare matrix to return(按数据维度、数量改造全0元素数组)
classLabelVector = [] # prepare labels return
index = 0
for line in arrayOLines:
line = line.strip() # strip() 方法用于移除字符串头尾指定的字符(默认为空格)或字符序列
listFromLine = line.split('t') # 按‘t’分开
returnMat[index, :] = listFromLine[0:3] # 赋值到返回矩阵的具体行
if(listFromLine[-1].isdigit()): # 判断最后一列是否为纯数字
classLabelVector.append(int(listFromLine[-1])) # 为纯数字则直接将添加分类标签
else:
classLabelVector.append(love_dictionary.get(listFromLine[-1])) # 不是纯数字则添加字典中对应的类别数字
index += 1
return returnMat, classLabelVector
- numpy.zeros((x,y)) 初始化全0矩阵,其他数字同理
(4)归一化特征值
def autoNorm(dataSet):
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = np.zeros(np.shape(dataSet)) # 构造矩阵整体运算
m = dataSet.shape[0]
normDataSet = dataSet - np.tile(minVals, (m, 1)) # newValue = (oldValue-min)/(max-min)
normDataSet = normDataSet/np.tile(ranges, (m, 1)) #element wise divide
return normDataSet, ranges, minVals
- .min(0)返回该矩阵中每一列的最小值 .min(1)返回该矩阵中每一行的最小值
(5)最终测试
def datingClassTest():
hoRatio = 0.10 #hold out 10%(留前10%测试,其余作为已知点)
datingDataMat, datingLabels = file2matrix('t1/datingTestSet2.txt') #load data
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0] # m:总个数
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
if (classifierResult != datingLabels[i]): errorCount += 1.0
print("the total error rate is: %f" % (errorCount / float(numTestVecs)))
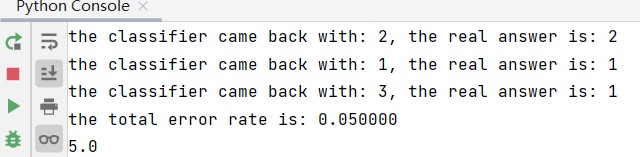
测试结果输出如下图所示:
二、线性回归(基于Normal Equation)
1、梯度下降 vs. 正规方程
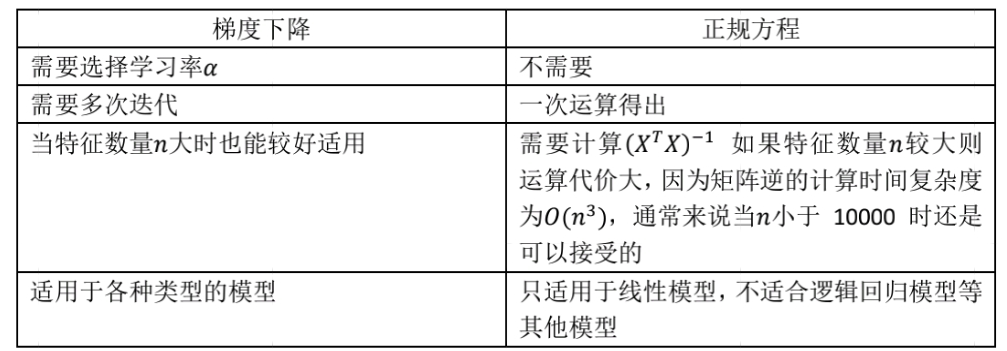
3、示例1(OLS,普通最小二乘法)
(1)计算公式
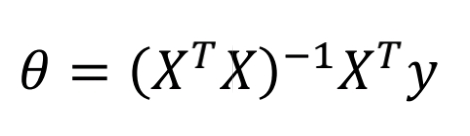
(2)读取数据文件
文件中数据格式:1.000000 0.067732 3.176513
def loadDataSet(fileName):
'''读取文件中除去目标值的数据(X0,X1)'''
numFeat = len(open(fileName).readline().split('t')) - 1 # (X0,X1,Y)除去结果Y,其中X0为偏移量始终为1
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines(): # 双层for循环逐一将每行数据,每个特征值进行添加
lineArr =[]
curLine = line.strip().split('t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
(3)计算最佳拟合参数
def standRegres(xArr,yArr):
'''计算最佳回归系数(最佳拟合直线)'''
xMat = mat(xArr); yMat = mat(yArr).T
xTx = xMat.T*xMat # X^T * X
if linalg.det(xTx) == 0.0: # 判断是否可逆
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T*yMat) # ((X^T * X)^-1) * X^T * Y
return ws
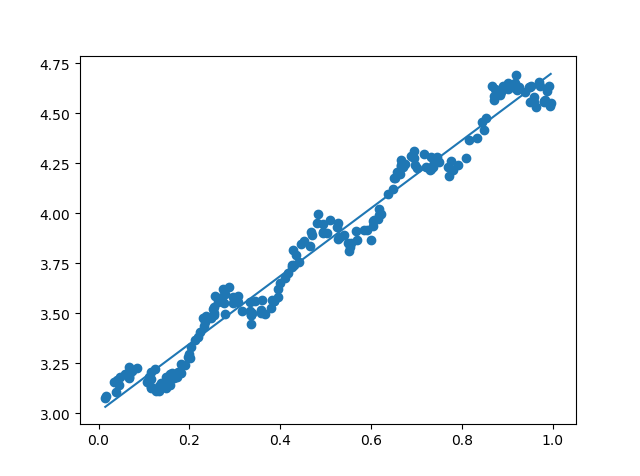
求出ws后,可用y = X * ws计算出回归的预测值,数据散点图和最佳拟合直线如下所示:
4、示例2(局部加权线性回归,Locally Weighted Linear Regression,LWLR)
局部加权作为对普通最小二乘法的一种改进方法,主要思想是将带预测点附近的每一个点赋予一定的权重,LWLR使用“核”来对附近的点赋予更高的权重,与kNN类似,加权模型认为样本点距离越近,越可能符合同一线性模型。其中最常用为高斯核,高斯核对应权重: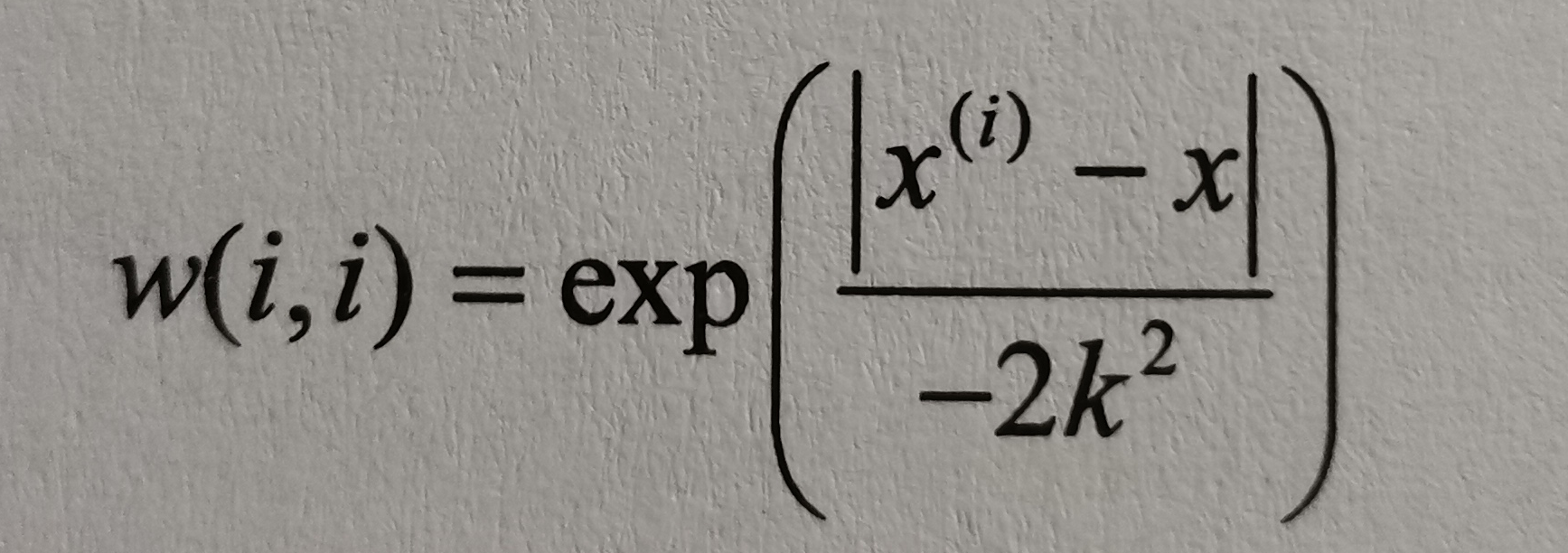
其中系数k越小,权重也越加集中在测试点附近,当k = 1.0 时效果与最小二乘法差不多。回归系数w: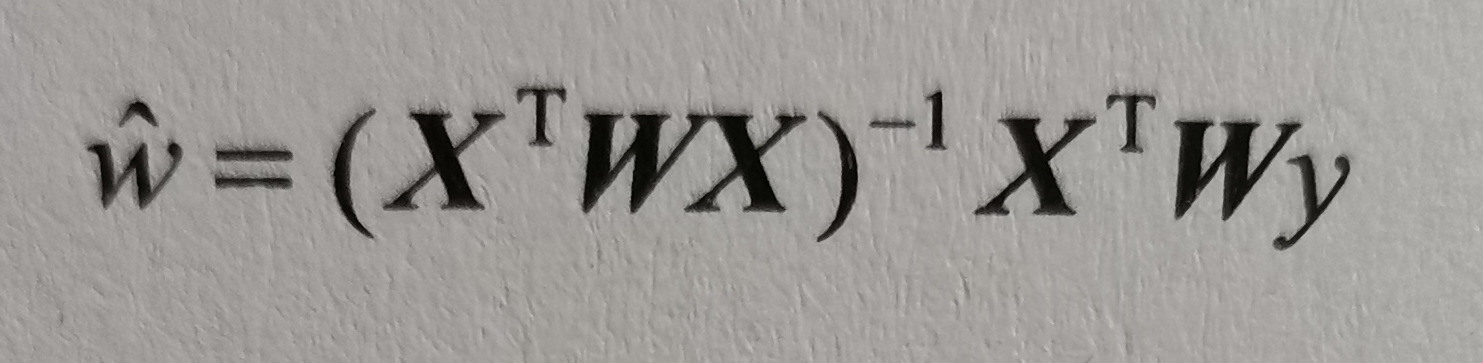
(1)局部加权线性回归
def lwlr(testPoint,xArr,yArr,k=1.0):
xMat = mat(xArr); yMat = mat(yArr).T
m = shape(xMat)[0] # m:数据总数
weights = mat(eye((m))) # eye(N),返回N*N大小的单位矩阵;
for j in range(m): # 创建权重矩阵weights
diffMat = testPoint - xMat[j,:] # x^(i) - x
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) # 带入高斯核,权重大小以指数级递减
xTx = xMat.T * (weights * xMat)
if linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * (weights * yMat))
return testPoint * ws
def lwlrTest(testArr,xArr,yArr,k=1.0): # 循环对每条数据使用
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
当k = 1.0时(underfitting)
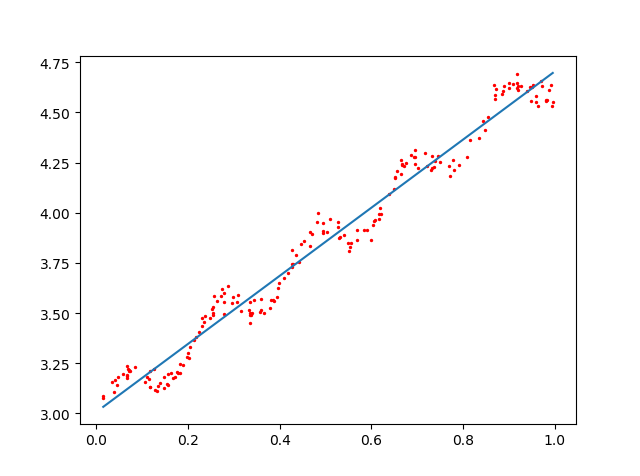
当k = 0.01时(just right)
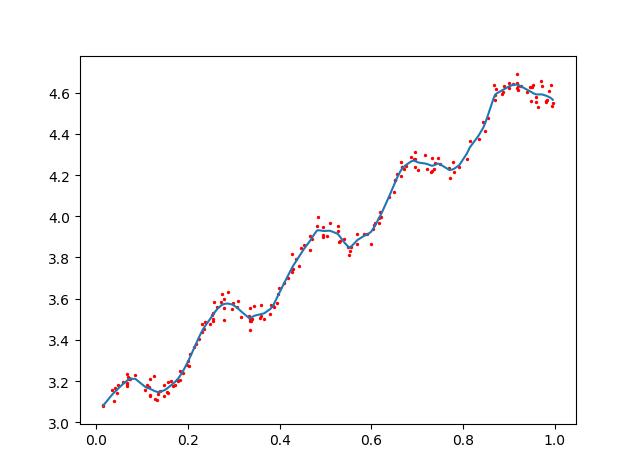 ###### 当k = 0.003时(overfitting)
###### 当k = 0.003时(overfitting)
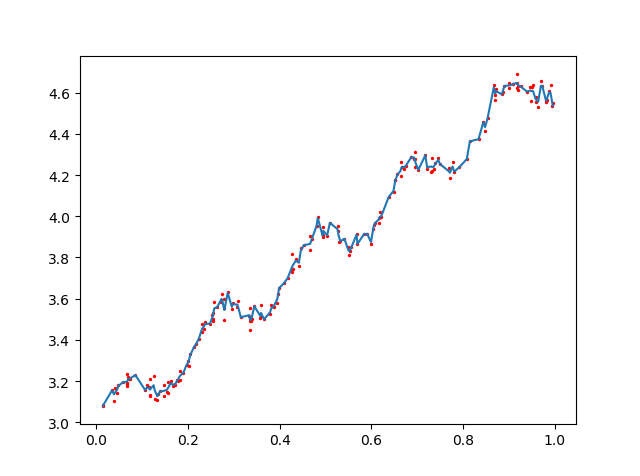
当k取值得当时,局部加权回归确实会比简单的回归表现的更好,但此回归的问题在于,每次必须在整个数据集上运行,也就是说为了作出预测,必须保持所有的训练数据。
最后
以上就是沉默秀发最近收集整理的关于机器学习实战笔记(1)机器学习实战笔记(1)的全部内容,更多相关机器学习实战笔记(1)机器学习实战笔记(1)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复