PyTorch笔记 - Convolution卷积运算的原理 (4)

unfold操作，torch.nn.Unfold

unfold = nn.Unfold(kernel_size=(2, 3))  # 6维，2x3
input = torch.randn(2, 5, 3, 4)  # 2是batch，5是input_channel，
output = unfold(input)
output.size()  # [2, 30, 4]，2x3x5=30，kernel是2x3，feature_map是3x4，(I-K+2P)/S+1 = (3-2+0)/1+1 = 2，输出是2x2的blocks=4

matrix_multiplication_for_conv2d_flatten版本，可以通过unfold实现

nn.ConvTranspose2d转置卷积

• torch.nn.ConvTranspose2d
• torch.nn.functional.conv_transpose2d

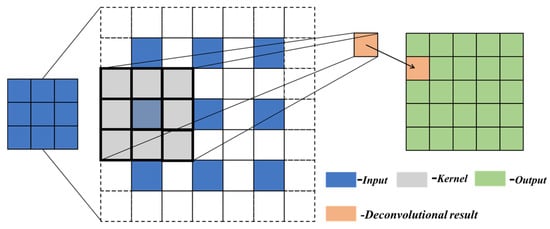
把5x5的Input转换为25x1，将3x3的kernel，也转换为25x1的kernel，其他位置进行填充0，通过kernel matrix，提升特征图尺寸

• 转置卷积用在上采样
• 后向传播实现转置卷积，或者，填充input实现转置卷积

通过对kernel进行展开，来实现二维卷积，并推导出转置卷积，不考虑batch和channel

• 可以实现卷积，降低特征图的尺寸
• 也可以实现转置卷积(ConvTranspose2d)，提升特征图的尺寸

# step4：通过对kernel进行展开，来实现二维卷积，并推导出转置卷积，不考虑batch和channel
def get_kernel_matrix(kernel, input_size, stride=1):
    """
    基于kernel和输入特征图的大小，来得到填充拉直后的kernel堆叠后的矩阵
    """
    kernel_h, kernel_w = kernel.shape
    input_h, input_w = input_size  # 元组
    output_h, output_w = int((input_h-kernel_h)/stride + 1), int((input_w-kernel_w)/stride+1)
    num_out_feat_map = output_h * output_w
    result = torch.zeros((num_out_feat_map, input_h*input_w))  # 初始化结果矩阵，输出特征图元素个数*输入特征图元素个数
    for i in range(0, output_h, stride):
        for j in range(0, output_w, stride):
            # 左右上下，填充成跟输入特征图一样的大小
            padded_kernel = F.pad(kernel, (j, input_w-kernel_w-j, i, input_h-kernel_h-i))
            result[i*output_h + j] = padded_kernel.flatten()
    return result

# 测试1：验证卷积
kernel = torch.randn(3, 3)
input = torch.randn(4, 4)
kernel_matrix = get_kernel_matrix(kernel, input.shape)  # 4x16
print(f"[Info] kernel: n{kernel}")
print(f"[Info] kernel_matrix: n{kernel_matrix}")
mm_conv2d_output = kernel_matrix @ input.reshape((-1, 1))   # 通过矩阵相乘的方式，算出卷积
mm_conv2d_output_ = mm_conv2d_output.reshape(1, 1, 2, 2)  # 对齐
print(f"[Info] mm_conv2d_output_.shape: {mm_conv2d_output_.shape}")
print(f"[Info] mm_conv2d_output_: n{mm_conv2d_output_}")
# PyTorch conv2d api
pytorch_conv2d_output = F.conv2d(input.reshape(1, 1, *input.shape), kernel.reshape(1, 1, *kernel.shape))
print(f"[Info] pytorch_conv2d_output: n{pytorch_conv2d_output}")

# 测试2：验证二维转置卷积，将输入卷积由input 2x2，ouput上升为4x4
# 通过kernel matrix，提升特征图尺寸，TransposedConv，转置卷积用在上采样
mm_transposed_conv2d_output = kernel_matrix.transpose(-1, -2) @ mm_conv2d_output
mm_transposed_conv2d_output = mm_transposed_conv2d_output.reshape(1, 1, 4, 4)
print(f"[Info] mm_transposed_conv2d_output: n{mm_transposed_conv2d_output}")

pytorch_transposed_conv2d_output = F.conv_transpose2d(pytorch_conv2d_output, kernel.reshape(1, 1, *kernel.shape))
print(f"[Info] pytorch_transposed_conv2d_output: n{pytorch_transposed_conv2d_output}")

最后

以上就是凶狠胡萝卜为你收集整理的PyTorch笔记 - Convolution卷积运算的原理 (4)的全部内容，希望文章能够帮你解决PyTorch笔记 - Convolution卷积运算的原理 (4)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。