note
- Comirec-SA基于attention的多兴趣建模,论文中先通过attention提取单一兴趣,再推广到多兴趣建模。另外使用贪心算法优化带有准确度+多样性的目标函数。
- DR把MIND的attention换成argmax(还有初始化方式不同、序列胶囊到兴趣胶囊用可学习权重矩阵替代的不同),SR则本质是多头注意力进行多兴趣建模。
torch.einsum(Einstein summation convention,即爱因斯坦求和约定)可以写tensor运算和更高维度tensor写法更加简洁,如用torch.einsum("bij, bjk -> bik", batch_tensor_1, batch_tensor_2)进行batch内矩阵乘法运算。- 注意力机制中最后对第一个维度
seq进行sofjtmax归一化,即使得seq维度的元素之和为1。因为对于固定序列中不存在的位置负无穷mask掉了,所以缺失的位置经过softmax归一化后的数值为0。 Softmax ( x i ) = exp ( x i ) ∑ j exp ( x j ) operatorname{Softmax}left(x_iright)=frac{exp left(x_iright)}{sum_j exp left(x_jright)} Softmax(xi)=∑jexp(xj)exp(xi)
文章目录
- note
- 一、Comirec模型概览
- 1.1 Notation
- 1.2 模型框架
- 1.3 model training
- 二、Comirec-SA模型
- 2.0 数据集划分
- 2.1 基于Attention的单一兴趣建模
- 2.2 基于Attention的多兴趣建模
- (1)K-Q-V注意力
- 1)自注意力机制
- 2)计算 K-Q-V 注意力(矩阵形式):
- 2.3 多样性控制
- 三、代码实践
- 3.1 MultiInterest_SA类定义
- 3.2 einsum函数的用法
- 3.3 Comirec-SA类定义
- 时间安排
- Reference
一、Comirec模型概览
第一部分和task5差不多,是同一篇论文Comirec-SA用self-attentive method代替之前DR多兴趣抽取层,

Comirec:Controllable Multi-Interest Framework for Recommendation
论文链接:https://arxiv.org/abs/2005.09347
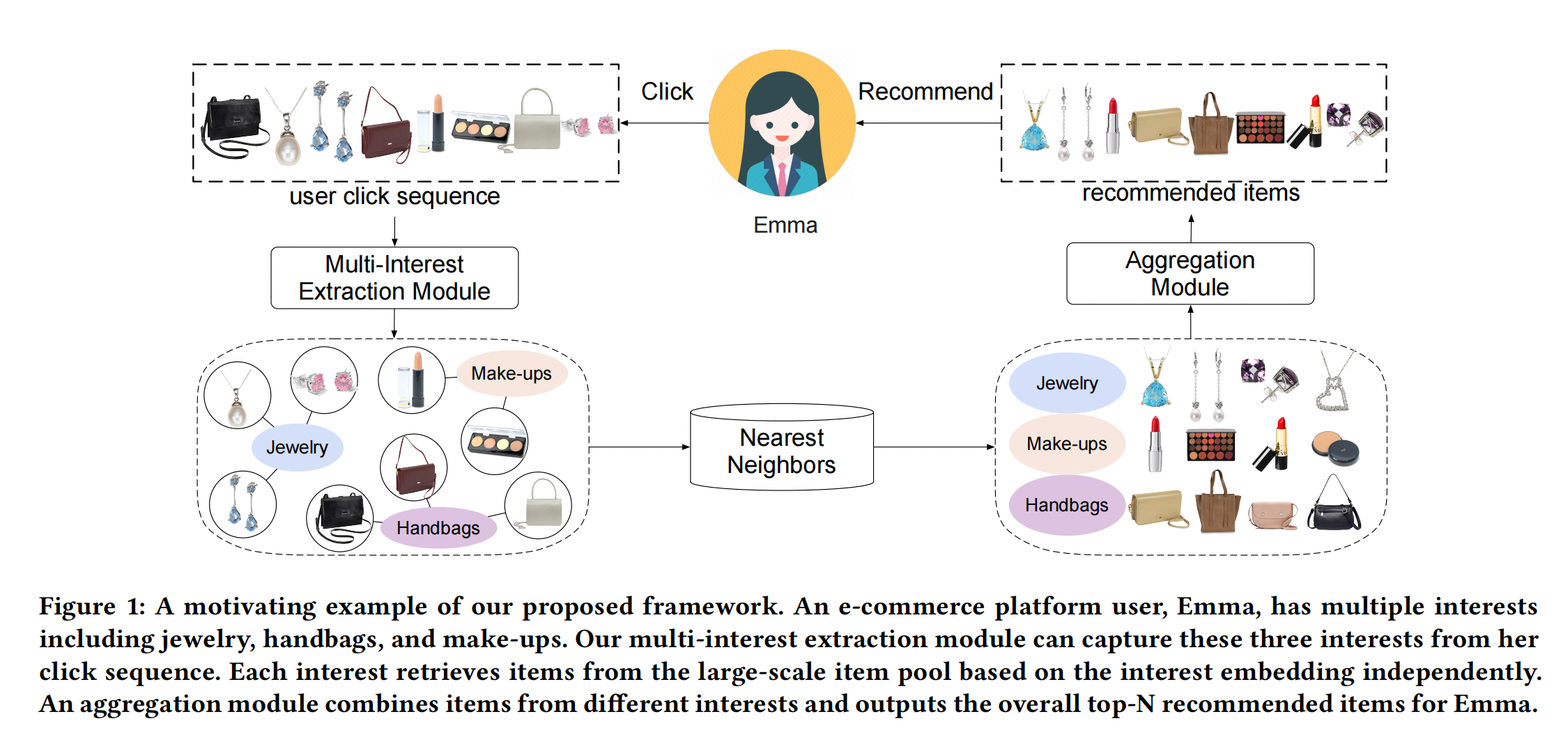
Comirec是阿里发表在KDD 2020上的一篇工作,这篇论文对MIND多行为召回进行了扩展:
- 一方面改进了MIND中的动态路由算法,
- 另一方面提出了一种新的多兴趣召回方法,同时对推荐的多样性层面也做出了一定的贡献,通过一种贪心的做法,在损失较小的推荐效果的情况下可以显著的提高推荐的多样性(感觉非常非常牵强,我们这里就不介绍这个了),从而极大的提高用户的使用体验,可以更进一步的探索用户的潜在兴趣。
1.1 Notation
假设一个用户集合 u ∈ U u in mathcal{U} u∈U 和一个物品集合 i ∈ I i in mathcal{I} i∈I, 对于每一个用户, 定义用户序列 ( e 1 ( u ) , e 2 ( u ) , … , e n ( u ) ) left(e_1^{(u)}, e_2^{(u)}, ldots, e_n^{(u)}right) (e1(u),e2(u),…,en(u)), 根据时间先后顺序排序,其中 e t ( u ) e_t^{(u)} et(u) 记录了第 t t t 个物品与用户交互。
1.2 模型框架
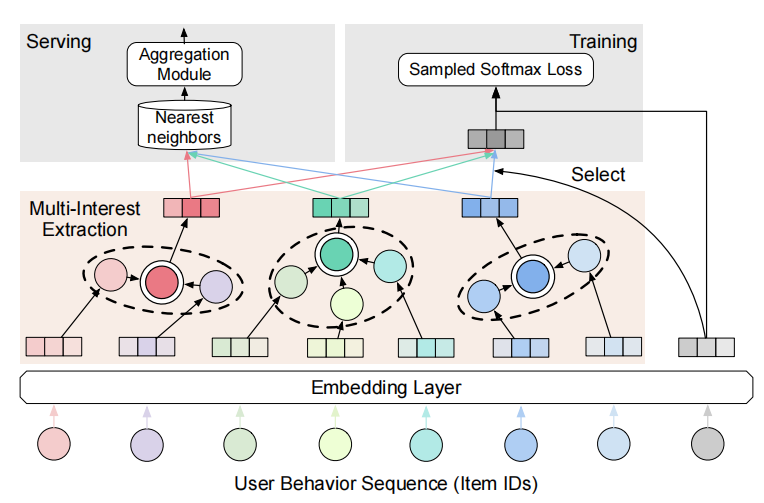
Comirec流程:
- 用户历史交互item ids经过embedding layer转为item embeddings;
- 把刚才的item embedding经过多兴趣抽取层(这里是
self-attentive模块),得到K个interest embeddings; - training:和之前MIND说的做法一样(取内积最大值),即选出与target item embedding最接近的interest embeddings,基于多分类任务,使用负采样sampled softmax loss;
- serving(predict):对于每个用户的K个interest embedding进行top-N检索,即召回
K X N个item。 - aggregation module:将
K X N个item送入该模块得到N个item(选内积分数最高的N个,和MIND做法一致): f ( u , i ) = max 1 ≤ k ≤ K ( e i ⊤ v u ( k ) ) f(u, i)=max _{1 leq k leq K}left(mathbf{e}_i^{top} mathbf{v}_u^{(k)}right) f(u,i)=1≤k≤Kmax(ei⊤vu(k))
1.3 model training
和1.1说的一样,某用户经过多兴趣提取层后得到K个interest embeddings后,从中找出和target item i(即下面embedding为
e
i
e_i
ei)最接近,即内积最大的一个interest embeeding,方法如下
v
u
=
V
u
[
:
,
argmax
(
V
u
⊤
e
i
)
]
,
mathbf{v}_u=mathbf{V}_uleft[:, operatorname{argmax}left(mathbf{V}_u^{top} mathbf{e}_iright)right],
vu=Vu[:,argmax(Vu⊤ei)],
和之前一样是结合负采样的最大似然法(后面代码用少量数据,直接交叉熵损失函数)。给出一个训练样本
(
u
,
i
)
(u, i)
(u,i), 用户embedding
v
u
mathbf{v}_u
vu, 和物品embedding
e
i
mathbf{e}_i
ei,则用户与物品交互的似然函数:
P
θ
(
i
∣
u
)
=
exp
(
v
u
⊤
e
i
)
∑
k
∈
I
exp
(
v
u
⊤
e
k
)
P_theta(i mid u)=frac{exp left(mathbf{v}_u^{top} mathbf{e}_iright)}{sum_{k in I} exp left(mathbf{v}_u^{top} mathbf{e}_kright)}
Pθ(i∣u)=∑k∈Iexp(vu⊤ek)exp(vu⊤ei)
目标为最小化该似然函数:
loss
=
∑
u
∈
U
∑
i
∈
I
u
−
log
P
θ
(
i
∣
u
)
text { loss }=sum_{u in mathcal{U}} sum_{i in I_u}-log P_theta(i mid u)
loss =u∈U∑i∈Iu∑−logPθ(i∣u)
二、Comirec-SA模型
2.0 数据集划分
原论文是按照8:1:1划分训练集、验证集、测试集(按照用户划分,更具泛化能力)。
- 训练样本:全部点击序列 ( e 1 ( u ) , e 2 ( u ) , … , e k ( u ) , … , e n ( u ) ) left(e_1^{(u)}, e_2^{(u)}, ldots, e_k^{(u)}, ldots, e_n^{(u)}right) (e1(u),e2(u),…,ek(u),…,en(u)),用前(n-1)个item预测第n个;
- 验证集合测试集则是使用用户前80%的点击序列作为模型输入,然后预测后面的点击序列。
- 在验证集合测试集中的用户是从未在训练集中出现过的。
2.1 基于Attention的单一兴趣建模
- 将用户的行为序列计作
H
∈
R
d
×
n
H in mathbb{R}^{d times n}
H∈Rd×n,
- 这里的 n n n 表示用户行为序列的长度,
- d d d 表示Embedding向量的维度,
- 这里的 H H H 就代表着用户行为序列中所有Item的Embedding向量,
- 这里引入两个可学习参数 W 1 ∈ R d a × d , w 2 ∈ R d a W_1 in mathbb{R}^{d_a times d}, w_2 in mathbb{R}^{d_a} W1∈Rda×d,w2∈Rda, 通过引入Attention机制进行加权求和,凸显重要性高的特征。
在我们的Comirec-SA中, 我们的特征重要性 (也就是我们学习出来的Attention Score) 是针对序列中每个Item的Attention Score, 在有了Attention Score之后就可以对序列中的|tem进行加权求和得到序列的单一兴趣表征了。单一兴趣建模时的Attention Score计算:
a
=
softmax
(
w
2
T
tanh
(
W
1
H
)
)
T
a=operatorname{softmax}left(w_2^T tanh left(W_1 Hright)right)^T
a=softmax(w2Ttanh(W1H))T
- a ∈ R n a in mathbb{R}^n a∈Rn, 这里的 a a a 就是我们对序列的Attention Score(权重向量), 再将 a a a 与序列的所有Item的Embedding进行加权求和就可以得到单一兴趣的建模。
2.2 基于Attention的多兴趣建模
可以把 1.1 1.1 1.1单一兴趣建模中的 w 2 ∈ R d a w_2 in mathbb{R}^{d_a} w2∈Rda 扩充至 W 2 ∈ R d a × K W_2 in mathbb{R}^{d_a times K} W2∈Rda×K(可训练化参数), 这里是因为在输入embedding中加入了可训练的position embedding,其维度和item embedding的维度一样都是 d d d。
Attention Score的计算公式就变成:
A
=
softmax
(
W
2
T
tanh
(
W
1
H
)
)
T
A=operatorname{softmax}left(W_2^T tanh left(W_1 Hright)right)^T
A=softmax(W2Ttanh(W1H))T
其中:
- A ∈ R n × K A in mathbb{R}^{n times K} A∈Rn×K,
- 权重 W 2 ∈ R d a × K W_2 in mathbb{R}^{d_a times K} W2∈Rda×K
- K是兴趣向量个数
这时我们可以通过如下式子得到用户的多兴趣表征:
V
u
=
H
A
V_u=H A
Vu=HA
其中:
- H d × n mathbf{H}^{d times n} Hd×n:用户行为序列的embedding矩阵,其中 n n n为用户行为序列的长度, d d d为item embedding维度;
- V u ∈ R d × K V_u in mathbb{R}^{d times K} Vu∈Rd×K, 即为 K mathrm{K} K 个兴趣表征, 其核心代码如下:
class MultiInterest_SA(nn.Layer):
def __init__(self, embedding_dim, interest_num, d=None):
super(MultiInterest_SA, self).__init__()
self.embedding_dim = embedding_dim
self.interest_num = interest_num
if d == None:
self.d = self.embedding_dim*4
self.W1 = self.create_parameter(shape=[self.embedding_dim, self.d])
self.W2 = self.create_parameter(shape=[self.d, self.interest_num])
def forward(self, seq_emb, mask = None):
'''
seq_emb : batch,seq,emb
mask : batch,seq,1
'''
H = paddle.einsum('bse, ed -> bsd', seq_emb, self.W1).tanh()
mask = mask.unsqueeze(-1)
A = paddle.einsum('bsd, dk -> bsk', H, self.W2) + -1.e9 * (1 - mask)
A = F.softmax(A, axis=1)
A = paddle.transpose(A,perm=[0, 2, 1])
multi_interest_emb = paddle.matmul(A, seq_emb)
return multi_interest_emb
首先来回顾单头和多头的注意力:
(1)K-Q-V注意力
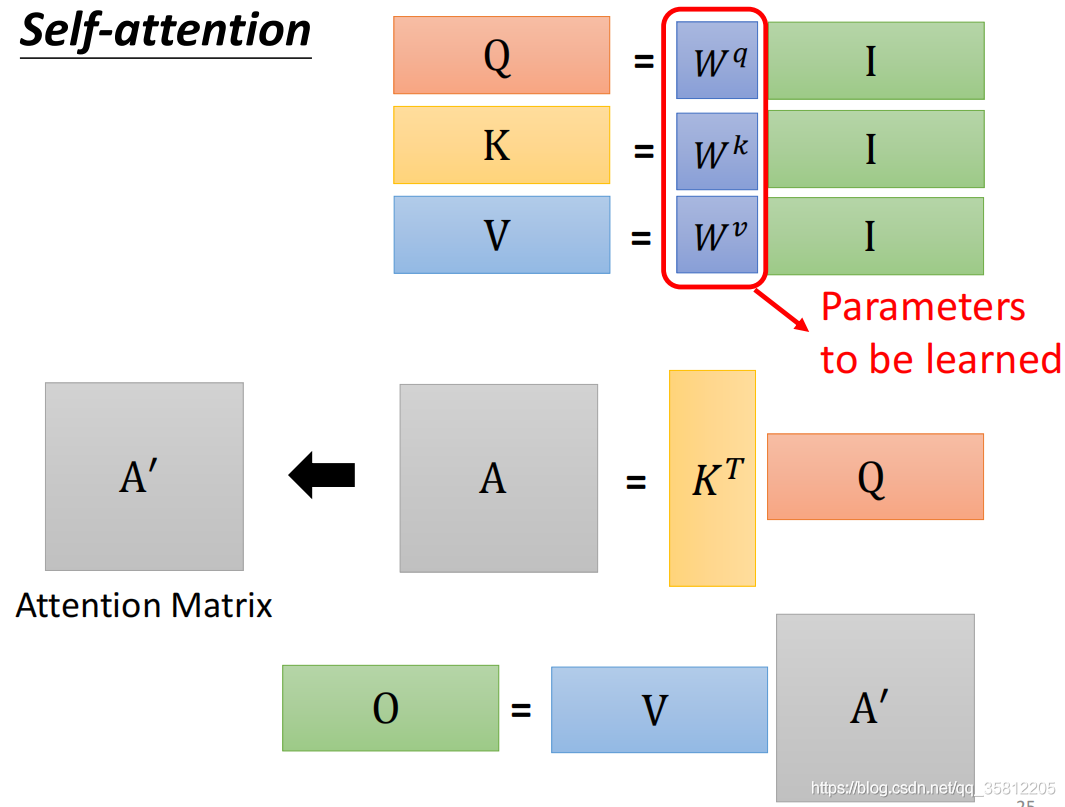
1)自注意力机制
自注意力是指键(K)、查询(Q)和值(V)来自同一数据来源,即 K=Q=V。
Transformer 以特定方式执行此操作:
令
x
1
,
x
2
,
⋯
,
x
T
x_{1}, x_{2}, cdots, x_{T}
x1,x2,⋯,xT 是 Transformer 编码器的输入向量, 其中
x
i
∈
R
d
x_{i} in R^{d}
xi∈Rd, 则键
(
K
)
(K)
(K) 、查询
(
Q
)
(Q)
(Q) 、值
(
V
)
(V)
(V) 是:
k
i
=
K
x
i
q
i
=
Q
x
i
v
i
=
V
x
i
begin{aligned} k_{i} &=K x_{i} \ q_{i} &=Q x_{i} \ v_{i} &=V x_{i} end{aligned}
kiqivi=Kxi=Qxi=Vxi
- 其中: 矩阵 K ∈ R d × d ; Q ∈ R d × d ; V ∈ R d × d K in R^{d times d} ; Q in R^{d times d} ; V in R^{d times d} K∈Rd×d;Q∈Rd×d;V∈Rd×d 。
- 这些矩阵允许将x向量的不同方面用于三个角色的每一个。
2)计算 K-Q-V 注意力(矩阵形式):
令 X = [ x 1 , x 2 , ⋯ , x T ] ∈ R T × d mathrm{X}=left[x_{1}, x_{2}, cdots, x_{T}right] in mathrm{R}^{mathrm{T} times mathrm{d}} X=[x1,x2,⋯,xT]∈RT×d 是输入向量的串联(拼接), 其中:
- X K ∈ R T × d , X Q ∈ R T × d , X V ∈ R T × d X K in R^{T times d}, X Q in R^{T times d}, X V in R^{T times d} XK∈RT×d,XQ∈RT×d,XV∈RT×d 。
- 输出定义为: output = softmax ( X Q ( X K ) T × X V ) operatorname{softmax}left(X Q(X K)^{mathrm{T}} times X Vright) softmax(XQ(XK)T×XV)
- 即计算过程:首先, 在一个矩阵乘法中取查询和键的点积, 得到: X Q ( X K ) T X Q(X K)^{mathrm{T}} XQ(XK)T;其次, 对上述结果进行 softmax 计算, 再乘以矩阵 X V X V XV, 得到: softmax ( X Q ( X K ) T ) × X V operatorname{softmax}left(X Q(X K)^{mathrm{T}}right) times X V softmax(XQ(XK)T)×XV ,如下图的(a)。
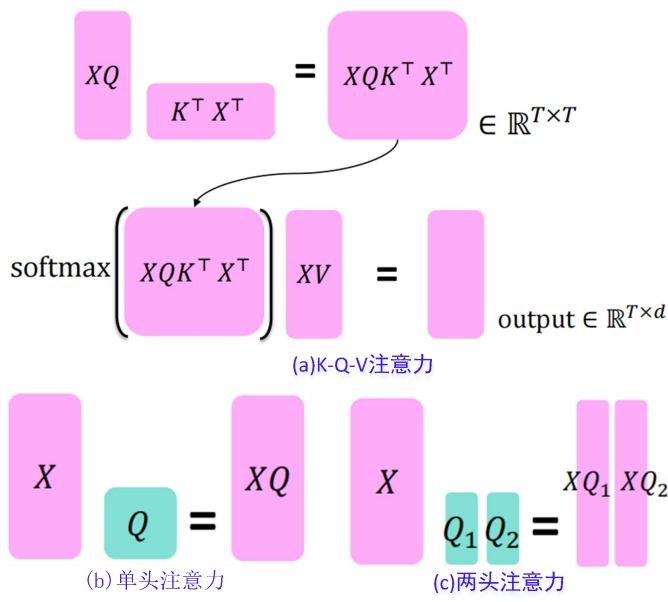
如果想一次查询(Q)句子中的多个位置:
对于单词
i
mathrm{i}
i, self-attention 只 “看”
x
i
T
Q
T
K
x
j
x_{i}^{T} Q^{T} K x_{j}
xiTQTKxj 分数高的地方, 即单头注意力, 见上图的(b) 。但是, 若出于不同的原因想要关注不同的
j
mathrm{j}
j,则可通过多个
Q
、
K
、
V
mathrm{Q} 、 mathrm{~K} 、 mathrm{~V}
Q、 K、 V 矩阵来定义多个注意力 “头”:
令: Q l , K l , V l ∈ R d × d / h Q_{l}, K_{l}, V_{l} in R^{d times d / h} Ql,Kl,Vl∈Rd×d/h, 其中 h h h 是注意力头的数量, l l l 的范围从 1 到 h h h,则: 每个注意力头独立地计算注意力: output l = softmax ( X Q l K l T X T ) ∗ X V l text { output }_{l}=operatorname{softmax}left(X Q_{l} K_{l}^{T} X^{T}right) * X V_{l} output l=softmax(XQlKlTXT)∗XVl
其中:output l ∈ R d / h _{l} in R^{d / h} l∈Rd/h
然后合并所有头的输出: output = Y [output 1 , … , output h ] text { output }=Y text { [output }_{1}, ldots, text { output }_{h} text { ] } output =Y [output 1,…, output h ]
其中: Y ∈ R d × d Y in R^{d times d} Y∈Rd×d
因此, 每个头都可以 “看” 不同的事物, 并以不同的方式构建值 ( V mathrm{V} V ) 向量。多头注意力和单头自注意力有相同的计算量。最简单的多头注意力,即两头注意力(如上图的c)。
2.3 多样性控制
为了强化推荐item的多样性,作者将item的类别作为衡量多样性的基础。
问题定义:给定从用户 u u u 的 K K K 个兴趣中检索到一个集合 M mathcal{M} M, 有 K ⋅ N K cdot N K⋅N 个物品, 找到一个输出集合 S mathcal{S} S, 有 N N N 个 物品 (Top-N) , 使预定义的值函数 Q ( u , S ) Q(u, mathcal{S}) Q(u,S)最大化。
(1)多样性:作者使用
g
(
i
,
j
)
g(i, j)
g(i,j)用来衡量两个Item i, j之间的多样性:
g
(
i
,
j
)
=
σ
(
C
A
T
E
(
i
)
≠
C
A
T
E
(
j
)
)
g(i, j)=sigma(C A T E(i) neq C A T E(j))
g(i,j)=σ(CATE(i)=CATE(j))
- C A T E ( i ) C A T E(i) CATE(i) 表示物品 i i i 的类别
- σ sigma σ 为指示函数,这里就是如果两个item的类别不相同,那么其结果就是 1 , 反之就是 0
- 可以看出如果一个推荐集合中两两Item的多样性得分大的话, 那么可以认为这个推荐结果中的Item的类别分布较为分散, 也就可以认为推荐结果的多样性较高了,
(2)推荐精度:当推荐结果的多样性较高的时候, 往往推荐的精度就会下降, 这是一个Trade Off,可以构造如下的目标函数(包含多样性指标和推荐精度指标): Q ( u , S ) = ∑ i ∈ S f ( u , i ) + λ ∑ i ∈ S ∑ j ∈ S g ( i , j ) Q(u, mathcal{S})=sum_{i in mathcal{S}} f(u, i)+lambda sum_{i in mathcal{S}} sum_{j in mathcal{S}} g(i, j) Q(u,S)=i∈S∑f(u,i)+λi∈S∑j∈S∑g(i,j)
- 通过 λ lambda λ 来控制这两部分的占比, λ lambda λ 越大则多样性更强,同事准确度会降低;
- 作者这里提出使用一种贪心的做法来进行目标函数的优化, 优化流程如下:

三、代码实践
3.1 MultiInterest_SA类定义
如上面介绍的SA运算:
A
=
softmax
(
W
2
T
tanh
(
W
1
H
)
)
T
A=operatorname{softmax}left(W_2^T tanh left(W_1 Hright)right)^T
A=softmax(W2Ttanh(W1H))T
可以得到
A
∈
R
n
×
K
A in mathbb{R}^{n times K}
A∈Rn×K, 这时我们可以通过如下式子得到用户的多兴趣表征:
V
u
=
H
A
V_u=H A
Vu=HA
注意:
- 两个维度不同的tensor也可以“做加减法”(指的是代码中的写法), 比如
[256, 20, 4]的tensor-[256, 20, 1]的tensor,后者会减在全部(4个)第2维度之上。 - 下面这里的
paddle.einsum函数在tf和torch中都有,einsum(Einstein summation convention,即爱因斯坦求和约定)可以写tensor运算和更高维度tensor写法更加简洁。torch版本的多兴趣抽取层SA代码如下。 - 最后对第一个维度
seq进行sofjtmax归一化,即使得seq维度的元素之和为1。因为对于固定序列中不存在的位置负无穷mask掉了,所以缺失的位置经过softmax归一化后的数值为0。 Softmax ( x i ) = exp ( x i ) ∑ j exp ( x j ) operatorname{Softmax}left(x_iright)=frac{exp left(x_iright)}{sum_j exp left(x_jright)} Softmax(xi)=∑jexp(xj)exp(xi)
class MultiInterest_SA(nn.Module):
def __init__(self, embedding_dim, interest_num, d=None):
super(MultiInterest_SA, self).__init__()
self.embedding_dim = embedding_dim
self.interest_num = interest_num
if d == None:
self.d = self.embedding_dim*4
# self.W1 = self.create_parameter(shape=[self.embedding_dim, self.d])
# self.W2 = self.create_parameter(shape=[self.d, self.interest_num])
self.W1 = Parameter(torch.Tensor(self.embedding_dim, self.d))
self.W2 = Parameter(torch.Tensor(self.d, self.interest_num))
def forward(self, seq_emb, mask = None):
'''
seq_emb : batch,seq,emb
mask : batch,seq,1
'''
H = torch.einsum('bse, ed -> bsd', seq_emb, self.W1).tanh()
mask = mask.unsqueeze(-1) # (batch, seq) -> (batch, seq, 1)
# einsum 爱因斯坦求和约定
# (batch_size, seq_len, interest_num) - (batch_size, seq_len, 1)负无穷,
# 两个维度不同可以做减法, 比如[256, 20, 4]-[256, 20, 1],后者会减在4个 全部之上
A = torch.einsum('bsd, dk -> bsk', H, self.W2) + -1.e9 * (1 - mask)
A = F.softmax(A, dim=1)
A = torch.transpose(A, 2, 1)
multi_interest_emb = torch.matmul(A, seq_emb)
return multi_interest_emb
3.2 einsum函数的用法
einsum(Einstein summation convention,即爱因斯坦求和约定)的用法:
- c i k = ∑ j a i j b j k c_{i k}=sum_j a_{i j} b_{j k} cik=∑jaijbjk 的写法如下:
c = np.dot(a, b) # 常规
c = np.einsum('ij,jk->ik', a, b) # einsum
- 再比如
c
k
l
=
∑
i
∑
j
a
i
j
k
b
i
j
l
c_{mathrm{kl}}=sum_{mathrm{i}} sum_{mathrm{j}} mathrm{a}_{mathrm{ijk}} mathrm{b}_{mathrm{ijl}}
ckl=∑i∑jaijkbijl :
c = np.einsum('ijk,jkl->kl', a, b)
import torch
# 1. 张量转置
A = torch.randn(3, 4, 5)
B = torch.einsum("ijk->ikj", A)
print(A.shape, "n", B.shape, "n", "======") # (3, 4, 5) ; (3, 5, 4)
# 2. 取对角元素
A = torch.randn(5, 5)
B = torch.einsum("ii->i", A)
print(A.shape, "n", B.shape, "n", "======")
# 3. 求和降维
A = torch.randn(4, 5)
B = torch.einsum("ij->i", A)
print(A.shape, "n", B.shape, "n", "======")
# 4. 哈达玛积(两个矩阵维度相同)
A = torch.randn(3, 4)
B = torch.randn(3, 4)
C = torch.einsum("ij, ij->ij", A, B)
print(A.shape, "n", B.shape, "n", C.shape, "n", "======")
# 5. 向量内积
A = torch.randn(10)
B = torch.randn(10)
#C=torch.dot(A,B)
C = torch.einsum("i,i->",A,B)
# 6. 向量外积
A = torch.randn(10)
B = torch.randn(5)
#C = torch.outer(A,B)
C = torch.einsum("i,j->ij",A,B)
# 7. 矩阵乘法
A = torch.randn(5,4)
B = torch.randn(4,6)
#C = torch.matmul(A,B)
C = torch.einsum("ik,kj->ij",A,B)
# 8. 张量缩并
A = torch.randn(3,4,5)
B = torch.randn(4,3,6)
#C = torch.tensordot(A,B,dims=[(0,1),(1,0)])
C = torch.einsum("ijk,jih->kh",A,B)
# 9. batch矩阵乘法
batch_tensor_1 = torch.arange(2 * 4 * 3).reshape(2, 4, 3)
batch_tensor_2 = torch.arange(2 * 3 * 4).reshape(2, 3, 4)
torch.bmm(batch_tensor_1, batch_tensor_2) # [2, 4, 4]
torch.einsum("bij, bjk -> bik", batch_tensor_1, batch_tensor_2) # [2, 4, 4]
3.3 Comirec-SA类定义
这部分和之前DR的类时一样的,改动的部分都体现在MultiInterest_SA上了。
class ComirecSA(nn.Layer):
def __init__(self, config):
super(ComirecSA, self).__init__()
self.config = config
self.embedding_dim = self.config['embedding_dim']
self.max_length = self.config['max_length']
self.n_items = self.config['n_items']
self.item_emb = nn.Embedding(self.n_items, self.embedding_dim, padding_idx=0)
self.multi_interest_layer = MultiInterest_SA(self.embedding_dim,interest_num=self.config['K'])
self.loss_fun = nn.CrossEntropyLoss()
self.reset_parameters()
def calculate_loss(self,user_emb,pos_item):
all_items = self.item_emb.weight
scores = paddle.matmul(user_emb, all_items.transpose([1, 0]))
return self.loss_fun(scores,pos_item)
def output_items(self):
return self.item_emb.weight
def reset_parameters(self, initializer=None):
for weight in self.parameters():
paddle.nn.initializer.KaimingNormal(weight)
def forward(self, item_seq, mask, item, train=True):
if train:
seq_emb = self.item_emb(item_seq) # Batch,Seq,Emb
item_e = self.item_emb(item).squeeze(1)
multi_interest_emb = self.multi_interest_layer(seq_emb, mask) # Batch,K,Emb
cos_res = paddle.bmm(multi_interest_emb, item_e.squeeze(1).unsqueeze(-1))
k_index = paddle.argmax(cos_res, axis=1)
best_interest_emb = paddle.rand((multi_interest_emb.shape[0], multi_interest_emb.shape[2]))
for k in range(multi_interest_emb.shape[0]):
best_interest_emb[k, :] = multi_interest_emb[k, k_index[k], :]
loss = self.calculate_loss(best_interest_emb,item)
output_dict = {
'user_emb': multi_interest_emb,
'loss': loss,
}
else:
seq_emb = self.item_emb(item_seq) # Batch,Seq,Emb
multi_interest_emb = self.multi_interest_layer(seq_emb, mask) # Batch,K,Emb
output_dict = {
'user_emb': multi_interest_emb,
}
return output_dict
时间安排
| 任务信息 | 截止时间 | 完成情况 |
|---|---|---|
| 11月14日周一正式开始 | ||
| Task01:Paddle开发深度学习模型快速入门 | 11月14、15、16日周三 | 完成 |
| Task02:传统序列召回实践:GRU4Rec | 11月17、18、19日周六 | 完成 |
| Task03:GNN在召回中的应用:SR-GNN | 11月20、21、22日周二 | 完成 |
| Task04:多兴趣召回实践:MIND | 11月23、24、25、26日周六 | 完成 |
| Task05:多兴趣召回实践:Comirec-DR | 11月27、28日周一 | 完成 |
| Task06:多兴趣召回实践:Comirec-SA | 11月29日周二 | 完成 |
Reference
[1] 多兴趣召回实践:Comirec-SA
论文:Controllable Multi-Interest Framework for Recommendation
链接:https://arxiv.org/abs/2005.09347
[2] 推荐场景中召回模型的演化过程. 京东大佬
[3] 原论文作者代码:https://github.com/THUDM/ComiRec/blob/a576eed8b605a531f2971136ce6ae87739d47693/src/train.py
[4] https://github.com/ShiningCosmos/pytorch_ComiRec/blob/main/ComiRec.py
[5] https://wangxiaocs.github.io/
[6] 推荐算法炼丹笔记:阿里序列化推荐算法ComiRec
[7] einsum is all you needed
[8] Understanding PyTorch einsum
[9] 矩阵操作万能函数 einsum 详细解析(通法教你如何看懂并写出einsum表达式)
[10] Sparse-Interest Network for Sequential Recommendation .AAAI 2021
[11] torch_rechub代码复现:https://github.com/datawhalechina/torch-rechub/blob/main/torch_rechub/models/matching/comirec.py
单头注意力机制:
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
Q
K
T
d
k
∗
V
Attention(Q,K,V)=frac{QK^T}{sqrt{d_k}}*V
Attention(Q,K,V)=dkQKT∗V
多头注意力机制:
M
u
l
t
i
H
e
a
d
(
Q
,
K
,
V
)
=
C
o
n
c
a
t
(
h
e
a
d
1
,
.
.
.
,
h
e
a
d
h
)
∗
W
O
MultiHead(Q,K,V)=Concat(head_1,...,head_h)*W^O
MultiHead(Q,K,V)=Concat(head1,...,headh)∗WO
其中:
h
e
a
d
i
=
A
t
t
e
n
t
i
o
n
(
Q
∗
W
i
Q
,
K
∗
W
i
K
,
V
∗
W
i
V
)
head_i=Attention(Q*W_i^Q,K*W_i^K,V*W_i^V)
headi=Attention(Q∗WiQ,K∗WiK,V∗WiV)
最后
以上就是纯真柜子最近收集整理的关于【序列召回推荐】(task6)多兴趣召回Comirec-SAnote一、Comirec模型概览二、Comirec-SA模型三、代码实践时间安排Reference的全部内容,更多相关【序列召回推荐】(task6)多兴趣召回Comirec-SAnote一、Comirec模型概览二、Comirec-SA模型三、代码实践时间安排Reference内容请搜索靠谱客的其他文章。








发表评论 取消回复