爱因斯坦求和~enisum~以及各种矩阵乘法product公式~最后有手绘enisum理解

68 阅读 0 评论 45 点赞

我是靠谱客的博主活泼大神，最近开发中收集的这篇文章主要介绍爱因斯坦求和~enisum~以及各种矩阵乘法product公式~最后有手绘enisum理解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

various product

dot product
element-wise product
inner product
outer product
Kronecker product(克罗内克积)
torch.enisumEinstein notation

1 dot product

线代中的矩阵乘法，A.dot(B)，表示A的行乘以B的列，A的列数需要等于B的行数。

$={begin{pmatrix}a_{11}&a_{12}&cdots &a_{1n}\a_{21}&a_{22}&cdots &a_{2n}\vdots &vdots &ddots &vdots \a_{m1}&a_{m2}&cdots &a_{mn}\end{pmatrix}},quad mathbf {B} ={begin{pmatrix}b_{11}&b_{12}&cdots &b_{1p}\b_{21}&b_{22}&cdots &b_{2p}\vdots &vdots &ddots &vdots \b_{n1}&b_{n2}&cdots &b_{np}\end{pmatrix}}}$

$={begin{pmatrix}c_{11}&c_{12}&cdots &c_{1p}\c_{21}&c_{22}&cdots &c_{2p}\vdots &vdots &ddots &vdots \c_{m1}&c_{m2}&cdots &c_{mp}\end{pmatrix}}}$

$c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+cdots +a_{in}b_{nj}=sum _{k=1}^{n}a_{ik}b_{kj},}$

2 element-wise product

矩阵的形状需要一致，表示前后对应坐标的元素相乘得到的矩阵

$B)_{ij}=(Aodot B)_{ij}=(A)_{ij}(B)_{ij}.}$

${begin{bmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{bmatrix}}circ {begin{bmatrix}b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33}end{bmatrix}}={begin{bmatrix}a_{11},b_{11}&a_{12},b_{12}&a_{13},b_{13}\a_{21},b_{21}&a_{22},b_{22}&a_{23},b_{23}\a_{31},b_{31}&a_{32},b_{32}&a_{33},b_{33}end{bmatrix}}.}$

3 inner product

向量的内积，即点乘，结果是一个标量（scalar）。

$^{textsf {T}}mathbf {v} }$

4 outer product

向量的外积，即叉乘，结果是一个向量（vector）。

$)_{ij}=u_{i}v_{j}}$

$^{textsf {T}}={begin{bmatrix}u_{1}\u_{2}\u_{3}\u_{4}end{bmatrix}}{begin{bmatrix}v_{1}&v_{2}&v_{3}end{bmatrix}}={begin{bmatrix}u_{1}v_{1}&u_{1}v_{2}&u_{1}v_{3}\u_{2}v_{1}&u_{2}v_{2}&u_{2}v_{3}\u_{3}v_{1}&u_{3}v_{2}&u_{3}v_{3}\u_{4}v_{1}&u_{4}v_{2}&u_{4}v_{3}end{bmatrix}}.}$

5 Kronecker product(克罗内克积)

对应维度两两相乘，如下例子， $a_{11}$ 分别与 $b_{11}、b_{21}$ 相乘为纵向前两个元素，分别与 $b_{11}、b_{12}、b_{13}$ 相乘为横向前三个元素
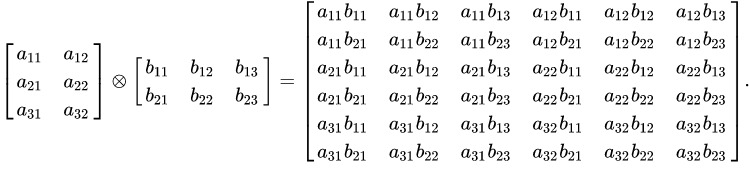
在这里插入图片描述

6 爱因斯坦求和

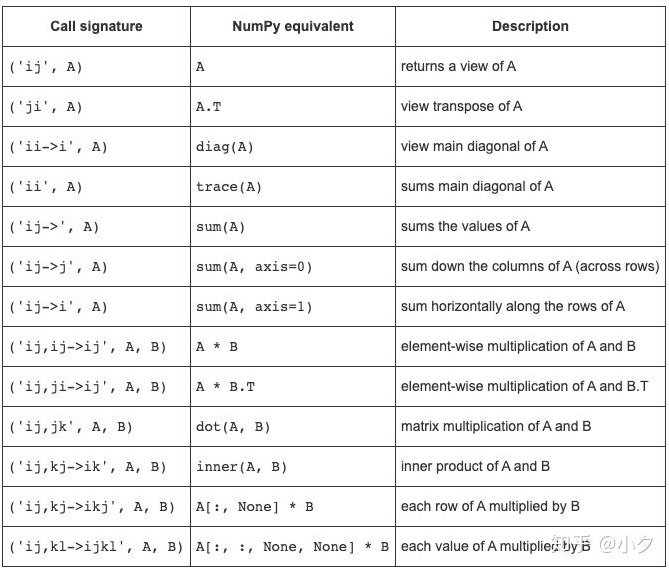
用字母标记待操作的向量或矩阵的维度，并用相应的字母标记需要的结果，中间用箭头连接。爱因斯坦求和相当于是一个矩阵处理的接口，可以计算矩阵的迹、对角矩阵、求和、点乘等等。“输入标记中重复字母表示沿这些轴的值将相乘”，“输出标记中省略字母表示沿该轴的值将被求和”

np.einsum('ij,jk->ik', A, B)可以看作是：2D矩阵乘法：
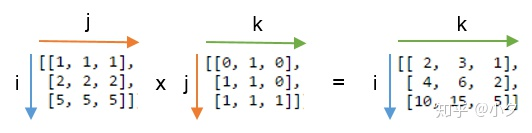
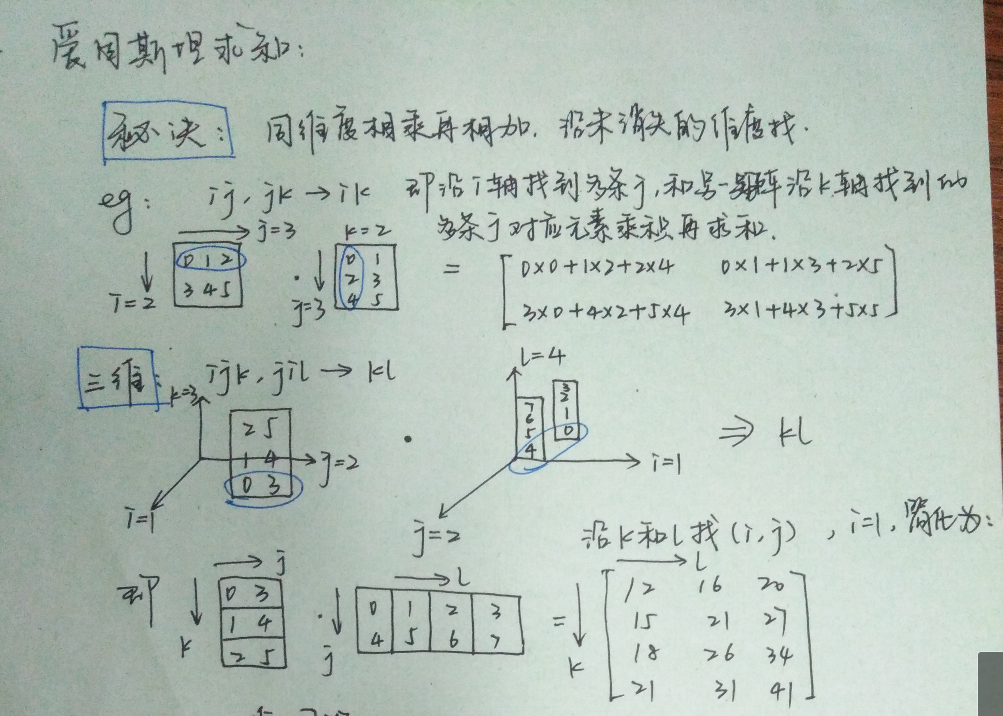
np.einsum('ij,jk->ijk', A, B)，注意此时的输出是三维的ijk，根据下图推测出计算方式是：用第一个矩阵i维度上的三个向量，即j向量，分别乘第二个矩阵沿着j方向的整个矩阵。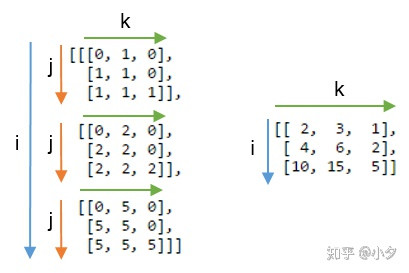
AB均是向量

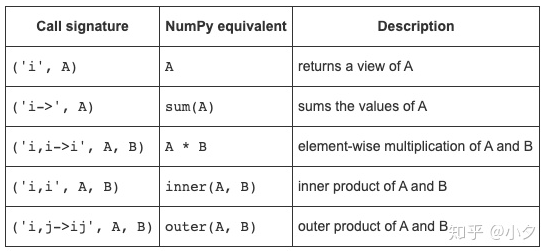
AB均是矩阵

我自己的理解

A = np.arange(18).reshape(3,2,3)
B = np.arange(24).reshape(2,3,4)

x = np.einsum('ijk,jil->kl',A,B)
print(A,'n',B,'n',x)
"""
[[[ 0  1  2]
  [ 3  4  5]]

 [[ 6  7  8]
  [ 9 10 11]]

 [[12 13 14]
  [15 16 17]]] 
 [[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]

 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]] 
 [[600 645 690 735]
 [660 711 762 813]
 [720 777 834 891]]
"""
# 第一个600的计算方法：12*3+16*9+4*6+12*8+15*20

还不明白的话，看我下面的图帮助理解，我认为矩阵问题，特别是高维tensor问题，一定要形象的画出来才方便理解。
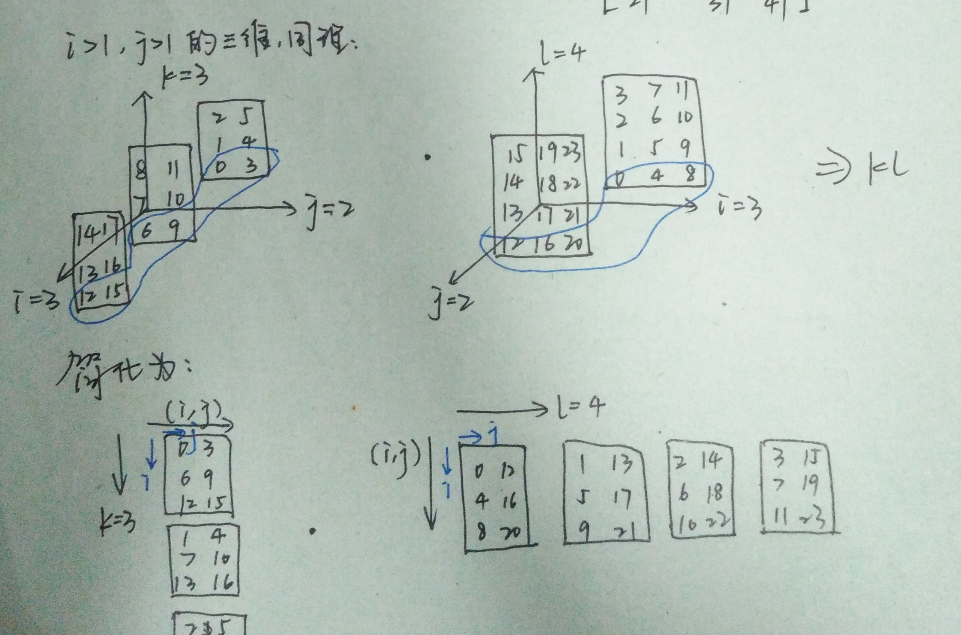
在这里插入图片描述
下面是一个代码中的具体例子：

torch.manual_seed(1)
x = torch.randn(1, 2, 3,4)
A = torch.randn(3, 2)
print(x,'n',A.T)
"""
tensor([[[[-1.5256, -0.7502, -0.6540, -1.6095],
          [-0.1002, -0.6092, -0.9798, -1.6091],
          [ 0.4391,  1.1712,  1.7674, -0.0954]],

         [[ 0.1394, -1.5785, -0.3206, -0.2993],
          [-0.7984,  0.3357,  0.2753,  1.7163],
          [-0.0561,  0.9107, -1.3924,  2.6891]]]]) 
 tensor([[ 3.5870,  1.5987,  0.3255],
        [-1.8313, -1.2770, -0.4791]])
"""
x = torch.einsum('ncvl,vw->ncwl', x, A)
# x.contiguous()
>>> x
"""
tensor([[[[-5.4895, -3.2838, -3.3369, -8.3767],
          [ 2.7113,  1.5907,  1.6020,  5.0480]],

         [[-0.7948, -4.8289, -1.1631,  2.5454],
          [ 0.7913,  2.0256,  0.9027, -2.9320]]]])
"""
# 据验证：sum(A.T[0]*x[0][0][:,1]) = tensor(-3.2838)