Hello,大家好，我是Tony

欢迎大家访问我的个人主页：Tony’s Blog，让我们一起站在巨人的肩膀之上！

神经网络的计算过程对应课程中9.1-9.8

神经网络的计算过程

对于二元分类问题（逻辑回归），系统输出的结果是1或0

对于多元分类问题，神经网络输出的结果是多维向量：
$$\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 1\\ 0\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 0\\ 1\\ 0\end{array}\right],\left[\begin{array}{l}0\\ 0\\ 0\\ 1\end{array}\right]$$
因此可以类比逻辑回归的代价函数来写出神经网络的代价函数：

一、一些要点

1.逻辑回归的代价函数（加正则化）：

$$J(\theta )=-\frac{1}{m}\left[\sum _{i=1}^m{y}^{(i)}\log h_{\theta }\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)\right]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$

对于逻辑回归、代价函数、代价函数正则化可以查看这篇博客：逻辑回归模型及代价函数正则化

对于机器学习中为什么要正则化可以查看这篇博客：机器学习中对过拟合的正则化策略

2、神经网络的代价函数

$$\begin{array}{rl}J(\Theta )=& -\frac{1}{m}\left[\sum _{i=1}^m\sum _{k=1}^K{y}_k^{(i)}\log {\left(h_{\Theta }\left(x^{(i)}\right)\right)}_k+\left(1-y_k^{(i)}\right)\log \left(1-{\left(h_{\Theta }\left(x^{(i)}\right)\right)}_k\right)\right]\\ & +\frac{\lambda }{2m}\sum _{l=1}^{L-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{l+1}}{\left({\Theta }_{ji}^{(l)}\right)}^2\end{array}$$

从上式可以看出 ，这相当于多个逻辑回归代价函数相加

3、反向传播算法（Back Propagation Algorithm）

利用反向传播算法计算DVec

4、梯度检测(Gradient Checking)

在进行梯度下降之后，要进行梯度检测，以保证梯度下降的正确性

for i=1:n
thetaPlus=theta;
thetaPlus(i)=thetaPlus(i)+EPSILON;
thetaMinus=theta;
thetaMinus(i)=thetaMinus(i)-EPSILON;
gradApprox(i)=（J(thetaPlus)-J(thetaMinus))/（2*EPSILON）；
end

Check gradApprox≈DVex?（from backpop），就是看这样求出的导数是否接近反向传播算法的值

5 神经网络的计算过程theta值初始化

$$(-ϵ\le {\Theta }_{ij}^{(l)}\le ϵ)$$

把theta值控制在[-E,E]之间

Theta1=rand(10,11)*(2*INIT_EPSILON-INIT_EPSILON;
Theta2=rand(1,11)*(2*INIT_EPSILON-INIT_EPSILON;

二、神经网络实现过程

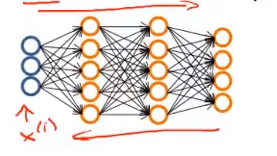
• 随机初始化权重接近0的值

• 前向传播算法计算
  $$h_{\Theta }\left(x^{(i)}\right)$$

• 计算代价函数J(θ)

• 反向传播算法计算局部偏导数
  $$\frac{\partial }{\partial {\Theta }_{jk}^{(l)}}J(\Theta )$$

• 梯度检测

• 梯度下降或其他高级算法来最小化代价函 数

重点：

确保 在迭代代码中不含梯度检测的代码，因为梯度检测速度比反向传播算法相比很慢，

最后

以上就是忧心网络为你收集整理的神经网络的计算过程神经网络的计算过程的全部内容，希望文章能够帮你解决神经网络的计算过程神经网络的计算过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。