支持向量机SVM(1)-线性可分支持向量机

线性可分支持向量机

本文包括以下部分

• 1.支持向量机概述
• 2.线性可分支持向量机与硬间隔最大化
  - (2.1)基本定义
  - (2.2)函数间隔与几何间隔的关系
  - (2.3) 硬间隔最大化
  - (2.4) 支持向量和间隔边界
• 3. 对偶算法

1.支持向量机概述

支持向量机是一种二类分类模型.它的基本模型是定义在特征空间上的间隔最大的线性分类器。其学习策略是间隔最大化，可形式化为求解凸二次规划问题，也等价于正则化的合叶损失函数的最小化问题。
支持向量机学习方法包含构建由简至繁的模型，可分为线性可分支持向量机、线性支持向量机、非线性支持向量机。

• 线性可分支持向量机：当训练数据线性可分时，通过硬间隔最大化，学习一个线性的分类器，又称为硬间隔支持向量机.
• 线性支持向量机：当训练数据近似线性可分时，通过软间隔最大化，也学习一个线性分类器，称为软间隔支持向量机.
• 非线性支持向量机：当训练数据不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机.

当输入空间为欧氏空间或离散集合，特征空间为希尔伯特空间时，核函数表示将输入从输入空间映射得到特征空间之间的内积，通过使用核函数可以学习非线性支持向量机，等价于隐式地在高维的特征空间中学习线性支持向量机，这样的方法称为核技巧。核方法是比支持向量机更为一般的机器学习方法。
本文按照上式思路首先记录线性可分支持向量机

2.线性可分支持向量机与硬间隔最大化

(2.1)基本定义
输入都由输入空间转换到特征空间，支持向量机的学习是在特征空间进行的。
假设给第一个特征空间上的训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯   , ( x N , y N ) } T=left{left(x_{1}, y_{1}right),left(x_{2}, y_{2}right), cdots,left(x_{N}, y_{N}right)right} T={(x1​,y1​),(x2​,y2​),⋯,(xN​,yN​)}其中 x i ∈ X = R n , y i ∈ Y = { + 1 , − 1 } , i = 1 , 2 , ⋯   , N x_{i} in mathcal{X}=mathbf{R}^{n}, quad y_{i} in mathcal{Y}={+1,-1}, quad i=1,2, cdots, N xi​∈X=Rn,yi​∈Y={+1,−1},i=1,2,⋯,N, $x_i$为第$i$个特征向量，也称为实例，$y_i$为$x_i$的类标记，当$y_i=+1$时，称$x_i$为正例；当时$y_i=-1$，称$x_i$为负例，$(x_i,y_i)$称为样本点.再假设训练数据集是线性可分的.
定义1（线性可分支持向量机）给定线性可分训练数据集，通过间隔最大化或等价地求解相应的凸二次规划问题学习得到分离超平面为
$$w^{\ast }\cdot x+b^{\ast }=0(1)$$以及相应的分类决策函数$$f(x)=\mathrm{sign}\left(w^{\ast }\cdot x+b^{\ast }\right)(2)$$称为线性可分支持向量机
定义2 (函数间隔) 对于给定的训练数据集$T$和超平面$(w,b)$,定义超平面$(w,b)$关于样本点$(x_i,y_i)$的函数间隔为$${\hat{\gamma }}_i=y_i\left(w\cdot x_i+b\right)(3)$$ 定义超平面$(w,b)$关于训练数据集$T$的函数间隔为超平面$(w,b)$关于中所有样本点$(x_i,y_i)$的函数间隔之最小值，即$$\hat{\gamma }=\underset{i=1,\cdots ,N}{\min }{\hat{\gamma }}_i(4)$$定义3 (几何间隔) 对于给定的训练数据集$T$和超平面$(w,b)$,定义超平面$(w,b)$关于样本点$(x_i,y_i)$的几何间隔为
$${\gamma }_i=y_i\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)(5)$$定义超平面$(w,b)$关于训练数据集$T$的函数间隔为超平面$(w,b)$关于中所有样本点$(x_i,y_i)$的几何间隔之最小值，即$$\gamma =\underset{i=1,\cdots ,N}{\min }{\gamma }_i(6)$$下图为函数间隔与几何间隔示例:

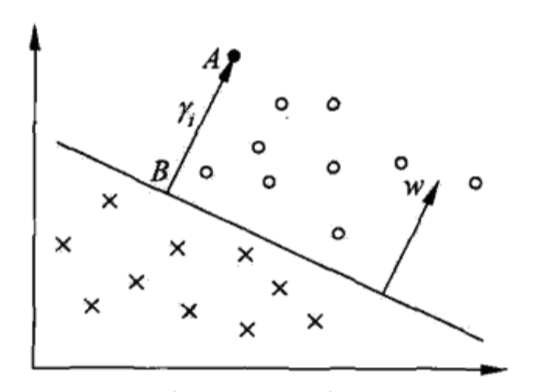
上图给出了超平面$(w,b)$及其法向量$w$，点$A$表示某一实例$x_i$,其类标记$y_i=+1$，点$A$与超平面$(w,b)$的距离由线段$AB$给出，记作${\gamma }_i$,
$${\gamma }_i=\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }$$其中，$\Vert w\Vert$为$w$的$L_2$范数，这是点$A$在超平面正的一侧的情形，若点$A$在超平面负的一侧，那么有$${\gamma }_i=-\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)$$当样本点$(x_i,y_i)$被超平面$(w,b)$正确分类时，点$x_i$与超平面$(w,b)$的距离是$${\gamma }_i=y_i\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)$$

(2.2)函数间隔与几何间隔的关系

$${\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert w\Vert }(7)$$$$\gamma =\frac{\hat{\gamma }}{\Vert w\Vert }(8)$$如果$\Vert w\Vert =1$，那么函数间隔和几何间隔相等，如果超平面参数和成比例地改变(超平面没有改变)，函数间隔也成比例改变，而几何间隔不变。实际上函数间隔${\hat{\gamma }}_i=y_i\left(w\cdot x_i+b\right)=y_i{f}_i(x)$ 就是$|f(x)|$,只是人为定义的一个间隔度量；而几何间隔${\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert w\Vert }=\frac{|f_i(x)|}{\Vert w\Vert }$才是直观上的点到超平面的距离.
点到平面距离公式：
$d=\left|\frac{A{x}_0+B{y}_0+C{z}_0+D}{\sqrt{A^2+B^2+C^2}}\right|$
其中$(x_0,y_0,z_0)$为空间中一点,$Ax+By+Cz+D=0$为平面方程，$d$为点到平面的距离.

(2.3) 间隔最大化

假设将$w$和$b$按比例改变为$\lambda a$和$\lambda b$，这时函数间隔为$\lambda \hat{\gamma }$,在超平面没有改变的情况下，函数间隔$\hat{\gamma }$可以任意大，因此函数间隔并不适合用来最大化一个量.几何间隔$\gamma =\frac{\hat{\gamma }}{\Vert w\Vert }$就不会出现这样的问题.
支持向量机的基本思想是求解能够正确划分数据集和几何间隔最大的分离超平面.
间隔最大化：对数据集找个几何间隔最大化意味着以充分大的确信度对训练数据进行分类.我们希望最大化超平面$(w,b)$关于训练数据集的几何间隔$\gamma$，约束条件表示的是超平面$(w,b)$关于每个训练样本点的几何间隔至少是$\gamma$.
问题可以表示为下面的约束最优化问题：
$$\underset{w,b}{\max }\gamma (9)$$$$\text{ s.t. }{y}_i\left(\frac{w}{\Vert w\Vert }\cdot x_i+\frac{b}{\Vert w\Vert }\right)⩾\gamma ,i=1,2,\cdots ,N(10)$$ 由几何间隔和函数间隔的关系$\gamma =\frac{\hat{\gamma }}{\Vert w\Vert }$，问题可以改写为$$\underset{w,b}{\max }\frac{\hat{\gamma }}{\Vert w\Vert }(11)$$$$\text{ s.t. }{y}_i\left(w\cdot x_i+b\right)⩾\hat{\gamma },i=1,2,\cdots ,N(12)$$函数间隔$\hat{\gamma }$的取值并不影响最优化问题的解。
假设将$w$和$b$按比例改变为$\lambda a$和$\lambda b$，这时函数间隔为$\lambda \hat{\gamma }$,而函数间隔的改变对最优化问题的不等式约束无影响，对目标函数的优化也没有影响，这样就可以取$\hat{\gamma }=1$,将$\hat{\gamma }=1$带入上面的优化问题$(11)$,由于最大化$\frac{1}{\Vert w\Vert }$和最小化$\frac{1}{2}\Vert w{\Vert }^2$是等价的，因此可得到下面的最优化问题
$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2(13)$$$$\text{ s.t. }{y}_i\left(w\cdot x_i+b\right)-1⩾0,i=1,2,\cdots ,N(14)$$这是一个凸二次规划问题.
凸优化问题是指约束最优化问题
$$\underset{w}{\min }f(w)(15)$$$$\text{ s.t. }{g}_i(w)⩽0,i=1,2,\cdots ,k(16)$$$$h_i(w)=0,i=1,2,\cdots ,l(17)$$其中，目标函数$f(w)$和约束函数$g_i(w)$都是$R^n$上的连续可微的凸函数，约束函数$h_i(w)$是$R^n$上的仿射函数，当目标函数$f(w)$是二次函数且约束函数$g_i(w)$是仿射函数是，上述凸最优化问题称为凸二次规划问题.
最大间隔分离超平面的存在唯一性
定理1(最大间隔分离超平面的存在唯一性) 若训练数据集线性可分，则将训练数据集中的样本点完全正确分开的最大间隔分离超平面存在且唯一.
证明:(1)存在性 (2)唯一性

(2.4) 支持向量和间隔边界

在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点点实例称为支持向量,支持向量是使约束条件式等号成立的点，即$y_i\left(w\cdot x_i+b\right)-1=0$.

• 对$y_i=+1$的正例点，支持向量在超平面$H_1:w\cdot x+b=1$上
• 对$y_i=-1$的负例点，支持向量在超平面$H_2:w\cdot x+b=-1$上

注意到$H_1$和$H_2$平行，在$H_1$和$H_2$之间形成一条长带，分离超平面与它们平行且位于它们中央，即$H_1$和$H_2$之间的距离成为间隔，间隔依赖于分离超平面的法向量$w$，等于$\frac{2}{\Vert w\Vert }$，$H_1$和$H_2$称为间隔边界.
在决定分离超平面时只有支持向量起作用，而其他实例点并不起作用。支持向量在确定分离超平面起着决定性作用，所以将这种分类模型称为支持向量机。支持向量的个数一般很少，所以支持向量机由很少的重要的训练样本确定。

3. 对偶算法

通过求解对偶问题得到原始问题的最优解，这就是线性可分支持向量机的对偶算法，其优点，一是对偶问题更容易求解. 二是自然引入核函数，进而推广到非线性分离问题$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2$$$$\text{ s.t. }{y}_i\left(w\cdot x_i+b\right)-1⩾0,i=1,2,\cdots ,N$$对上述不等式约束$(14)$引进拉格朗日乘子${\alpha }_i⩾0,i=1,2,\cdots ,N$，定义拉格朗日数：$$L(w,b,\alpha )=\frac{1}{2}\Vert w{\Vert }^2-\sum _{i=1}^N{\alpha }_i{y}_i\left(w\cdot x_i+b\right)+\sum _{i=1}^N{\alpha }_i(18)$$根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：
$$\underset{\alpha }{\max }\underset{w,b}{\min }L(w,b,\alpha )$$所以，为得到对偶问题的解，需要先求$L(w,b,\alpha )$对$w,b$的极小，再求对$\alpha$的极大.
1)求${\min }_{w,b}L(w,b,\alpha )$， 将拉格朗日函数分别对$w,b$求偏导数并令其等于0
$${\nabla }_{w}L(w,b,\alpha )=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0$$$${\nabla }_{b}L(w,b,\alpha )=\sum _{i=1}^N{\alpha }_i{y}_i=0$$得$$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$将上两式$(19)$带入$(18)$，并利用$(20)$即得
$$L(w,b,\alpha )=\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i{y}_i\left(\left(\sum _{j=1}^N{\alpha }_j{y}_j{x}_j\right)\cdot x_i+b\right)+\sum _{i=1}^N{\alpha }_i$$$$=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i$$即$$\underset{w,b}{\min }L(w,b,\alpha )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i$$

2) 求${\min }_{w,b}L(w,b,\alpha )$对$\alpha$的极大，即是对偶问题
$$\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)+\sum _{i=1}^N{\alpha }_i$$$$\text{ s.t. }\sum _{i=1}^N{\alpha }_i{y}_i=0$$$${\alpha }_i⩾0,i=1,2,\cdots ,N$$上式等价为$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\left(x_i\cdot x_j\right)-\sum _{i=1}^N{\alpha }_i$$$$\text{ s.t. }\sum _{i=1}^N{\alpha }_i{y}_i=0$$
原始问题满足《拉格朗日对偶性》中定理2的条件，所以存在$w^{\ast },{\alpha }^{\ast },{\beta }^{\ast }$，使$w^{\ast }$是原始问题的解,${\alpha }^{\ast },{\beta }^{\ast }$是对偶问题的解，因此原始问题可以转换为对偶问题求解。对线性可分训练数据集，假设对偶优化问题对$\alpha$的解为${\alpha }^{\ast }={\left({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }\right)}^{\mathrm{T}}$，可以由${\alpha }^{\ast }$求得原始优化问题对$(w,b)$的解$w^{\ast },b^{\ast }$.有下面定理
定理2 设${\alpha }^{\ast }={\left({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }\right)}^{\mathrm{T}}$是对偶最优化问题$(22)\sim (24)$的解，则寻在下标$j$，使得${\alpha }_j^{\ast }>0$，并可按下是求的原始优化问题$(13)\sim (14)$的解$w^{\ast },b^{\ast }$：$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i(25)$$$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x_j\right)(26)$$证明：根据《拉格朗日对偶性》定理3，KKT条件成立，即得
$${\nabla }_{w}L\left(w^{\ast },b^{\ast },{\alpha }^{\ast }\right)=w^{\ast }-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i=0$$$${\nabla }_{b}L\left(w^{\ast },b^{\ast },{\alpha }^{\ast }\right)=-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i=0$$$${\alpha }_i^{\ast }\left(y_i\left(w^{\ast }\cdot x_i+b^{\ast }\right)-1\right)=0,i=1,2,\cdots ,N$$$$y_i\left(w^{\ast }\cdot x_i+b^{\ast }\right)-1⩾0,i=1,2,\cdots ,N$$$${\alpha }_i^{\ast }⩾0,i=1,2,\cdots ,N$$由此得$w^{\ast }={\sum }_i{\alpha }_i^{\ast }{y}_i{x}_i$
其中至少有一个${\alpha }_j^{\ast }>0$（反证法，假设${\alpha }^{\ast }=0$，可知$w^{\ast }=0$，而$w^{\ast }=0$不是约束最优化问题的解，产生矛盾），因此对$j$有，$$y_j\left(w^{\ast }\cdot x_j+b^{\ast }\right)-1=0(28)$$将$(25)$带入$(28)$并注意到$y_j^2=1$，即得$b^{\ast }=y_j-{\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x_j\right)$由此定理，分离超平面可以写成$$\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x\cdot x_i\right)+b^{\ast }=0(29)$$分类决策函数可以写成$$f(x)=\mathrm{sign}\left(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x\cdot x_i\right)+b^{\ast }\right)(30)$$

参考：李航 《统计学习方法》
July 《支持向量机通俗导论 ——理解SVM的三层境界》
https://blog.csdn.net/v_july_v/article/details/7624837

最后

以上就是顺利面包最近收集整理的关于支持向量机SVM(1)-线性可分支持向量机的全部内容，更多相关支持向量机SVM(1)-线性可分支持向量机内容请搜索靠谱客的其他文章。