机器学习西瓜书第三章学习笔记-线性模型（线性回归、对数几率回归、LDA）

线性回归:解决回归问题，输出为连续的值

1. 数据集D = {(x1, y1), (x2, y2), … (xm, ym)}, 其中 xi 有d个属性描述， 多元线性回归试图学习一个线性模型以尽可能准确的预测实值输出标记。
   $f(x_i)=w^T{x}_i+b$ 使得 $f(x_i)\simeq y_i$

2. 可以利用最小二乘来对 w 和 b 进行估计，把 w 和 b 表示为向量形式 $\stackrel{⌢}{w}$ = ( w,b)，相应地， 把数据集D表示为一个m x (d+1) 维度的矩阵X, 其中每行的前 d 个元素对应于示例的 d 个属性值，最后一个元素恒为1，即如下，矩阵求导运算可以参考这里：
   
   

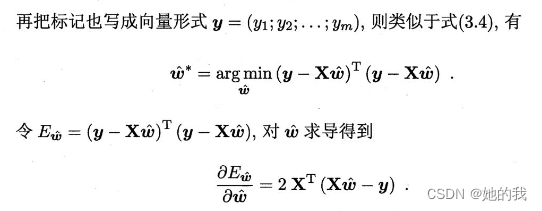
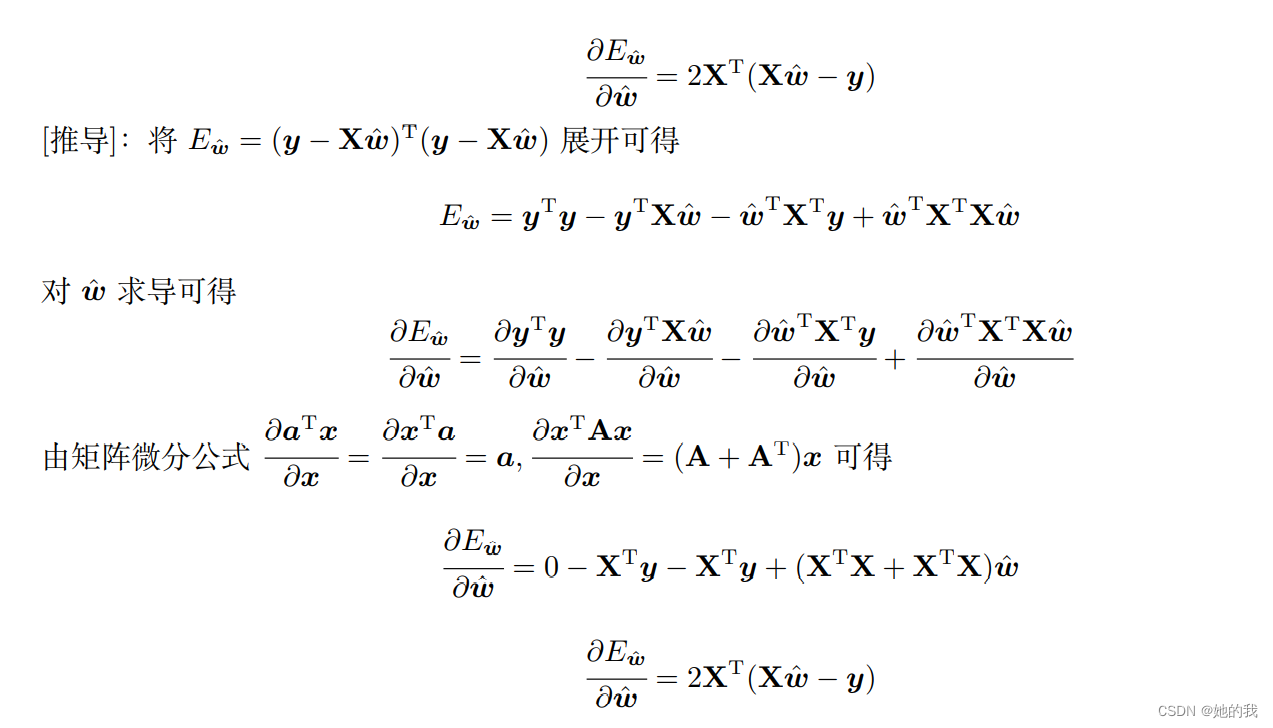
3. 当$X^{T}X$ 为满秩矩阵或正定矩阵（确定$X^{T}X$ 可逆的条件）令上述导数为0，可以求得 $\stackrel{⌢}{w\ast }=(X^{T}X{)}^{-1}{X}^{T}y$ , 进而得到线性模型。然而，现实情况下，$X^{T}X$ 不一定满秩， X 的列数大于行数，此时可以引入正则化，根据学习算法的归纳偏好选择合适的输出。

4. 可以令模型的预测值逼近y的衍生物， 假设我们认为示例所对应的输出标记是在指数上变化的， 那就可以将输出标记的对数作为线性模型逼近的目标，如：$\ln y=w^{T}x+b$ ,这就是对数线性回归，实质上是求输入空间到输出空间的非线性函数映射。更一般的可以考虑单调可微函数g(), 使得$y=g^{-1}{w}^{T}x+b$，这样得到的模型称为广义线性模型。
   

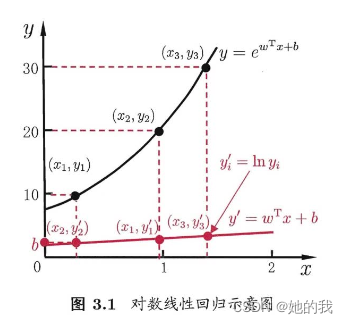
对数几率回归（logistic regression）：解决分类问题，输出离散的值

1. 考虑分类问题，将上述线性模型输出的连续的值转化为 0/1 值， 可以采用Sigmoid 函数。$y=\frac{1}{1+e^{-(w^{T}x+b)}}$, 进而推导得：$\ln \frac{y}{1-y}=w^{T}x+b$ （3.18式）, 其中 y 为x 为正例的可能性， 1-y 为负例的可能性， 即 w^Tx +b 线性模型学习到的是正例的相对可能性， 因此，此时需要用优化算法求得最优解， 确定此时的 w 和 b 。
   
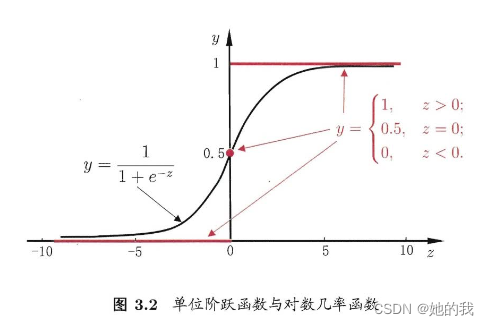
2. 用极大似然法，求解参数 w 和 b 。
   
   
   

线性判别分析（LDA）

参考 LDA

多分类问题

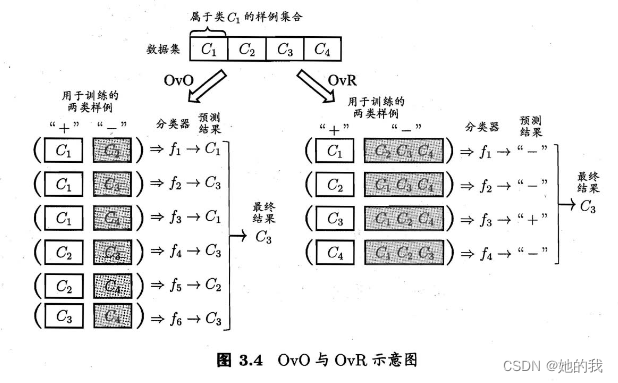
通常将多分类问题进行拆分，最经典的策略有：“一对一（OvO）”、“一对多余（OvR）”、“多对多（MvM）”.

1. OvO将N个类别两两配对， 从而产生$N(N-1)/2$个任务,在测试阶段，将新样本送给所有的分类器， 得到$N(N-1)/2$个结果，最终与预测的最多的作为结果。
2. OvR则是将一个类的样例作为正例，其他类作为反例，来训练N个分类器， 在测试时，若仅有一个分类器预测正类，则为最终结果，若有多个分类器预测为正类，则需要考虑分类器的预测置信度。训练OvO每个分类器仅用到两个类的样例，而OvR每次都要用到所有样例，在类别比较多时，OvR开销比较大，多数情况下性能比较差不多。
   
3. MvM每次将若干例作为正例，若干例作为反例，引入ECOC 纠错输出码。
   
   

类别不均衡问题

样本中不同类别样本数目差别很大，大体上由三类解决方法：欠采样(剔除多的)、过采样(补充少的)、阈值移动(基于原始数据集训练，预测时候做一次放缩)

最后

以上就是友好短靴为你收集整理的机器学习西瓜书第三章学习笔记-线性模型（线性回归、对数几率回归、LDA）的全部内容，希望文章能够帮你解决机器学习西瓜书第三章学习笔记-线性模型（线性回归、对数几率回归、LDA）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。