1. 首页
  2. 文章中心
  3. 机器学习

机器学习面试题特征工程模型评估降维无监督学习优化算法

113 阅读 0 评论
我是靠谱客的博主 无情大叔，最近开发中收集的这篇文章主要介绍机器学习面试题特征工程模型评估降维无监督学习优化算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

特征工程

特征工程队原始数据进行一系列工程处理
原始数据通常分为二种：

  • 结构化数据：结构化数据可以看成一个关系数据库的表，对应列名清晰，包含数值，类型两种基本类型
  • 非结构化数据：包含文本、图像、音频、视频数据

1.对数值类型特征归一化作用

对数值类型的特征做归一化，可以将所有特征都统一到一个大致相同的数值区间内，便于对不同特征数据进行对比分析，最常用的方法有两种：
（1）线性函数归一化（min-max scaling）
将数据映射到[0,1]的范围
（2）零均值归一化（z-score normalization）
将数据映射到均值为0，标准差为1的分布上

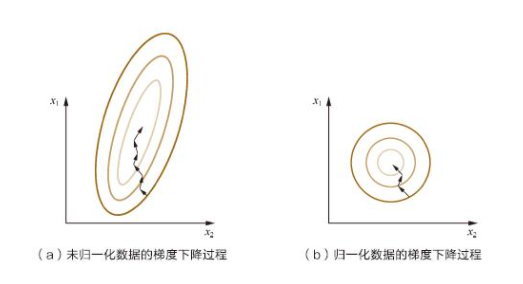
数据归一化对梯度下降收敛速度影响：
梯度下降

2.数据预处理，怎样处理类别型特征

通过对数据进行二次编码，具体方法有序号编码、独热编码、二进制编码。
（1）序号编码
序号编码通常处理类别间具有大小关系的数据，例如成绩可以分为优秀、良好、较差三档，序号编码会按大小关系对类别特征赋予数值ID，例如对优秀表示为3，良好为2，较差为1.
（2）独热编码
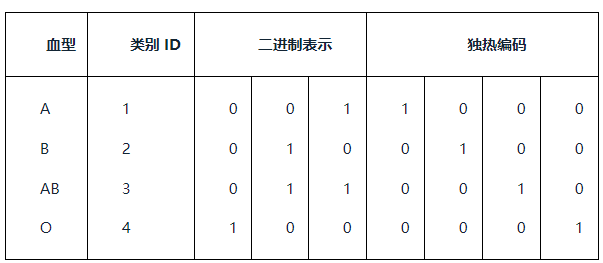
独热编码，处理类别间不具有大小关系的特征，例如血型，A型表示为（1,0，0,0），B型血表示为（0,1,0,0），AB型血表示为（0,0,1,0），O型血表示为（0,0,0,1），对于类别过多，可以使用稀疏向量搭建稀疏矩阵，并配合特征选择来降维。
（3）二进制编码
二进制编码

3.组合特征含义，怎样处理高维度组合特征

为了提高复杂关系的拟合能力，在特征工程中经常会把一阶离散特征两两组合，构成高阶组合特征
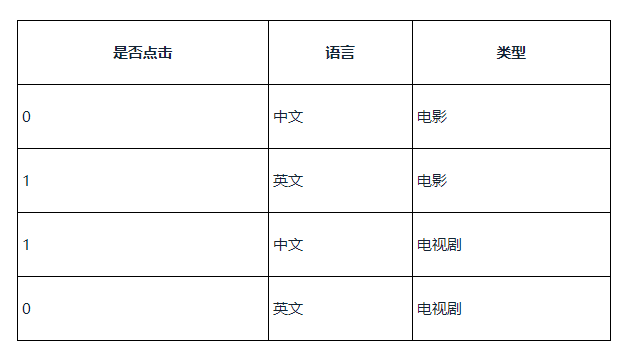
以广告点击预估问题为例：
下图为语言和类型对点击的影响
语言和类型对点击的影响
转化为组合特征：
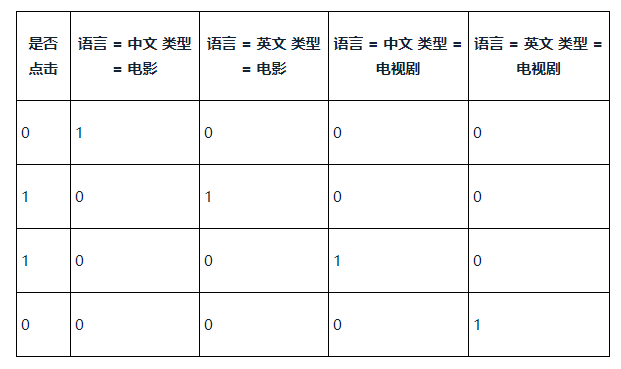
语言和类型的组合特征对点击影响
当遇到高维n维的情况，通常选择用低维向量表示。

4.有哪些文本表示模型，各有哪些优缺点

（1）词袋模型和N-gram模型
词袋模型将每篇文章的内容，以词为单位全部切分开，然后每篇文章可以用一些词表示为一个长向量，通过计算其词在原文章的权重反应该次的重要程度，常用TF-IDF计算
TF-IDF(t,d)=TF(t,d)xIDF(t)
其中TF(t,d)为单词t在文档d中出现的频率，IDF(t)是逆文档频率
IDF(t)=log(文章总数/包含单词t文章总数+1)
N-gram模型，对由几个词组成的单词，作为单独特征向量表示
（2）主题模型
（3）词嵌入与深度学习模型
word2vec，根据上下文各词预测当前词生成的概率，上下文词用独热编码表示，结合隐含层输入的权重矩阵，得到隐含层向量，再通过连接隐含层与输出层之间的权重矩阵，输出一个N向量，对输出层的向量应用Softmax激活函数，计算每个词的生成概率，Softmax激活函数定义为：
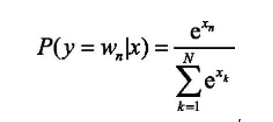
Softmax
LDA：是利用文档中单词的共现关系来对单词按主题聚类，通俗将就是通过对文档-单词矩阵，分解得到文档-主题和主题-单词两个概率分布

5.图像数据不足处理方法

背景：在做图像分类任务上，可能存在着训练数据不足的问题，导致模型存在过拟合方面，处理方法分为两类：
（1）基于模型，简化模型（非线性变为线性），添加正则约束项，集成学习，Droput参数
（2）基于数据，数据扩充，对原始数据进行适当的变换达到扩充数据集效果，具体方法比如：对图像随机旋转、平移、缩放、添加噪声扰动、颜色变换、改变图像亮度、对比度等

模型评估

模型评估一般分为离线评估与在线评估

1.评估指标的局限性

通常大部分评估指标只能片面的反映模型的一部分性能，存在指标的局限性。
（1）准确率局限性
准确率指分类正确的样本占总样本个数：
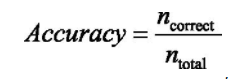
Accuracy
存在问题：如果样本中正样本占99%，分类器预测出为正样本准确率也为99%，这样对测试的样本预测，很可能出现问题，因为样本比例非常不均匀。
（2）精确率与召回率的权衡
精确率：分类正确的正样本个数占分类器判定位正样本个数
召回率：分类正确的正样本个数占真正正样本个数
精确率与召回率是互相矛盾的，以推荐系统为例，精确率越高推荐给用户的东西，符合用户喜好度越高，召回率越高，推荐给用户的东西，种类就越多，很可能还会出现一些冷门的东西。
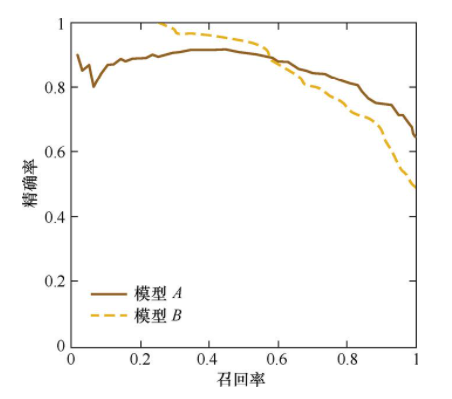
如何做到二个指标权衡，P-R曲线绘制，F1
P-R曲线

ROC曲线

（1）ROC曲线的横坐标为假阳性率(False Positive Rate，FPR)，纵坐标为真阳性率（True Positive TPR）
计算方法
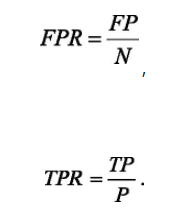
其中P是真实的正样本的数量，N是真实的负样本的数量，TP是P个正样本被分类器预测为正样本的个数，FP是N个负样本中被分类器预测为正样本个数
（2）AUC
AUC是指ROC曲线下的面积大小，该值量化反映基于ROC曲线衡量出模型的性能，计算AUC值只需要沿着ROC横轴做积分就可以了，AUC值越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。
（3）ROC与P-R曲线对比
当正负样本数量不均衡的时候，若选择不同测试集，P-R曲线变化就非常大，而ROC曲线则能够更稳定反映模型本身好坏。

余弦距离

选择余弦相似度和欧式距离的方法：
余弦相似度主要体现在方向上的相对差异，而欧式距离体现在数值上的绝对差异

A/B测试

（1）对模型进行充分离线评估之后，为什么还要进行在线A/B测试

  • 离线评估无法完全消除模型过拟合的影响
  • 离线评估无法完全还原线上工程环境，如线上环境的延迟，数据丢失等
  • 线上系统的一些商业指标，是离线评估无法计算的，如用户点击率，留存时长等
    （2）划分AB
    划分实验组和对照组

模型评估的方法

在样本划分和模型验证的过程中，存在不同的抽样方法和验证方法

  • Holdout检验
    将样本按照70%用于模型训练。30%用户模型验证
  • 交叉检验
    K-fold交叉验证，留一验证
  • 自助法
    针对样本规模比较小时，将样本集进行划分，对总数为N的样本集合，进行n次有放回随机抽样，得到大小为n的训练集

超参数调优

明确超参数搜索算法一般包括以下几点：
1.目标函数，即算法需要最大化/最小化的目标
2.搜索范围，一般通过上限和下限来确定
3.算法的其他参数

  • 网格搜索
  • 随机搜索
  • 贝叶斯优化

降维

如何定义主成分？从这种定义出发，如何设计目标函数使得降维达到提取主成分的目的？针对这个目标函数，如何对PCA问题进行求解？

求解方法：
（1）对样本数据进行中心化处理
（2）求样本协方差矩阵
（3）对协方差矩阵进行特征值分解，将特征值从大到小排列
（4）取特征值前d大对应的特征向量w1，w2…wd，通过以下映射将n维样本映射到d维

PCA求解是其实是最佳投影方向，即一条直线，以回归角度定义PCA的目标求解问题

从二维空间样本点来说，投影求解目的是得到一条直线，使得所有样本点投影到该直线的方差最大，其实从回归角度来说，也是求解一条直线使直线拟合这些样本。

对于一个高维空间，从回归角度，是希望找到一个d维的超平面，这个超平面到所有数据点之间的距离平方和最小。

线性判别LDA求解方式

线性判别是一种有监督学习算法，通常被用来对数据进行降维，相对PCA，PCA没有考虑到数据的类别，只是对原数据映射
LDA中心思想：最大化类间距离与最小化类内距离
求解方法：
（1）计算数据集中每个类别样本的均值向量uj，及总体均值向量u
（2）计算类内散度矩阵S（w）全局散度矩阵S（t），并得到类间散度矩阵S（b）=S（t）-S（w）
（3）对矩阵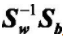矩阵进行特征值分解，对特征值排列
（4）取特征值前d大的对应特征向量，通过以下映射将n维样本映射到d维
映射
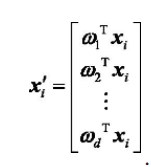
其中w为单位向量，D1，D2分别表示两类投影后的方差，对公式进行求导，求解最小值

PCA与LDA异同与区别联系

从求解过程：它们有很大的相似度，但对应原理有所不同
从目标过程：PCA选择投影后数据方差最大的方向，用主成分来表示原始数据可以去除的维度，达到降维，而LDA选择投影后类内方差小，类间方差大的方向。
从应用角度：对无监督的任务使用PCA，对监督的使用LDA

无监督学习

无监督学习主要包含两大类学习方法：数据聚类和特征变量关联

K均值聚类的优缺点，如何对其调优

k均值算法步骤（这里不做阐述）

  • 缺点：K均值受初始选择点和离散点的影响每次的结果不稳定，结果通常不是全局最优而是局部最优解，无法很好地解决数据簇分布差别比较大
  • 缺点：需要人工预先确定初始k，易受到噪点影响
  • 优点：对大数据集，k均值相对可伸缩和高效，它的计算复杂度接近于线性

调优

  • 数据归一化和离群点处理
  • 合理选择k值，尝试用使用不同k值，将k值对应的损失函数画成折线，横轴为k取值，纵轴为误差平方和所定义的损失函数
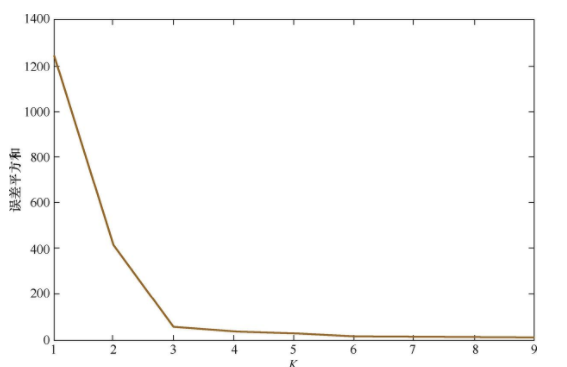
    k值与损失函数

改进模型

  • k-means++
    k-means++对初始值k值选择进行了改进
    原理：原始k均值算法是随机选取k个点作为聚类中心，而k-means++是假设已经选取了n个初始中心，则在选取第n+1个聚类中心，距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。
  • ISODATA算法，对初始值k值选择进行改进
    步骤有二种：
    （1）分裂操作，对应着增加聚类中心数
    （2）合并操作，对应着减少聚类中心数
    原理：预期设定聚类中心数目k，设定每个类最少要有的样本数目N（min），设置两个聚类中心之间允许的最小距离D（min），在选择初始k值进行聚类分类后，对分类后的样本进行检验，如果分类后样本包含的数目小于N（min），就不会对这个样本进行分类操作，如果分类后那个聚类中心之间的距离小于最小距离D（min），则合并这二个聚类的样本

证明k均值算法的收敛性

由于K均值聚类跌迭代算法实际上是一种最大期望算法，在这里先介绍EM算法

EM算法

原理：EM算法分两步，Expection-Step主要通过观察数据和现有模型来估计参数，然后利用这个参数计算似然函数的期望值，Maximization-Step寻找似然函数最大化时对应的参数
举例：
以抛硬币为例
https://zhuanlan.zhihu.com/p/78311644

优化算法

有监督学习的损失函数

损失函数

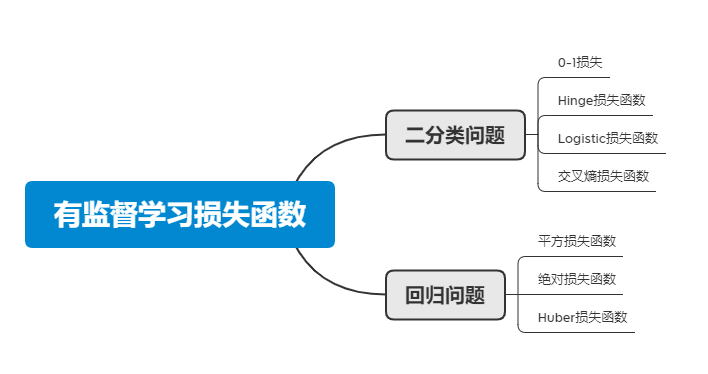
1.平方误差损失

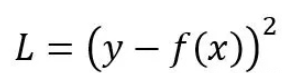
平方误差平均值
python实现更新权值

def update_weights_MSE(m,b,x,y,learning_rate):
    m_deriv=0
    b_deriv=0
    N=len(x)
    for i in range(N):
        #计算偏导数为
        # -2x(y - (mx + b))
        m_deriv += -2*x[i]*(y[i]-(m*x[i]+b))
        # -2(y - (mx + b))
        b_deriv += -2*(Y[i] - (m*X[i] + b))
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate 
    return m,b

2.绝对误差损失

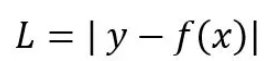
绝对误差损失
python实现更新权值

def update_weights_MAE(m,b,x,y,learning_rate):
    m_deriv=0
    b_deriv=0
    N=len(x)
    for i in range(N):
       #计算偏导数为
       # -x(y - (mx + b)) / |mx + b|
        m_deriv += - X[i] * (Y[i] - (m*X[i] + b)) / abs(Y[i] - (m*X[i] + b))
        # -(y - (mx + b)) / |mx + b|
        b_deriv += -(Y[i] - (m*X[i] + b)) / abs(Y[i] - (m*X[i] + b))
    #我们减去它，因为导数指向最陡的上升方向
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m, b

3.Huber损失

Huber损失结合了MSE和MAE的特性，对于误差较小时，它的损失函数是二次的，对于误差较大时，损失函数为线性。
Huber损失
python实现更新权值

def update_weights_Huber(m, b, X, Y, delta, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
        # 小值的二次导数，大值的线性导数
        if abs(Y[i] - m*X[i] - b) <= delta:
            m_deriv += -X[i] * (Y[i] - (m*X[i] + b))
            b_deriv += - (Y[i] - (m*X[i] + b))
        else:
            m_deriv += delta * X[i] * ((m*X[i] + b) - Y[i]) / abs((m*X[i] + b) - Y[i])
            b_deriv += delta * ((m*X[i] + b) - Y[i]) / abs((m*X[i] + b) - Y[i])
    #我们减去它，因为导数指向最陡的上升方向
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m, b

4.二元交叉熵损失

交叉熵损失函数原理：
交叉熵是信息论中一个重要概念，主要用于度量两个概率分布间的差异性，简单说就是用熵的和来做二元模型的损失函数

  • 信息熵
    信息熵称为熵，用来表示所有信息量的期望
    信息熵
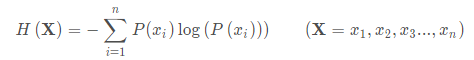
    对于0-1分布问题：
    0-1分布
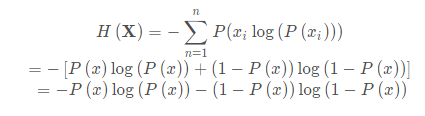
    概率分布P(x):
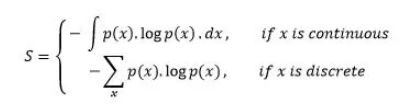
    二元交叉熵损失
    损失函数为：
    损失函数
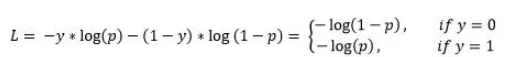
    python实现更新权值
def update_weights_BCE(m1,m2,b,x1,x2,y,learning_rate):
    m1_deriv=0
    m2_deriv=0
    b_deriv=0
    N=len(x1)
    for i in range(N):
        s=1/(1/(1+math.exp(-m1*x1[i]-m2*x2[i]-b)))
        #计算偏导数
        m1_deriv+=-x1[i]*(s-y[i])
        m2_deriv += -X2[i] * (s - Y[i])
        b_deriv += -(s - Y[i])
    # 我们减去它，因为导数指向最陡的上升方向
    m1 -= (m1_deriv / float(N)) * learning_rate
    m2 -= (m2_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m1, m2, b

5.Hinge损失

Hinge损失主要用于带有类标签-1和1的支持向量机（SVM），损失函数如下：
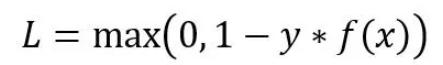
Hinge

def update_weights_Hinge(m1,m2,b,x1,x2,y,learning_rate):
    m1_deriv=0
    m2_deriv=0
    b_deriv=0
    N=len(x1)
    for i in range(N):
       if y[i]*(m1*x1[i]+m2*x2[i]+b)<=1:
          m1_deriv+=-x1[i]*y[i]
          m2_deriv+=-x2[i]*y[i]
          b_deriv+=-y[i]
    m1 -= (m1_deriv / float(N)) * learning_rate
    m2 -= (m2_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
return m1, m2, b

待更新…

最后

以上就是无情大叔为你收集整理的机器学习面试题特征工程模型评估降维无监督学习优化算法的全部内容，希望文章能够帮你解决机器学习面试题特征工程模型评估降维无监督学习优化算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(75)

相关文章

slam系统中部分位姿转换问题
slam系统中部分位姿转换问题
Python OpenCV实例：图像重映射
Python OpenCV实例：图像重映射
视觉十四讲:第十讲_位姿图
视觉十四讲:第十讲_位姿图
相机标定、相机位姿
相机标定、相机位姿
机器学习面试题特征工程模型评估降维无监督学习优化算法
机器学习面试题特征工程模型评估降维无监督学习优化算法
抠像技术介绍
抠像技术介绍
通俗易懂！视觉slam第六部分——旋转向量，欧拉角
通俗易懂！视觉slam第六部分——旋转向量，欧拉角
菜鸟专学：Eigen--Sophus--CV--三种不同库对矩阵的操作方式
菜鸟专学：Eigen--Sophus--CV--三种不同库对矩阵的操作方式

评论列表共有 0 条评论

立即
投稿
返回
顶部