动态规划-连续子数组的最大和-JZ30

描述
输入一个整型数组，数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为 O(n).

示例1

输入： [1,-2,3,10,-4,7,2,-5]
返回值： 18
说明：输入的数组为{1,-2,3,10,—4,7,2,一5}，和最大的子数组为{3,10,一4,7,2}，因此输出为该子数组的和 18。

思路

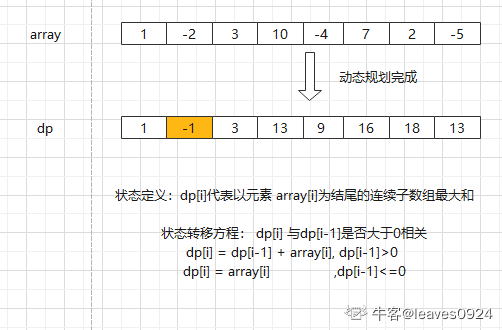
直接用简化动态规划，使用一个变量sum来表示当前连续的子数组和，以及一个变量res来表示中间出现的最大的和。
时间复杂度O(n)，空间复杂度O(1)
代码

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if (array == null || array.length == 0) {
            return 0;
        }
        //res表示所有子数组的和的最大值
        int res = array[0];
        //sum表示包含当前连续的子数组和
        int sum = array[0];
        for (int i = 1; i < array.length; ++i) {
            sum = max(sum + array[i], array[i]);
            res = max(res, sum);
        }
        return res;
    }
    private int max(int i, int j) {
        return i > j ? i : j;
    }
}

最后

以上就是清秀秋天为你收集整理的动态规划-连续子数组的最大和-JZ30的全部内容，希望文章能够帮你解决动态规划-连续子数组的最大和-JZ30所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。