我是靠谱客的博主 寒冷大白，最近开发中收集的这篇文章主要介绍基于四叉树的图像压缩问题一、综合训练目的与要求二、综合训练任务三、问题理解四、设计算法七、代码实现算法并测试八、分析算法的时间和空间复杂性，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
一、综合训练目的与要求
《程序设计与算法综合训练》是一门面向软件工程专业、网络工程专业、计算机科学与技术专业的综合实践课程。它是配合专业学科平台课程《高级语言程序设计》和《数据结构》而开设的实践性教育环节。
本课程的目的是：通过本课程的综合实践训练，使学生加深对《高级语言程序设计》和《数据结构》课程中基本知识与基本原理的理解；掌握各种数据类型的使用技巧和模块化程序设计的方法；掌握程序设计的过程和技巧，确立分析问题、建立模型和运用程序进行问题求解的思维方式；掌握复杂数据结构在计算机中的存储表示及其运算，建立正确的数据组织与数据处理的设计思想，培养学生综合运用数据结构课程的相关设计理论与实际问题相结合解决数据组织与分析、数据处理与算法设计等设计问题的能力。
二、综合训练任务
综合训练项目任务是在完成程序设计的同时能够写出比较规范的设计报告。严格实施综合训练项目这一环节，对于基本程序设计素养的培养和软件工作者工作作风的训练，将起到显著的促进作用。
三、问题理解
四叉树 (Quad Tree) 算法可以将大量坐标数据压缩保存，通常将给定空间分割为4个，然后以递归形式表示（此即四叉树的得名由来）。最著名的应用是对黑白图像的压缩。四叉树以字符串的形式对2^N × 2^N的黑白图像进行如下压缩：
- 若区域的图像的所有像素为黑色，则四叉树压缩的结果都是字符b（无论图像区域的大小是多少，哪怕是整幅图像）；
- 若区域的图像的所有像素为白色，则四叉树压缩的结果都是字符w（无论图像区域的大小是多少，哪怕是整幅图像）；
- 若区域图像的像素不同色，则先把图像区域纵向及横向各一分为二，然后对4个小图像区域进行四叉树压缩。而该区域图像的压缩结果字符串为x（左上部分的压缩结果）（右上部分的压缩结果）（左下部分的压缩结果）（右下部分的压缩结果）。
四、设计算法
- 算法策略
- 将输入的压缩图像放入单链表中
- 将压缩图像还原为图像
- 将图像上下翻转
- 将翻转后的图像转换为四叉树压缩图像
- 数据结构的选定
因为要输入多个压缩图像，所以将压缩图像放入单链表中，便于后续的查询，插入，删除，打印等基本操作。
- 算法思想
四叉树（Quad Tree）是一种空间索引树，四叉树的每一个节点都代表着一块矩形区域。我们知道在平面直角坐标系中，平面可以被分为第一二三四象限，四叉树的每一个节点也类似，可以分裂为四个子节点，子节点在满足条件的情况下可以继续分裂，这样构成了一个四元的树状结构，就是四叉树。
通常使用树结构能够带来高效且简单的检索效果，四叉树也不例外，四叉树主要用于二维空间的检索（相应的，三维空间可以了解下八叉树，理论上来讲，对于N维空间的检索可以根据这个原理构成2^N叉树，此外多维空间的检索还有kd树）。
其中这个区域被分为了许多个小矩形，每一个矩形都代表了一个四叉树的一个节点，最外层的大矩形就是四叉树的根节点（root），一些矩形被分割成了四个等大的小矩形，这是该节点的四个子节点，矩形越小，说明该节点的深度（depth）越大。
四叉树的操作
1、节点分裂
当满足特定条件时，为了获得更好的检索效率，四叉树的节点会发生分裂，分裂的做法是：以当前节点的矩形为中心， 划分出四个等大的矩形，作为四个子节点，每个节点深度=当前节点深度+1，根节点深度为0；并且将当前节点的元素重新插入到对应的子节点。
2、插入元素
1）平面的元素多种多样，点，线，图形，但都能够做一个统一，第一步都是要找出图形所覆盖的节点，这里以矩形为例
2）从根节点开始，如果当前节点无子节点，将元素插入到当前节点。如果存在子节点K，并且元素能够完全被子节K点所“包围”，就将元素插入到子节点K，对于子节点K进行上述递归操作；如果元素跨越了多个子节点，那就将元素存储在当前节点
3）如果某一节点元素超过特定值，并且深度小于四叉树允许的最大深度，分裂当前节点。
3、检索
1）对于给定检索区域，从根节点起，如果检索区域与当前节点有交集，返回当前节点的所有元素。
2）如果当前节点还有子节点，递归检索与检索区域有交集的子节点。
- 求解步骤
- 输入压缩图像个数，并以此输入每个压缩图像。
- 将输入的压缩图像字符串放入单链表中。
- 遍历单链表，将每一个字符串初始化为四叉树。
- 将四叉树压缩图像递归转化为原始图像。
- 将原始图像进行上下翻转。
- 将翻转之后的图像递归转化为压缩图像。
七、代码实现算法并测试
1. 代码实现
four_char.h
#pragma once
#include <iostream>
using namespace std;
#include <string>
#include "in_out.h"
#include <algorithm>
#include "List.h"
#include<math.h>
/*定义四叉树的结构*/
typedef struct Node
{
struct Node* super;
char data; /*数据域*/
struct Node* up_lchild, * up_rchild, * dw_lchild, * dw_rchild; /*四棵子树*/
int count;
} *FourTree, FourNode;
/*整棵树和结点名称*/
int Depth(FourTree T);
LineList<string> transport(LineList<string>& L);
string process(string s);
void CreateFourTree(FourTree& T, string& s, int& count, int& length);
void print_jz(char** arr, int hang);
void bianhuan(FourTree& T, char** arr, int x1, int x2, int y1, int y2, int changx, int changy);
char** daozhi(char** arr, int length);
string& check(char** arr, int x1, int x2, int y1, int y2, string& str, int& count, int length, int changx, int changy);
string bianhuan_2(char** arr, int hang, int head, int index, int length, string& str);
LineList<string> transport(LineList<string>& L) {
LinkNode<string>* current = L.first;
for (int i = 1; i <= L.length; i++) {
current = current->link;
string s = current->data;
current->data = process(s);
}
cout << endl;
return NULL;
}
/*创建四叉树*/
void CreateFourTree(FourTree& T, string& s, int& count, int& length)
{
if (count >= length) {
return;
}
char ch;
ch = s[count];
count++;
T = new FourNode; /*创建一个新节点*/
T->up_lchild = NULL;
T->up_rchild = NULL;
T->dw_lchild = NULL;
T->dw_rchild = NULL;
T->data = ch;
if (T->data == 'x') {
if (T->up_lchild == NULL) {
CreateFourTree(T->up_lchild, s, count, length);
}
if (T->up_rchild == NULL) {
CreateFourTree(T->up_rchild, s, count, length);
}
if (T->dw_lchild == NULL) {
CreateFourTree(T->dw_lchild, s, count, length);
}
if (T->dw_rchild == NULL) {
CreateFourTree(T->dw_rchild, s, count, length);
}
}
else {
return;
}
}
void print_jz(char** arr, int hang) {
for (int i = 0; i < hang; i++) {
for (int j = 0; j < hang; j++) {
cout << " " << arr[i][j];
}
cout << endl;
}
}
// 矩阵倒置
char** daozhi(char** arr, int length) {
char** n_jz = new char* [length];
for (int i = 0; i < length; i++) {
n_jz[i] = new char[length];
for (int j = 0; j < length; j++) {
n_jz[i][j] = '.';
}
}
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
n_jz[i][j] = arr[length - 1 - i][j];
}
}
delete arr;
return n_jz;
}
void bianhuan(FourTree& T, char** arr, int x1, int x2, int y1, int y2, int changx, int changy) {
if (T == NULL)
{
return;
}
if (T->data == 'x') {
if (T->up_lchild != NULL) {
int x11 = 0+changx;
int x22 = (int)(x2 - changx) / 2 + changx;
int y11 = 0+changy;
int y22 = (int)(y2 - changy) / 2 + changy;
bianhuan(T->up_lchild, arr, x11, x22, y11, y22, changx, changy);
}
if (T->up_rchild != NULL) {
int x11 = 0+changx;
int x22 = (int)(x2 - changx) / 2 + changx;
int y11 = (int)(y2-changy) / 2 + changy;
int y22 = y2;
int changY_1 = changy;
changY_1 += (int)((y2 - changy)/ 2);
bianhuan(T->up_rchild, arr, x11, x22, y11, y22, 0, changY_1);
}
if (T->dw_lchild != NULL) {
int x11 = (int)(x2 - changx) / 2 + changx;
int x22 = x2;
int y11 = 0+changy;
int y22 = (int)(y2 - changy) / 2 + changy;
int changX_1 = changx;
changX_1 += (int)((x2 - changx) / 2);
bianhuan(T->dw_lchild, arr, x11, x22, y11, y22, changX_1, 0);
}
if (T->dw_rchild != NULL) {
int x11 = (int)(x2 - changx) / 2 + changx;
int x22 = x2;
int y11 = (int)(y2 - changy) / 2 + changy;
int y22 = y2;
int changX_1 = changx;
changX_1 += (int)((x2 - changx) / 2);
int changY_1 = changy;
changY_1 += (int)((y2 - changy) / 2);
bianhuan(T->dw_rchild, arr, x11, x22, y11, y22, changX_1, changY_1);
}
}
else {
for (int i =x1; i < x2; i++) {
for (int j = y1; j < y2; j++) {
if (T->data == 'b') {
arr[i + 2][j + 2] = ' ';
}
else {
arr[i + 2][j + 2] = '#';
}
}
}
}
}
/*求树的深度*/
int Depth(FourTree T)
{
if (T == NULL)
return 0;
else
{
int i = Depth(T->up_lchild);
int j = Depth(T->up_rchild);
int k = Depth(T->dw_lchild);
int l = Depth(T->dw_rchild);
return max(max(i+1, j+1), max(k+1, l+1));
}
}
//=============================================================================================================
//=============================================================================================================
//=============================================================================================================
string& check(char** arr, int x1, int x2, int y1, int y2, string& str, int &count, int length, int changx, int changy) {
if (count >= length) {
return str;
}
char ch = '_';
ch = arr[x1+2][y1+2];
for (int i = x1; i < x2; i++) {
for (int j = y1; j < y2; j++) {
if (ch != arr[i+2][j+2]) {
str[count] = 'x';
count++;
int x11 = 0 + changx;
int x22 = (int)(x2 - changx) / 2 + changx;
int y11 = 0 + changy;
int y22 = (int)(y2 - changy) / 2 + changy;
check(arr, x11, x22, y11, y22, str, count, length,changx,changy);
x11 = 0 + changx;
x22 = (int)(x2 - changx) / 2 + changx;
y11 = (int)(y2 - changy) / 2 + changy;
y22 = y2;
int changY_1 = changy;
changY_1 += (int)((y2 - changy) / 2);
check(arr, x11, x22, y11, y22, str, count, length, 0, changY_1);
x11 = (int)(x2 - changx) / 2 + changx;
x22 = x2;
y11 = 0 + changy;
y22 = (int)(y2 - changy) / 2 + changy;
int changX_1 = changx;
changX_1 += (int)((x2 - changx) / 2);
check(arr, x11, x22, y11, y22, str, count, length, changX_1, 0);
x11 = (int)(x2 - changx) / 2 + changx;
x22 = x2;
y11 = (int)(y2 - changy) / 2 + changy;
y22 = y2;
changX_1 = changx;
changX_1 += (int)((x2 - changx) / 2);
changY_1 = changy;
changY_1 += (int)((y2 - changy) / 2);
check(arr, x11, x22, y11, y22, str, count, length, changX_1, changY_1);
return str;
}
}
}
if (ch == ' ') {
str[count] = 'b';
}
else {
str[count] = 'w';
}
count++;
return str;
}
string bianhuan_2(char** arr, int hang, int head, int index, int length, string& str) {
int x1 = head;
int x2 = index;
int y1 = head;
int y2 = index;
int count = 0;
check(arr, x1, x2, y1, y2, str, count, length,0,0);
return str;
}
string process(string s) {
int count = 0;
int length = s.length();
FourTree T;
CreateFourTree(T, s, count, length);
int hang = Depth(T);
cout << "=======================================" << endl;
cout << "=======================================" << endl;
cout << endl;
cout << endl;
cout << endl;
int index = sqrt(pow(4, hang - 1));
int hang2 = hang - 1;
hang = sqrt(pow(4, hang - 1)) + 4;
int head = 0;
char** jz = new char* [hang];
for (int i = 0; i < hang; i++) {
jz[i] = new char[hang];
for (int j = 0; j < hang; j++) {
jz[i][j] = '.';
}
}
int chang = 0;
bianhuan(T, jz, head, index, head, index, 0,0);
print_jz(jz, hang);
jz = daozhi(jz, hang);
cout << "=======================================" << endl;
print_jz(jz, hang);
string str = s;
string s2 = bianhuan_2(jz, hang2, head, index, length, str);
return s2;
}in_out.h
#include <iostream>
using namespace std;
#pragma once
#include <string>
#include "four_cha.h"
#include "List.h"
void input(LineList<string>* In) {
int n1;
cin >> n1;
LineList<string> L1(n1);
In->first = L1.first;
In->length = L1.length;
}
List.h
#pragma once
#include <iostream>
#include <string>
using namespace std;
template <class T>
struct LinkNode {
T data;
LinkNode<T>* link;
LinkNode() {
link = NULL;
}
LinkNode(const T& item) {
data = item;
link = NULL;
}
};
template <class T>
class LineList {
public:
int length;
LinkNode<T>* first;
public:
LineList() {}
LineList(int n) {
length = n;
first = new LinkNode<T>();
LinkNode<T>* current = first;
for (int i = 0; i < length; i++) {
T num;
cin >> num;
LinkNode<T>* newnode = new LinkNode<T>(num);
current->link = newnode;
current = newnode;
}
}
bool Insert(int x, int j) {
LinkNode<T>* newnode = new LinkNode<T>(x);
LinkNode<T>* current = first;
for (int i = 1; i <= length; i++) {
current = current->link;
if (i == j - 1) break;
}
newnode->link = current->link;
current->link = newnode;
length++;
return true;
}
bool Remove(int j) {
LinkNode<T>* current = first;
if (j == 1) {
current = current->link;
first->link = current->link;
delete current;
length--;
return true;
}
else {
for (int i = 1; i <= length; i++) {
current = current->link;
if (i == j - 1) break;
}
LinkNode<T>* current1 = current->link;
current->link = current->link->link;
delete current1;
length--;
return true;
}
return true;
}
bool Search(int x) {
LinkNode<T>* current = first;
for (int i = 1; i <= length; i++) {
current = current->link;
if (current->data == x) {
cout << i << endl;
return true;
}
}
cout << "Not found" << endl;
return false;
}
void NiZhi() {
LinkNode<T>* current = first;
LinkNode<T>* second = new LinkNode<T>();
LinkNode<T>* current2 = second;
int k = length;
for (int j = 1; j <= length; j++) {
for (int i = 1; i <= k; i++) {
current = current->link;
if (i == k) break;
}
current2->link = current;
current2 = current;
current = first;
k--;
}
first = second;
}
void Sort() {
LinkNode<T>* current = first;
LinkNode<T>* p;
LinkNode<T>* q;
for (p = current->link; p != NULL; p = p->link)
{
for (q = p->link; q != NULL; q = q->link) {
if (p->data > q->data)
{
int tmp = q->data;
q->data = p->data;
p->data = tmp;
}
}
}
}
void Print() {
LinkNode<T>* current = first;
for (int i = 1; i <= length; i++) {
current = current->link;
cout << current->data << endl;
}
cout << endl;
}
void HeBing(LineList<T>& L) {
LinkNode<T>* current = first;
for (int i = 1; i <= length; i++) {
current = current->link;
if (i == length) {
break;
}
}
current->link = L.first->link;
length += L.length;
}
};index.cpp
#include <iostream>
using namespace std;
#include "four_cha.h"
#include "in_out.h"
#include "List.h"
#include <string>
int main() {
LineList<string> In;
input(&In);
// 调用测试数据处理函数
cout << "开始执行" << endl;
transport(In);
cout << "输出结果：" << endl;
In.Print(); // 打印产生的测试数据
return 0;
}
2. 算法测试
输入：
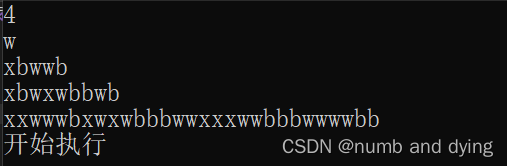
输出：
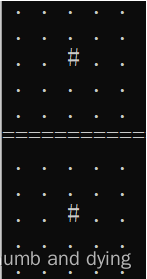
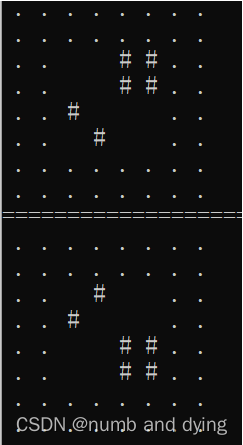
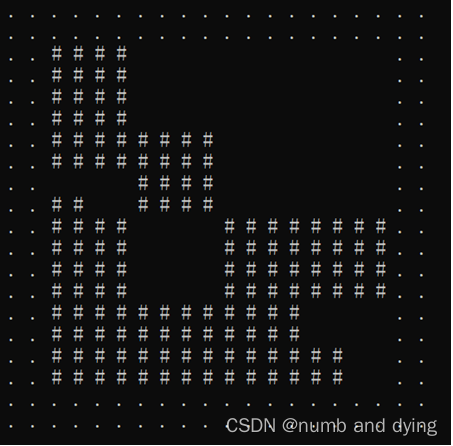
最终结果：
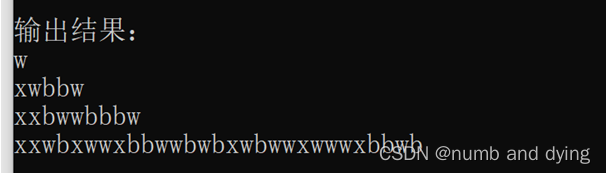
八、分析算法的时间和空间复杂性
- 时间复杂性
在程序刚开始运行时，输入k个字符串，每个字符串的长度为n，对字符串操作时，判断字符串每一个自符的值，如果为x，则继续调用该函数，如果不是，则将这个节点的值设为字符的值。因此四叉树插入时间复杂度最大为O(n)。若是四叉树比较平衡，其时间复杂度下降，最小的时间复杂度为O(logn)。
之后是将初始化为一个二维数组还原压缩图像，树的最大高度为n，所以时间复杂度最大为O(n^2)。之后根据四叉树给二维数组赋值，所以时间复杂度为O(n^2*logn)。之后将图像倒置，所用时间为O(n^2)，最后是将倒置的图像转换为压缩图像，转换的过程中，要对分块的二维数组遍历，所以时间的复杂度为O(n^2)。
综上所述，该算法的时间复杂度为O(n^2*logn)。
- 空间复杂性
在程序刚开始运行时，输入k个字符串，每个字符串的长度为n，所用空间为O(n)，之后创建四叉树，所用的空间为O(n)，然后是新建一个二维数组，所用的空间复杂度为O(n^2)，最后是将二维数组转换为四叉树压缩图像，所用空间为O(n)。
综上所述，该算法的空间复杂度为O(n^2)。
最后
以上就是寒冷大白为你收集整理的基于四叉树的图像压缩问题一、综合训练目的与要求二、综合训练任务三、问题理解四、设计算法七、代码实现算法并测试八、分析算法的时间和空间复杂性的全部内容，希望文章能够帮你解决基于四叉树的图像压缩问题一、综合训练目的与要求二、综合训练任务三、问题理解四、设计算法七、代码实现算法并测试八、分析算法的时间和空间复杂性所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复