完全背包问题

完全背包问题

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

状态转移：

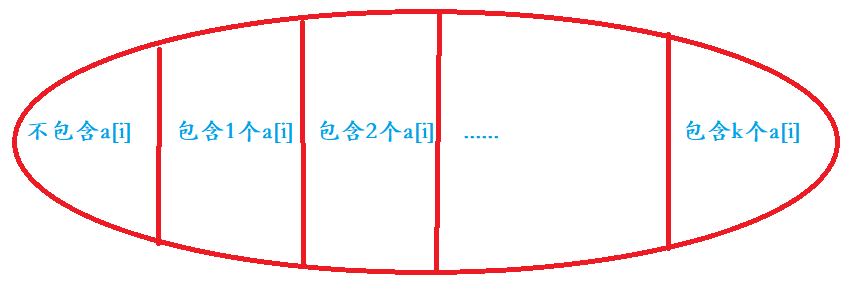
朴素做法：

#include <iostream>
using namespace std;
const int N = 1010;
int v[N],w[N];
int f[N][N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];
            for(int k=0;k*v[i]<=j;k++){
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<f[n][m];
    return 0;
}

优化做法：

f[i]表示总体积是i的情况下，最大价值

#include <iostream>
using namespace std;
const int N = 1010;
int f[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        int v,w;
        cin>>v>>w;
        for(int j=v;j<=m;j++)
            f[j]=max(f[j],f[j-v]+w);
    }
    cout<<f[m];
    return 0;
}

最后

以上就是沉默电灯胆为你收集整理的完全背包问题的全部内容，希望文章能够帮你解决完全背包问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。