手写一个归并序列，并对其改进，这样的面试题你还能手撕面试官吗手写一个归并序列，并对其改进，这样的面试题你还能手撕面试官吗

54 阅读 0 评论 36 点赞

我是靠谱客的博主冷酷跳跳糖，最近开发中收集的这篇文章主要介绍手写一个归并序列，并对其改进，这样的面试题你还能手撕面试官吗手写一个归并序列，并对其改进，这样的面试题你还能手撕面试官吗，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

手写一个归并序列，并对其改进，这样的面试题你还能手撕面试官吗

前言:

归并排序是利用归并的思想实现的排序算法，该算法采用经典的分治策略(分治法是将问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

基本思想：分的阶段就是递归拆分子序列的过程，治的阶段就是将俩个有序的子序列合并成一个有序的序列。

一、排序原理

归并排序的思想很简单，如果有一组待排序列，先切分再重组。任何一篇教程也都会说采用的是分治法，意思就是这么个意思，再细致一点的理解就是：

将一组待排序，先分割成一个一个的元素，然后将这些元素先两两排序，再四四排序，八八排序，一直到排序完所有的元素。

也就是说归并排序其实就是将已有序的子序列合并，得到完全有序的序列。我们看一张动图来认识一下：

是不是有点理解了，动态图的作用其实就是为了方便你了解整个归并过程，不理解也没关系，我们再来看一张静态图，帮助你从细节上来理解。

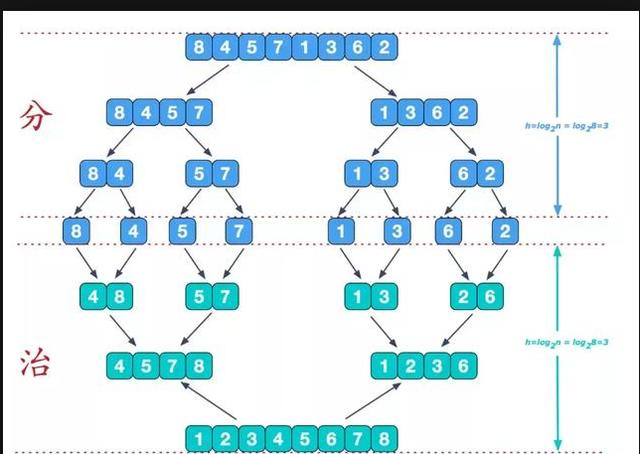
上面的这张图基本上能把整个归并排序的流程了解清楚了。也就是文章开头提到的先切分再重组。下面我们使用代码来实现一下归并排序，并对其做一个改进：

二、代码实现

1、基本实现

基本实现的思想很简单，我们就是先切分成一个个元素，然后再合并就好了。

//data：表示待排序列
//left：表示当前序列的左边界
//right：表示当前序列的右边界
public static void sort(int[] data, int left, int right) {
 if (left >= right)
 return;
 // 找出中间索引
 int center = (left + right) / 2;
 // 对左边数组进行递归
 sort(data, left, center);
 // 对右边数组进行递归
 sort(data, center + 1, right);
 // 合并
 merge(data, left, center, right);
 print(data);
}

然后我们看一下合并：

public static void merge(int[] data, int left, int center, int right) {
 int[] tmpArr = new int[data.length];
 int mid = center + 1;
 int third = left;
 int tmp = left;
 while (left <= center && mid <= right) {
 // 从两个数组中取出最小的放入临时数组
 if (data[left] <= data[mid]) {
 tmpArr[third++] = data[left++];
 } else {
 tmpArr[third++] = data[mid++];
 }
 }
 // 剩余部分依次放入临时数组
 while (mid <= right) {
 tmpArr[third++] = data[mid++];
 }
 while (left <= center) {
 tmpArr[third++] = data[left++];
 }
 // 将临时数组中的内容拷贝回原数组中
 while (tmp <= right) {
 data[tmp] = tmpArr[tmp++];
 }
}

是不是很简单，在合并的时候是左右两部分进行合并。不过这里我们会发现有很多问题，比如说两个子序列就算合并起来也已经有序了，但是在代码中还是要一个一个比较。而且我们的子数组比较小的时候，归并排序的速度并没有显著提高。因此我们可以做出一些改进。

2、改进算法

针对上面出现的问题：我们可以在以下几个方面：

（1）如果子数组较小，改用插入排序；

（2）两个子数组若已经有序，则直接复制进数组

（3）通过交换参数来避免每次都要复制到辅助数组。

OK，我们看一下代码：

 private static void sort(Comparable[] a, Comparable[] aux,int low, int height){
 int mid = low + (height -low) / 2; 
 //改进1：若子序列比较短，则直接使用插入排序
 if(height <= low + 7 - 1){ 
 insertionSort(a, lo, hi);
 return;
 } 
 sort(aux,a,low,mid); 
 sort(aux,a,mid+1,height); 
 //less函数比较a[mid+1]和a[mid]的大小
 //改进2：如果数组已经有序则直接复制，不再merge
 if(!less(a[mid+1],a[mid])){ 
 System.arraycopy(aux, low, a, low, height-low+1);
 return;
 }
 merge(a,aux,low,mid,height); 
 }

还有一点改进是在merge函数中进行的，我们来看一下：

private void merge(Comparable[] a,Comparable[] aux, int lo, int mid, int hi){
 //左半部分
 for(int k = low; k <= mid; k++)
 aux[k] = a[k];
 //右半部分
 for(int k = mid+1; k <= height; k++)
 aux[k] = a[height+mid+1-k];
 int i = low, j = height; 
 //整个序列
 for(int k=low;k<=height; k++ ){
 if(less(aux[j],aux[i]))
 a[k] = aux[j--];
 else 
 a[k] = aux[i++]; 
 } 
}

插入算法在这里就不再演示了。下面我们就分析一下归并排序。

三、算法分析

我们分析的时候只考虑第一种情况，也就是基本情况。

归并排序的总时间=分解时间+解决问题时间+合并时间。

（1）分解时间：把待排序序列分解，时间为o(1)。

（2）解决问题时间：处理一个序列时间为1，处理两个子序列的时间就是1/2。

（3）合并时间：时间为o（n）。

所以总时间T(n)=2T(n/2)+o(n)=o(nlogn)。也就是说在最坏、最好、平均情况下时间复杂度均为o(nlogn)。