Simulink学习笔记之模型的配置仿真
一、解算器Solver
要仿真动态系统,可以计算其在指定时间跨度内连续时间步的状态。此计算使用系统模型提供的信息。时间步是发生计算的时间间隔。此时间间隔的大小称为步长大小。以这种方式计算模型状态的过程称为解算模型。没有任何一种模型解算方法能适用于所有系统。Simulink® 提供了一组程序,称为求解器。每个求解器代表一种特定的模型解算方法。
求解器运用一种数值方法来解算代表模型的一组常微分方程。通过这种计算,它确定下一个仿真步的时间。在解算此初始值问题的过程中,求解器还满足您指定的准确性要求。
数学家们开发出了多种数值积分方法来解算表示动态系统连续状态的常微分方程 (ODE)。提供了一套全面的固定步长和可变步长连续求解器,其中每个求解器实现一种特定的 ODE 解法(请参阅比较求解器)。在模型配置参数的 Solver 窗格中选择求解器。
Solver是Simulink的重要组成部分,集成不同的数值解算方法。解算器有如下分类。
| 求解器类型 | 显式/隐式 | 离散 | 连续 | 变阶 |
|---|---|---|---|---|
| 固定步长 | 显式 | 不适用 | Fixed-Step Continuous Explicit Solvers | 不适用 |
| 隐式 | 不适用 | Fixed-Step Continuous Implicit Solvers | 不适用 | |
| 可变步长 | 显式 | Variable Step Solvers in Simulink | Variable-Step Continuous Explicit Solvers | 单阶与变阶连续求解器 |
| 隐式 |
| Variable-Step Continuous Implicit Solvers | 单阶与变阶连续求解器 |
1、固定、可变步长解算器
步长为两个相邻点之间的时间间隔。固定和可变步长没有绝对的优劣势。
注意:在嵌入式代码中,需要采用固定步长解算器
为方便理解,做如下实验:
(1)搭建一个简单的正弦波形仿真模型
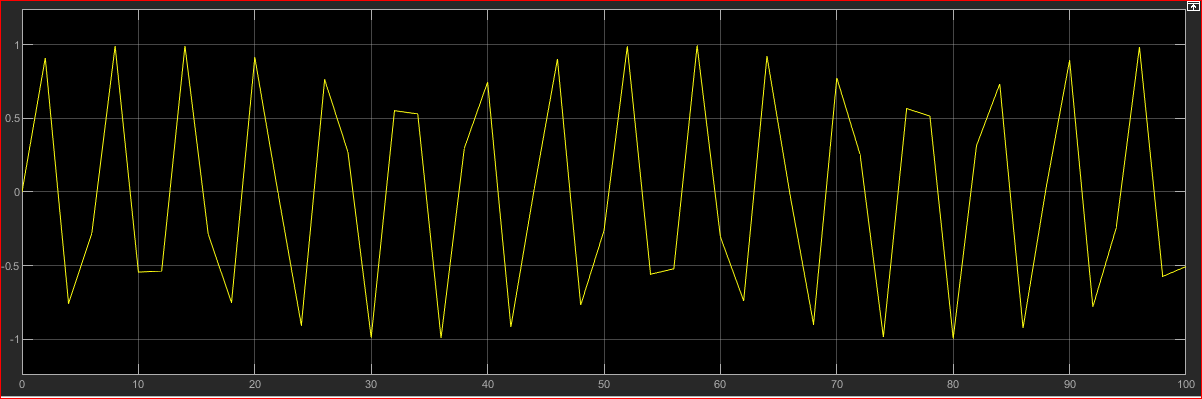
(2)可变步长的波形图
对其进行如下设置:
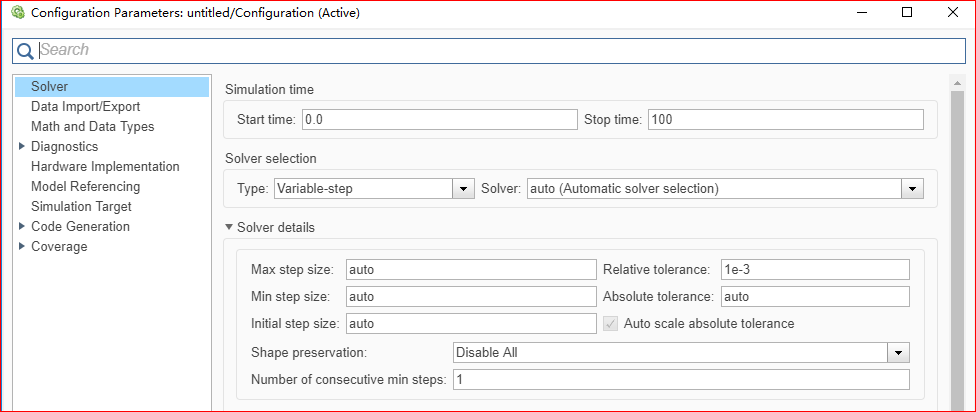
其波形如下图所示

(3)改为固定步长
更改配置,如下图所示,改为固定步长,步长为0.1
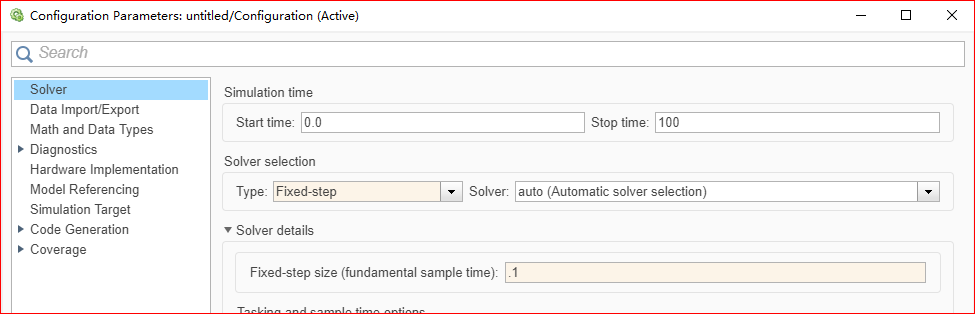
生成的sin图形为下图所示
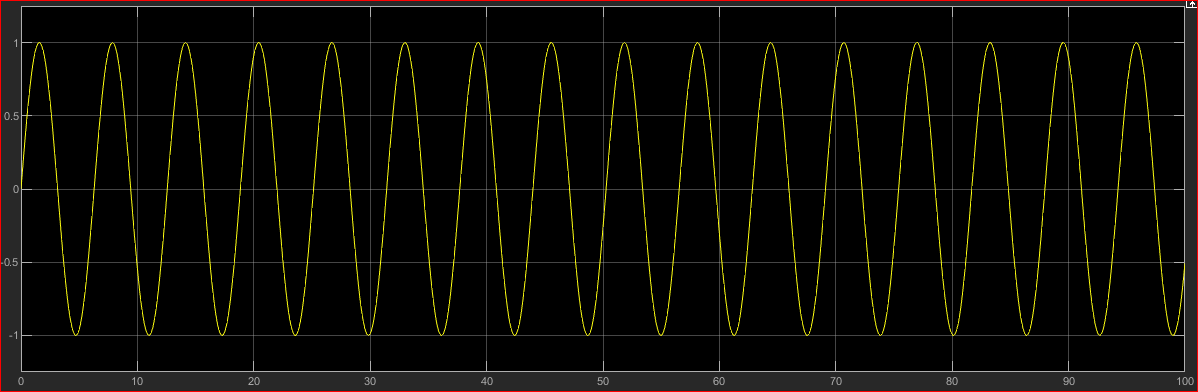
2、连续与离散求解器
Simulink 同时提供连续和离散求解器。
两组求解器都包括离散求解器和连续求解器。离散和连续求解器依赖于模型的模块来计算任何离散状态的值。定义离散状态的模块负责计算这些状态在每个时间步的值。
连续求解器运用数值积分方法来计算模块定义的连续状态。
选择求解器时,首先要确定是要使用离散求解器,还是要使用连续求解器。
如果模型没有连续状态,Simulink 将切换到固定步长离散求解器或可变步长离散求解器。
如果模型只有连续状态,或者同时具有连续状态和离散状态,根据模型的动态特性从其余的求解器选项中选择一种连续求解器。否则,将产生错误。
连续求解器使用数值积分方法,根据模型在之前的时间步的状态和状态导数来计算模型在当前时间步的连续状态。连续求解器依赖单个模块来计算模型在每个时间步的离散状态值。
离散求解器主要用于解算纯离散模型。它们只计算模型的下一个仿真时间步。执行这种计算时,它们依赖于模型中的每个模块来更新其各个离散状态。它们不计算连续状态。
注意
您必须使用连续求解器来解算同时包含连续和离散状态的模型,因为离散求解器无法处理连续状态。另一方面,如果您对没有状态或只具有离散状态的模型选择连续求解器,Simulink 软件将使用离散求解器。
3、显示、隐示解算器
可以用以下方程表示显式系统:
˙x=f(x)
对于任何给定的 x 值,您可以通过代换 f(x) 中的 x 并求解该方程来计算 ˙x。
F(˙x,x)=0
形式的方程被认为是隐式的。对于任何给定的 x值,您必须求解此方程来计算 x。线性隐式系统可以用以下方程表示
M(x).˙x=f(x)
M(x) 称为质量矩阵,f(x)是外力函数。当您在模型中使用物理建模模块时,系统将变成线性隐式系统。
虽然使用隐式或显式连续求解器都可以解算所有这些系统,但隐式求解器专为解算刚性问题而设计。显式求解器用于解算非刚性问题。对于常微分方程问题,如果所需的解变化缓慢,但存在变化很快的较接近解,则称为刚性问题。数值方法必须执行较小的时间步来解算此类系统。刚度涉及到效率问题。系统的刚度越强,显式求解器执行计算的时间越长。刚性方程组具有缓慢变化和快速变化两种连续动态。
与显式求解器相比,隐式求解器为振动行为提供更高的稳定性。但是,隐式求解器的计算开销也更高。它们在每个时间步使用类牛顿法生成 Jacobian 矩阵并解算一组代数方程。
4、单步、多步解算器
Simulink 求解器库中提供了单步和多步求解器。单步求解器使用上一个时间点
![]()
的解以及 tn 与 tn-1 之间的多个点的导数值来估算
![]()
。这些点是子时间步。
多步求解器使用前面几个时间步的结果来计算当前解。Simulink 提供一个显式多步求解器 ode113 和一个隐式多步求解器 ode15s。二者都是可变步长求解器。
5、变阶解算器
这种区分基于求解器解算方程组时使用的阶次。求解器库中包含两个变阶求解器
ode15s和 ode113。它们使用多阶来解算方程组。具体来讲,隐式可变步长 ode15s求解器使用一阶到五阶方程,而显式可变步长 ode113求解器使用一阶到十三阶方程。对于 ode15s,您可以通过 Maximum Order参数限制应用的最高阶次。
6、解算器的选用
求解器通过使用模型提供的信息,计算动态系统在指定时间范围内连续时间步的状态,从而对动态系统进行仿真。根据系统模型计算系统连续状态的过程称为解算模型。没有任何一种模型解算方法可满足所有系统需要。
最后
以上就是神勇悟空最近收集整理的关于Simulink学习笔记之模型的配置仿真Simulink学习笔记之模型的配置仿真一、解算器Solver 的全部内容,更多相关Simulink学习笔记之模型内容请搜索靠谱客的其他文章。








发表评论 取消回复