目录

一、二维曲线

1.plot函数

plot函数的基本用法

最简单的plot函数调用格式

plot(x,y)函数参数的变化形式

含选项的plot函数

2.fplot函数

fplot函数的基本用法

二、绘制图形的辅助操作

1.图形标注

title函数

xlabel函数和ylabel函数

text函数和gtext函数

2.坐标控制

axis函数的其他用法

给坐标系加网格和边框

图形保持

3.图形窗口的分割

三、其他形式的二维曲线

1.其他坐标系下的二维曲线图

极坐标图

2.统计图

条形类图形

直方图

面积类图形

散点类图形

矢量类图形

四、三维曲线

1.plot3函数

plot3函数的基本用法：

plot3函数参数的变化形式

含多组输入参数的plot3函数

2.fplot3函数

五、三维曲面

1.平面网格数据的生成

利用矩阵运算生成

利用meshgrid函数生成

2.绘制三维曲面的函数

mesh（x，y，z，c）

surf（x，y，z，c）

3.标准三维曲面

sphere函数

cylinder函数

peaks函数

4.fsuf函数和fmesh函数

六、图形修饰处理

1.视点处理

view函数的基本用法

view函数的其他用法

2.色彩处理

颜色的向量表示

色图（Colotmap）

三维图形表面的着色

3.图形的裁剪处理

七、交互式绘图工具

1.“绘图”选项卡

显示绘图工具

绘图工具的组成

小结

---

 

 

一、二维曲线

 

plot函数

fplot函数

 

1.plot函数

 

plot函数的基本用法

plot（x，y）

其中x和y分别用于存储x坐标和y坐标数据。

 

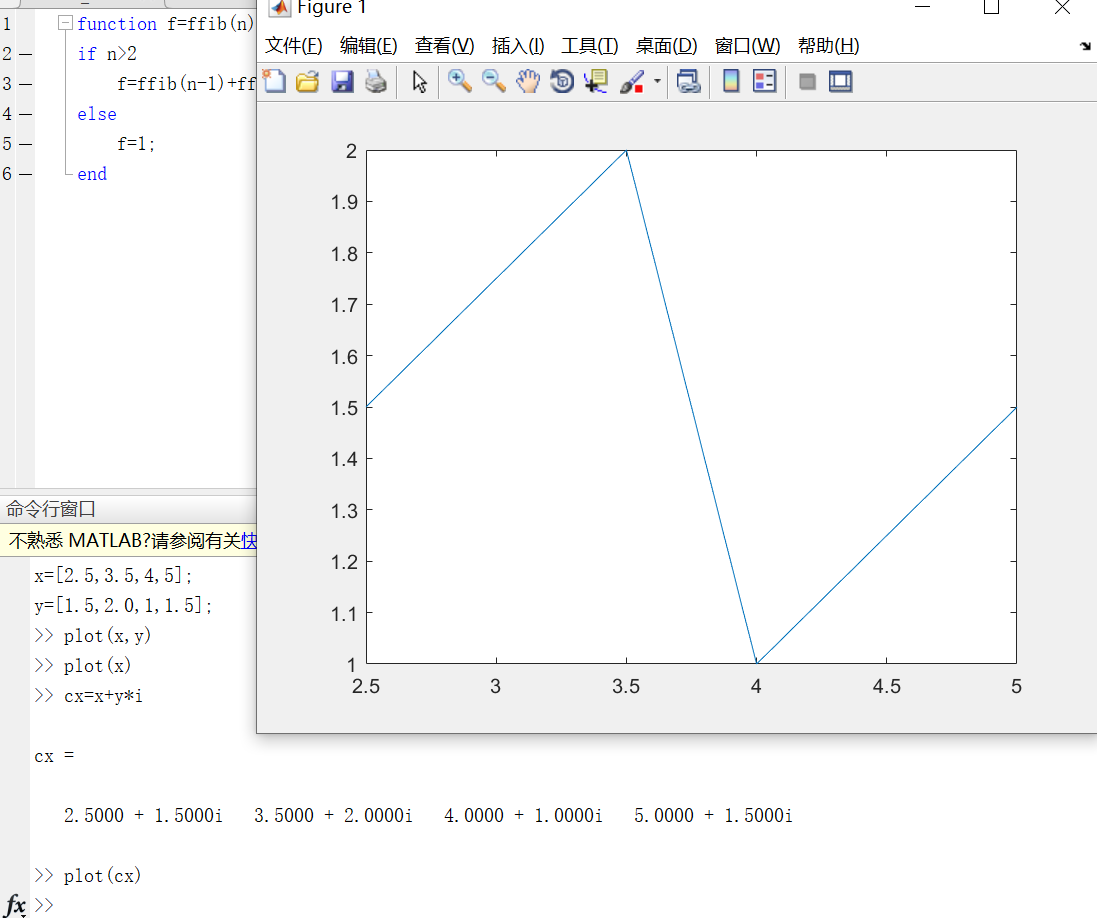
代码：

x=[2.5,3.5,4,5];
y=[1.5,2.0,1,1.5];
>> plot(x,y)

绘图如下：

 

 

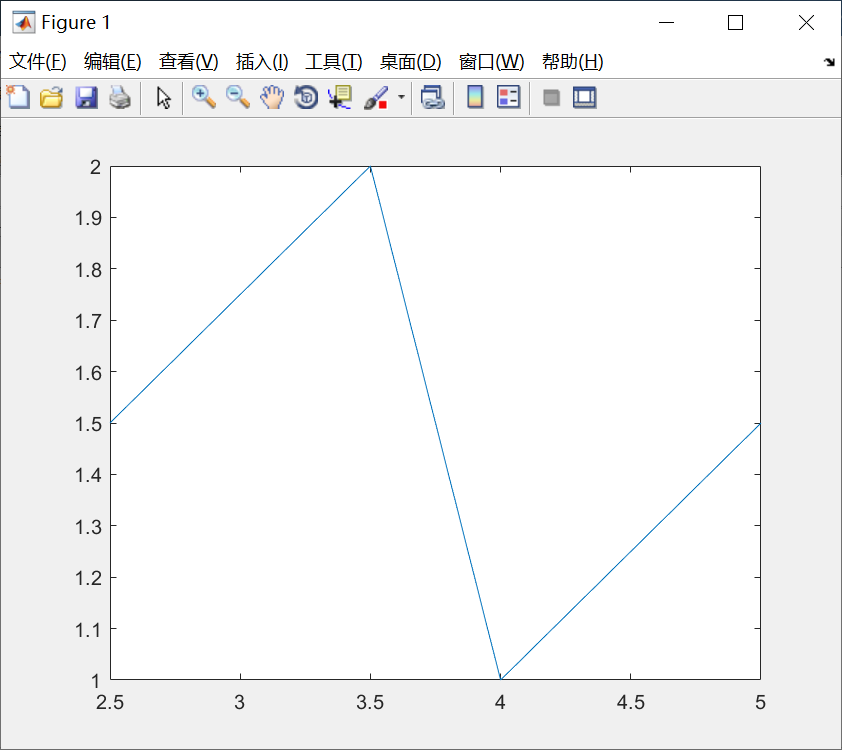
最简单的plot函数调用格式

 

>> plot(x)  也可以直接这样简单调用。

图像

 

当plot函数的参数x是复数向量时，则分别以该向量元素实部和虚部为横、纵坐标绘制出一条曲线。

 

代码：

 

也可以使用cx=complex（x，y）；

 

plot(x,y)函数参数的变化形式

 

当x是向量，y是矩阵时：

• 如果矩阵y的列数等于x的长度，则以向量x为横坐标，以y的每个行向量为纵坐标绘制曲线，曲线的条数等于y的行数。
• 如果矩阵y的行数等于x的长度，则以向量x为横坐标，以y的每个列向量为纵坐标绘制曲线，曲线的条数等于y的列数。

 

例子：

 

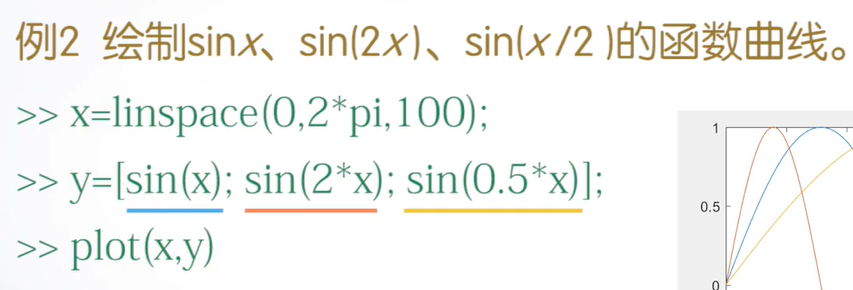
绘制的图形如下：

 

 

 

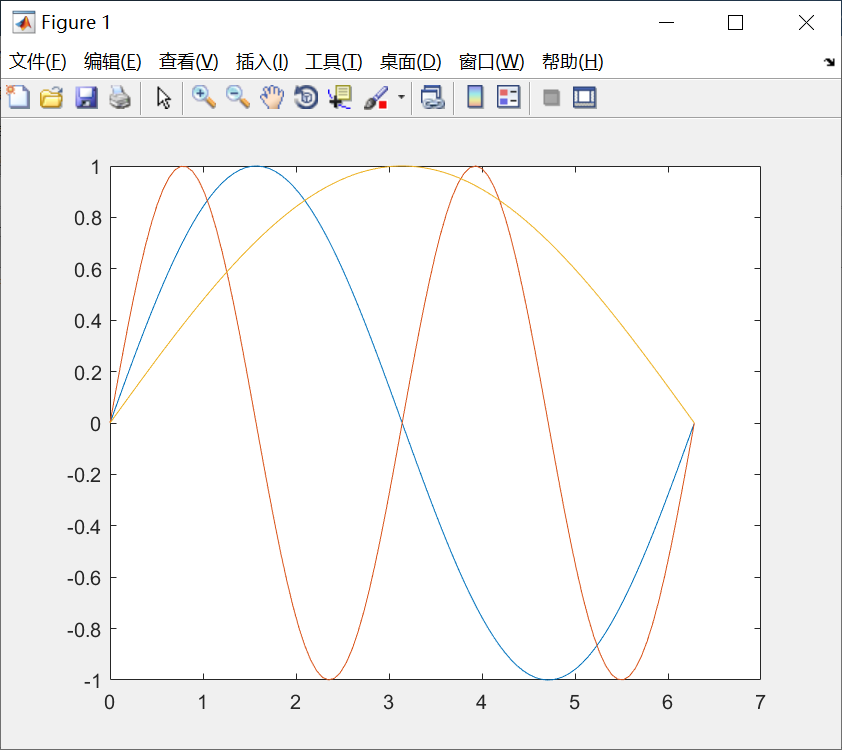
当x、y是同型矩阵时，以x、y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。

另一种方案：

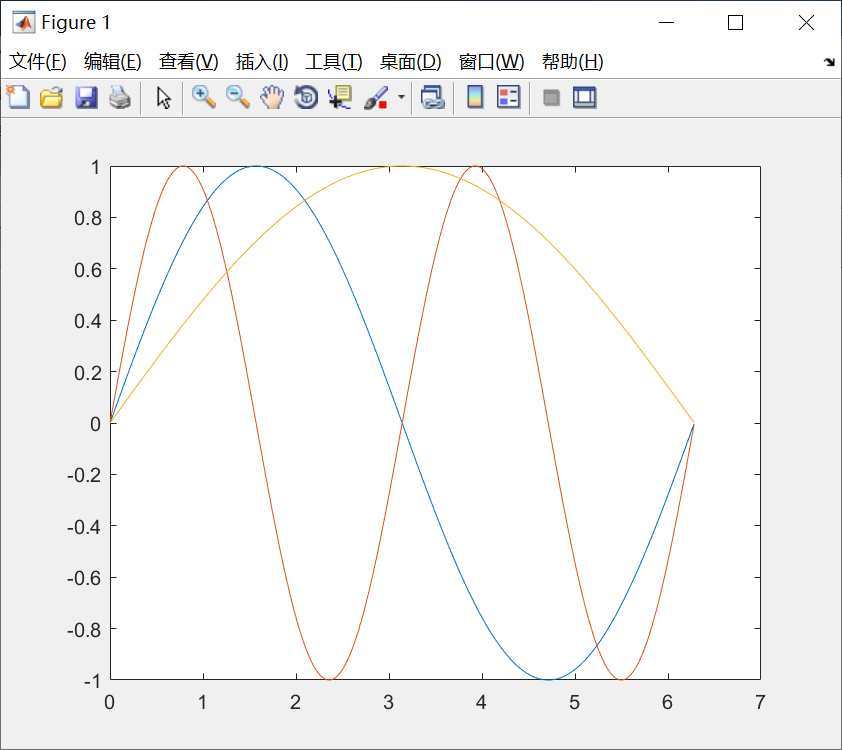
>> t=0:0.01:2*pi;
>> t1=t';
>> x=[t1,t1,t1];
>> y=[sin(t1),sin(2*t1),sin(0.5*t1)];
>> plot(x,y)

 

图像结果：

 

含多个输入参数的plot函数

plot（x1，y1，x2，y2，···，xn，y，n）

其中每一向量对构成一组数据点的横、纵坐标，绘制一条曲线。

 

例子：

 

 

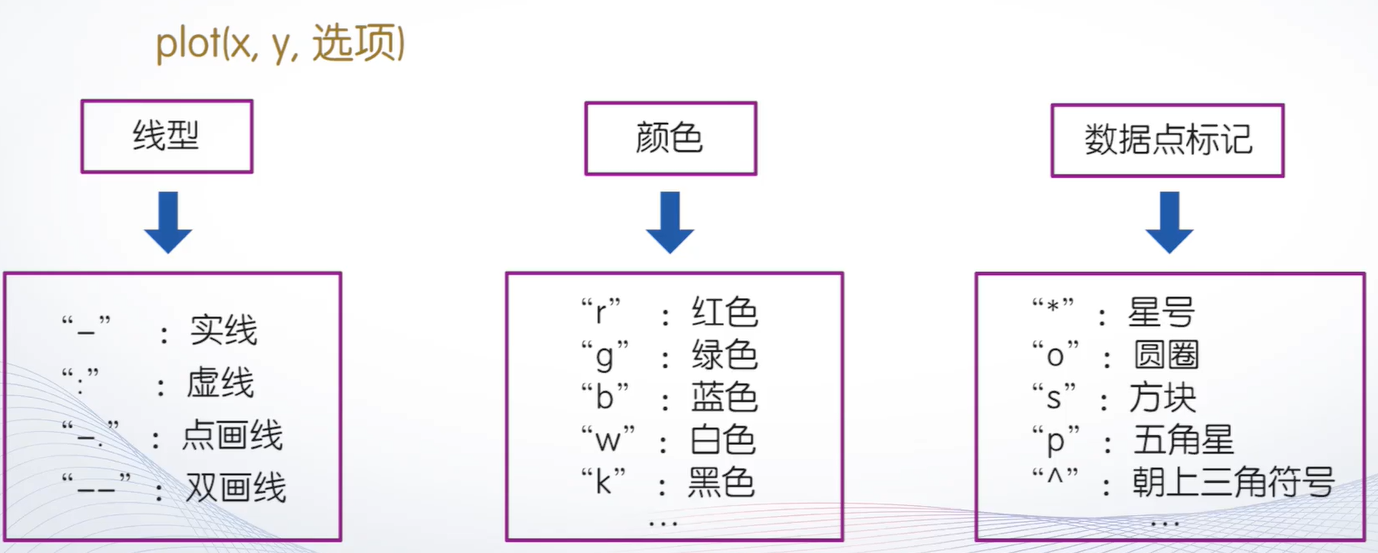
含选项的plot函数

plot（x，y，选项）

 

 

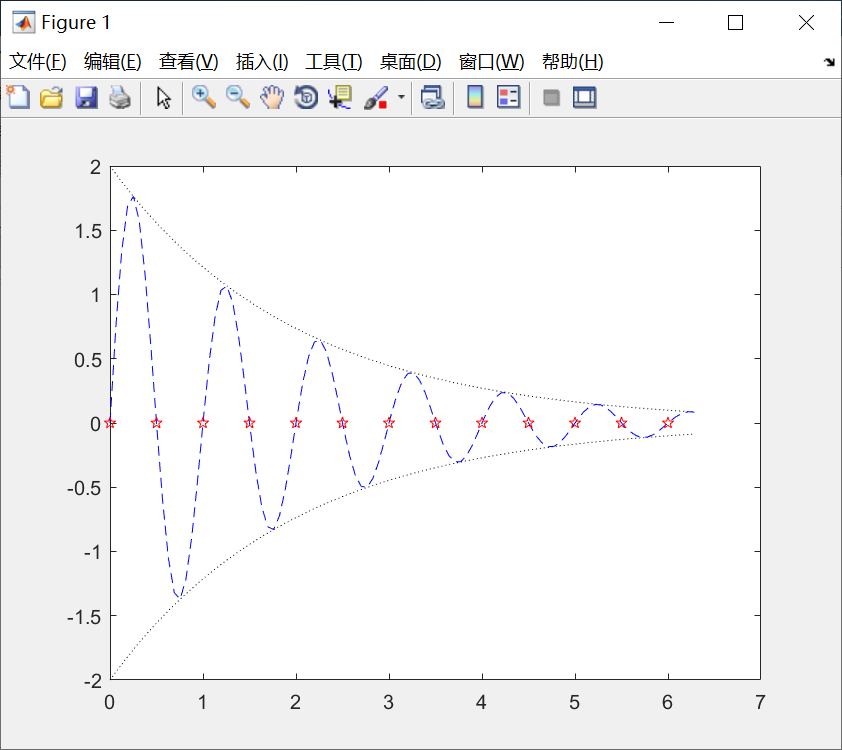
例子：

 

>> x=(0:pi/50:2*pi)';
>> y1=2*exp(-0.5*x)*[1,-1];
>> y2=2*exp(-0.5*x).*sin(2*pi*x);
>> x1=0:0.5:6;
>> y3=2*exp(-0.5*x1).*sin(2*pi*x1);
>> plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp')

图像：

 

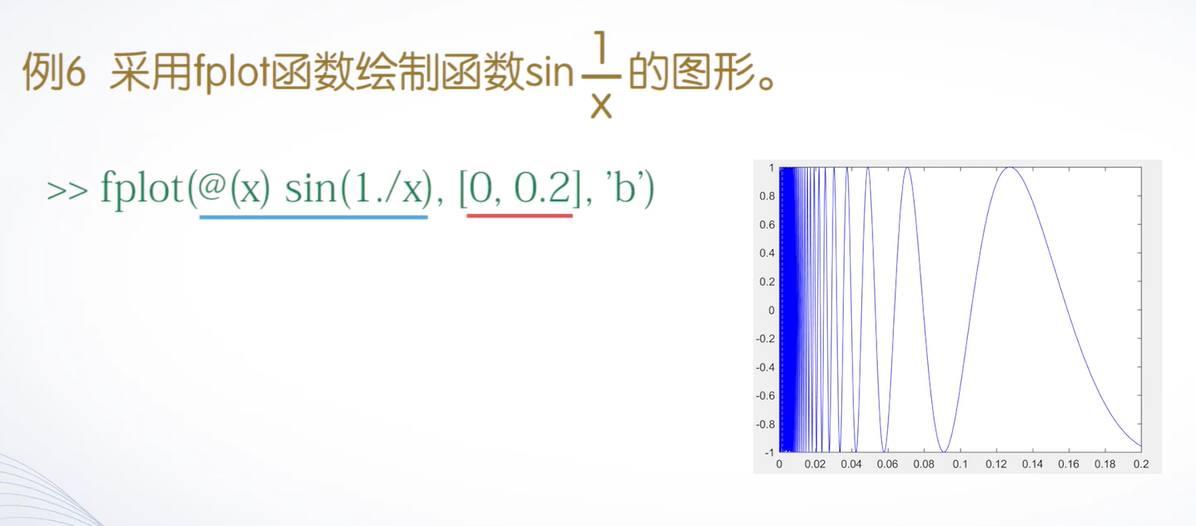
2.fplot函数

 

fplot函数的基本用法

 

fplot（f，lims，选项）

其中，f代表一个函数，通常采用函数句柄的形式。lims为x轴的取值范围，用二元向量[xmin，xmax]描述，默认值为[-5,5]。选项定义与plot函数相同。

 

例子：

 

双输入函数参数的用法

fplt（funx，funy，tlims，选项）

其中，funx、funy代表函数，通常采用函数句柄的形式。tlims为参数函数funx和funy的自变量的取值范围，用二元向量[tmin,tmax]描述。

例子：

 

二、绘制图形的辅助操作

 

给图形添加标注

坐标控制

图形保持

图形窗口的分割

 

1.图形标注

 

title（图形标题）

xlabel（x轴说明）

ylabel（y轴说明）

text（x，y，图形说明）

legend（图例1，图例2，···）

 

title函数

 

 

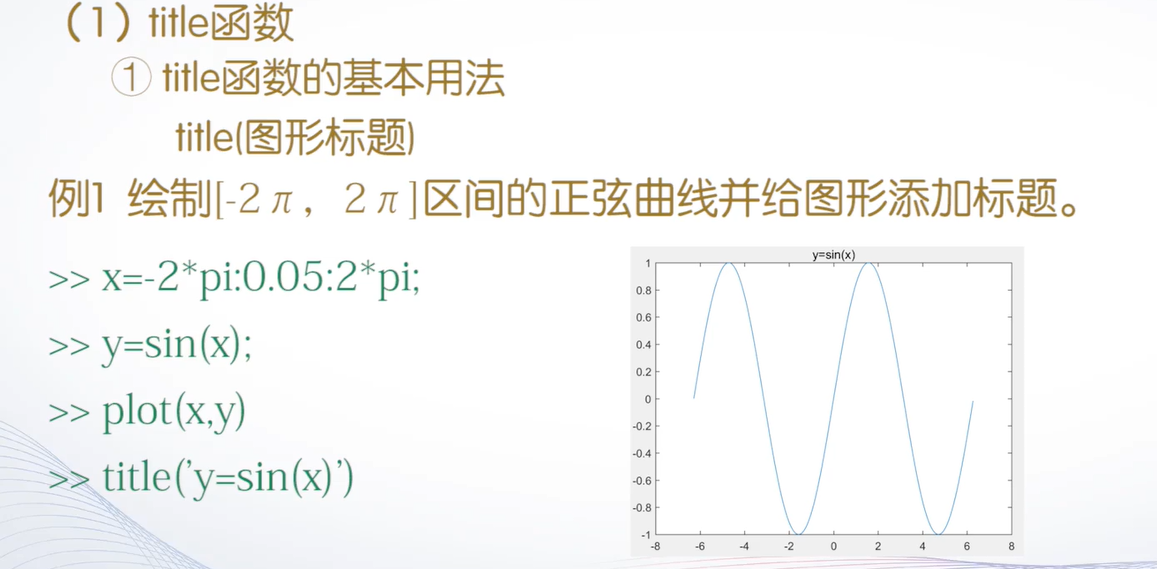
如果多行标题的话

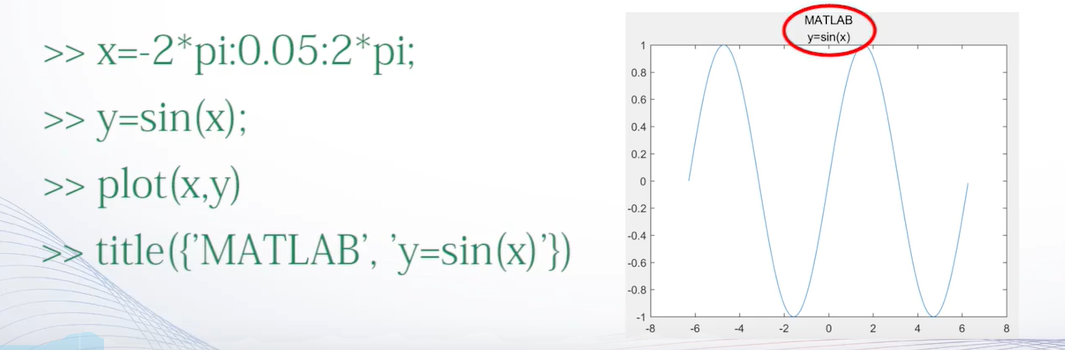
在图形标题中使用LaTeX格式控制符

 

含有属性设置的title函数

 

 

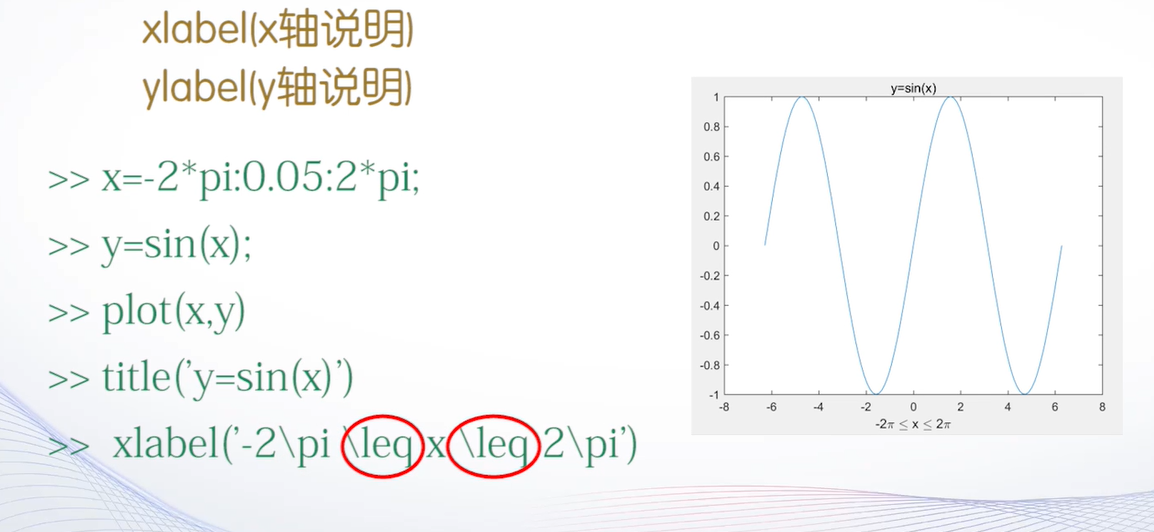
xlabel函数和ylabel函数

xlabel（x轴说明）

ylabel（y轴说明）

 

 

text函数和gtext函数

 

text（x，y，说明）

gtext（说明）

 

 

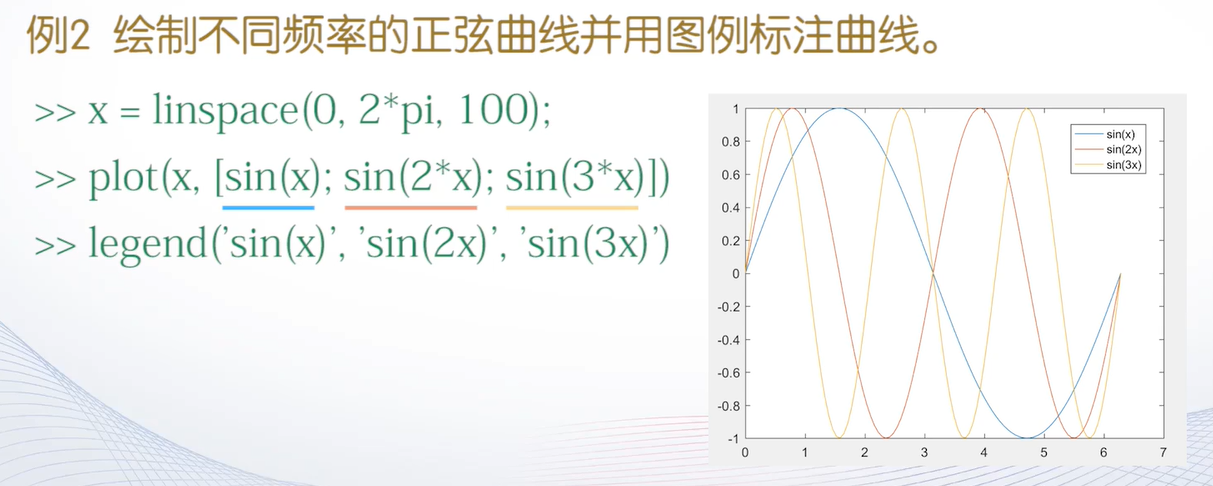
legend函数

lgend（图例1，图例2，···）

 

例子：

 

2.坐标控制

 

 

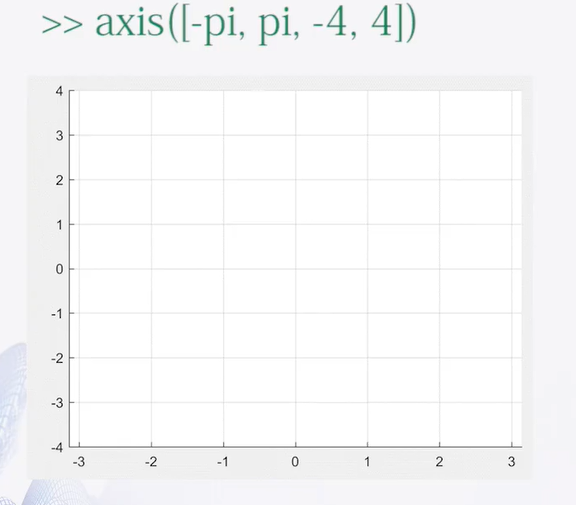
axis函数的其他用法

• axis equal：纵、横坐标轴采用灯长刻度
• axis square：产生正方形坐标系（默认为矩形）
• axis auto：使用默认设置
• axis off：取消坐标轴
• axis on：显示坐标轴

 

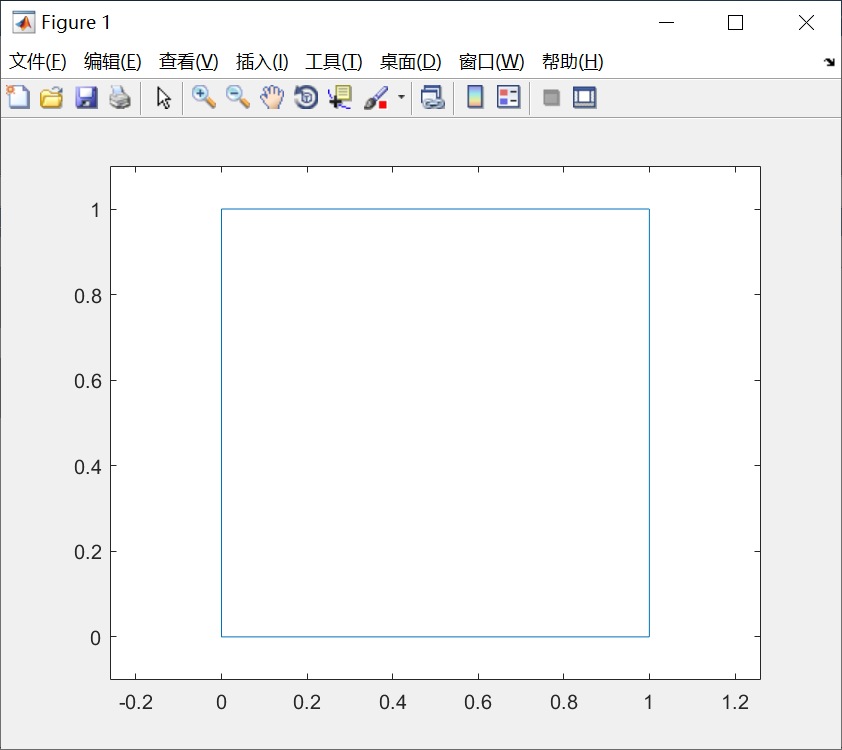
代码：

x=[0,1,1,0,0];
y = [0,0,1,1,0];
plot(x,y)
axis([-0.1,1.1,-0.1,1.1])
axis equal;

图形：

 

 

给坐标系加网格和边框

 

grid on   控制显示网格线

grid off    控制不显示网格线

grid          两种状态之间切换

没有出现grid，默认不显示网格线

 

box on

box off

box    

和grid用法相同，如果没有出现box命令，默认显示边框线。

 

例子：

代码：

x = linspace(0,2*pi,100);
y = [sin(x);sin(2*x);sin(0.5*x)];
plot(x,y)
axis([0,7,-1.2,1.2])
title('不同频率正弦函数曲线');
xlabel('Variable X');
ylabel('Variable Y');
text(2.5,sin(2.5),'sin(x)');
text(1.5,sin(2*1.5),'sin(2x)');
text(5.5,sin(0.5*5.5),'sin(0.5x)');
legend('sin(x)','sin(2x)','sin(0.5x)');
grid on

图像：

 

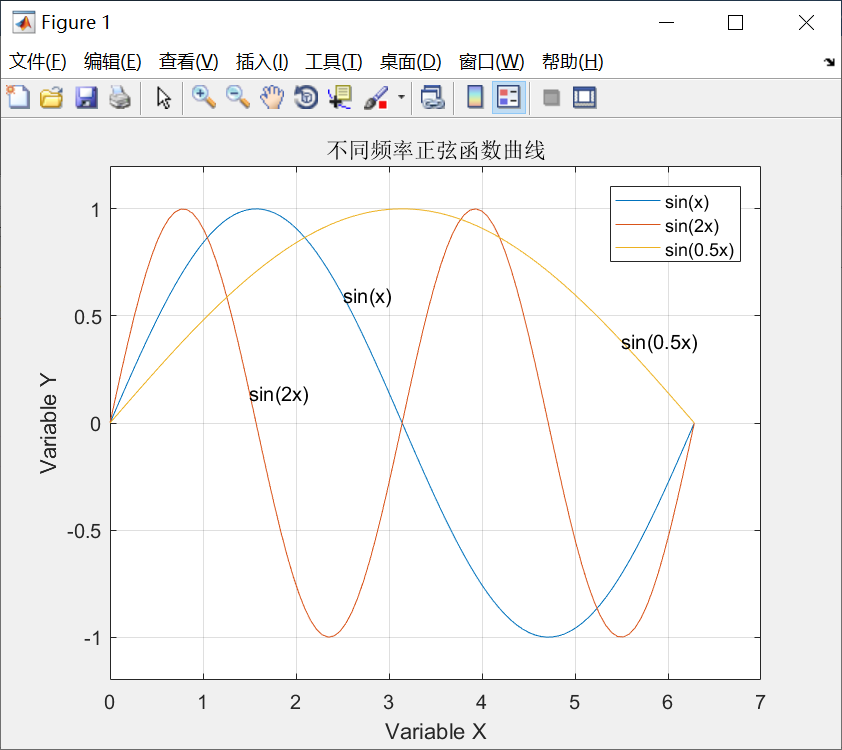
图形保持

一般情况下，绘图命令每执行一次，就会刷新一次窗口，窗口原有图形将不会存在，可以使用hold命令

hold on命令：控制保持原有图形；

hold off命令：控制刷新图形窗口；

hold命令：控制在两种状态之间进行切换；

 

例子：用图形保持功能绘制两个同心圆。

代码：

t = linspace(0,2*pi,100);
x = sin(t);
y = cos(t);
plot(x,y,'b');
hold on;
plot(2*x,2*y,'r--');
grid on;
axis([-2.2,2.2,-2.2,2.2]);
axis equal;

图形：

 

 

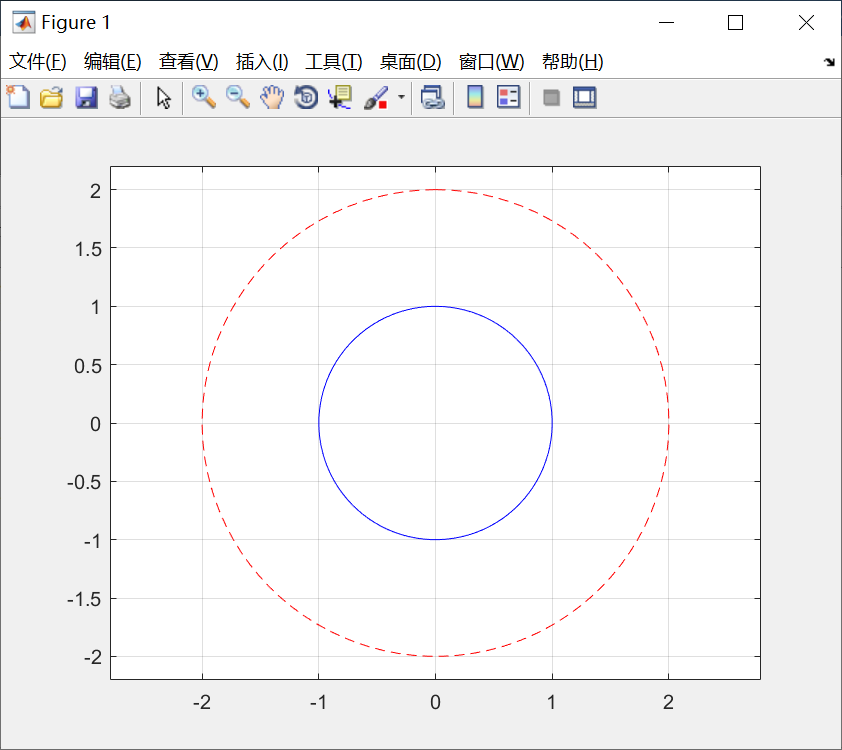
3.图形窗口的分割

子图：同一图形窗口中的不同坐标系下的图形称为子图。

subplot函数

subplot（m，n，p）

其中，m和n指定将图形窗口分成m*n个绘图区，p指定当前活动区。

 

例子：

代码：

x = linspace(0,2*pi,60);
subplot(2,2,1);
plot(x,sin(x)-1);
title('sin(x)-1');
axis([0,2*pi,-2,0])
subplot(2,1,2)
plot(x,cos(x)+1);
title('cos(x)+1');
axis([0,2*pi,0,2]);
subplot(4,4,3);
plot(x,tan(x));
title('tan(x)');
axis([0,2*pi,-40,40]);
subplot(4,4,8);
plot(x,cot(x));
title('cot(x)');
axis([0,2*pi,-35,35]);

 

图形：

 

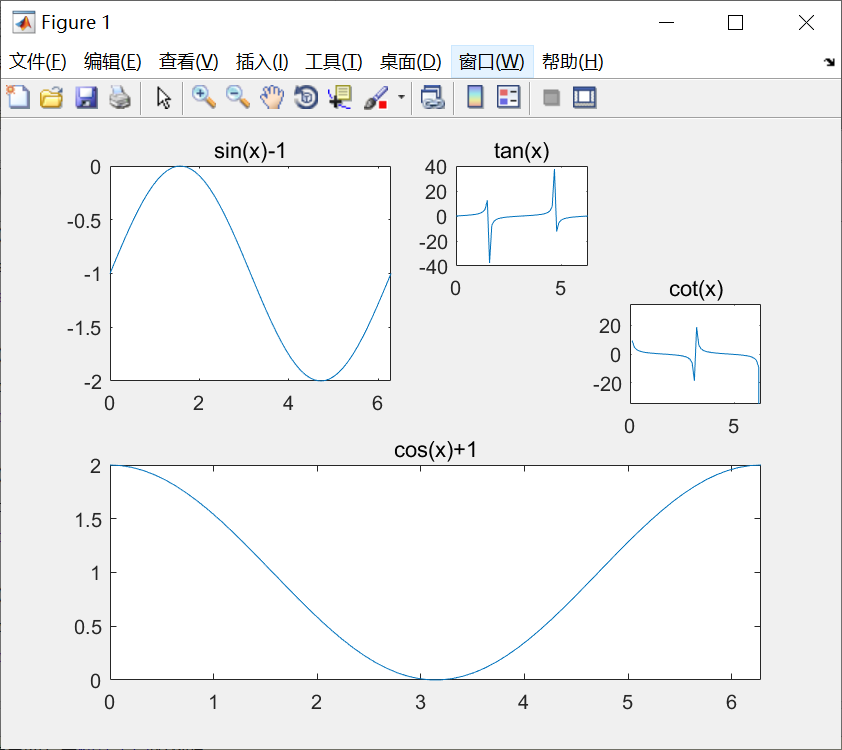
三、其他形式的二维曲线

 

其他坐标系下的二维曲线图

统计图

矢量图形

 

1.其他坐标系下的二维曲线图

 

semilogx（x1，y1，选项1，x2，y2，···）

semilogy（x1，y1，选项1，x2，y2，选项2，···）

loglog（x1，y1，选项1，x2，y2，选项2，···）

 

例子：绘制1/x的直角线性坐标图和三种对数坐标图。

x = 0:0.1:10;
y = 1./x;
subplot(2,2,1);
plot(x,y);
title('plot(x,y)');
subplot(2,2,2);
semilogx(x,y);
title('semilogx(x,y)');
grid on;
subplot(2,2,3);
semilogy(x,y);
title('semilogy(x,y)');
grid on;
subplot(2,2,4);
loglog(x,y);
title('loglog(x,y)');
grid on;

 

图形：

 

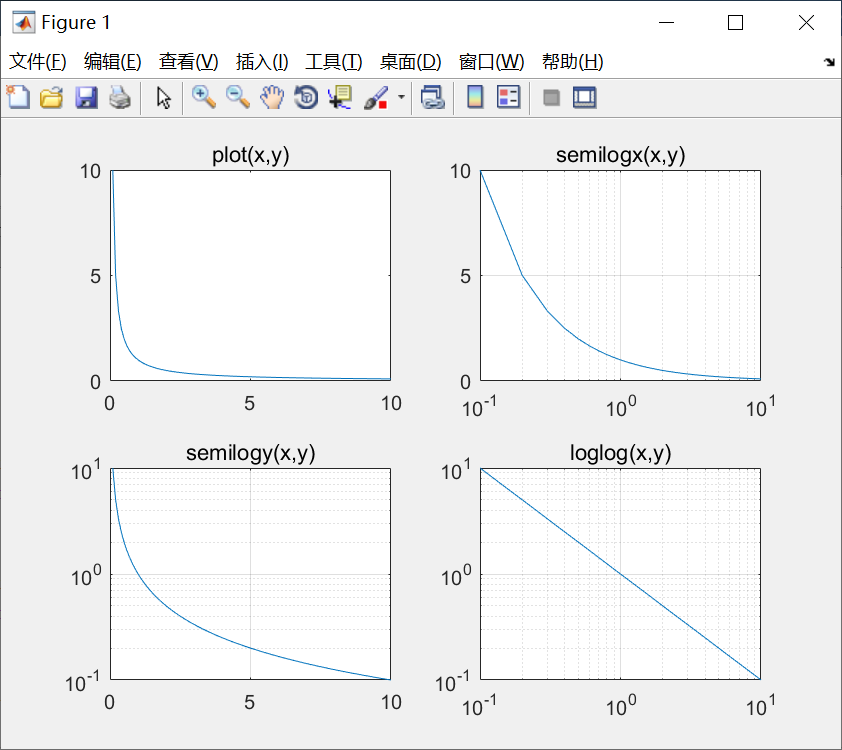
极坐标图

polar（theta，rho，选项）

其中，theta为极角，rho为极径，选项的内容与plot函数相同。

例子：

 

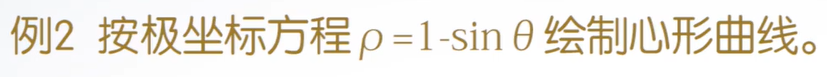
代码：

t = 0:pi/100:2*pi;
r = 1-sin(t);
subplot(1,2,1);
polar(t,r);
subplot(1,2,2);
t1 = t-pi/2;
r1 = 1-sin(t1);
polar(t,r1);

 

图像：

 

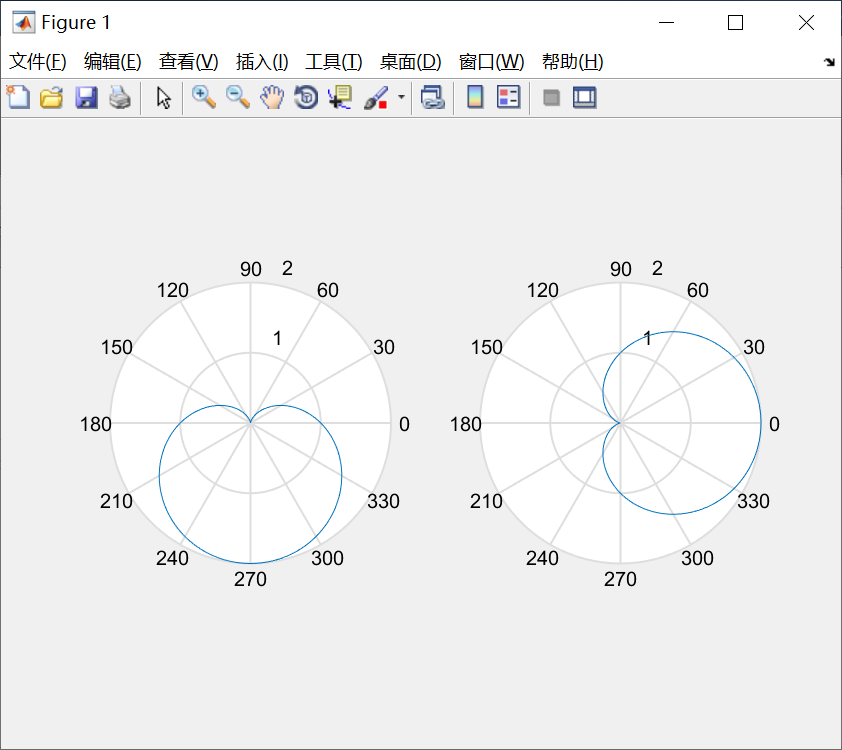
2.统计图

 

条形类图形

条形图

• bar函数
• barh函数

 

bar函数

bar（y，style）

其中，参数y是数据，选项style用于指定分组排列模式。

例子：绘制分组条形图：

y=[1,2,3,4,5;1,2,1,2,1;5,4,3,2,1];
subplot(1,2,1);
bar(y);
title('Group');
subplot(1,2,2);
bar(y,'stacked');
title('Stack');

图像：

 

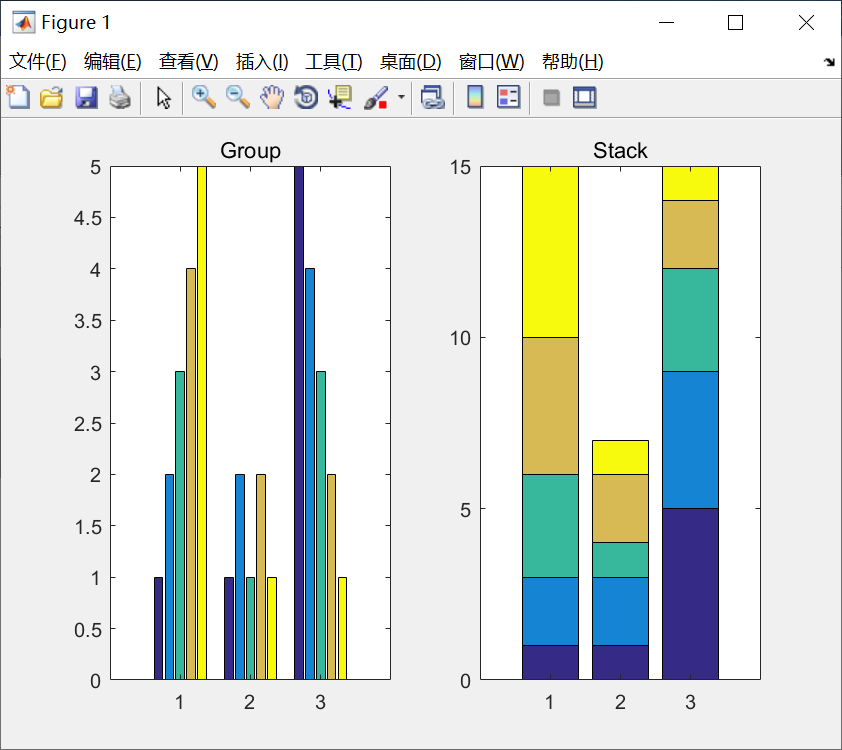
bar函数的另一种形式

bar（x，y，style）

其中，x存储横坐标，y存储数据。

 

例子：

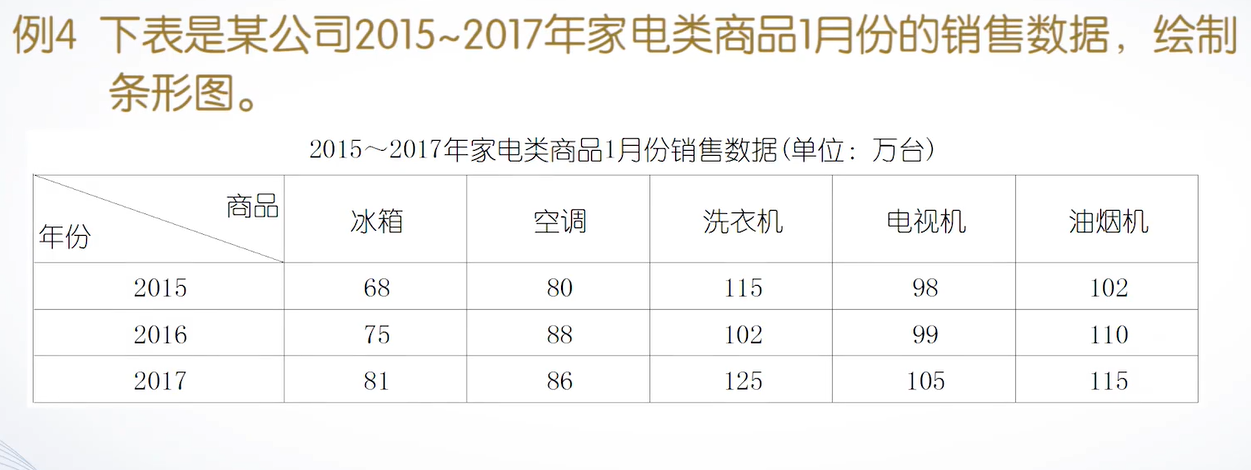
代码：

x=[2015,2016,2017];
y=[68,80,115,98,102;75,88,102,99,110;81,86,125,105,115];
bar(x,y);
title('Group');

图像:

 

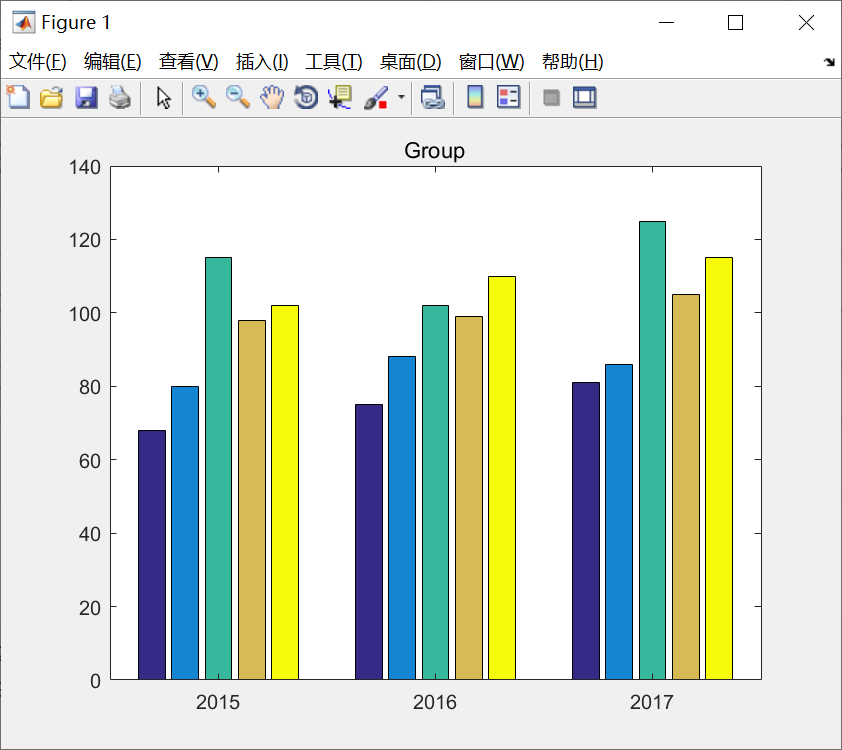
直方图

 

hist函数：直角坐标系下的直方图

rose函数：用于绘制极坐标下的坐标图。

 

hist函数

hist（y）

hist（y，x），第二个x用于设置统计区间的划分方式。若为标量：等分成x个小区间，若为向量，则向量的每一个数字指定每个区间的中心值，元素的个数为数据的分组数。x缺少时，默认按照10个等分区间等分。

其中，参数y是要统计的数据，x用于指定区间的划分方式。

 

例子：绘制服从高斯分布的直方图。

y=randn(500,1);
subplot(2,1,1);
hist(y);
title('高斯分布直方图');
subplot(2,1,2);
x=-3:0.2:3;
hist(y,x);
title('指定区间中心点的直方图');

图像：

 

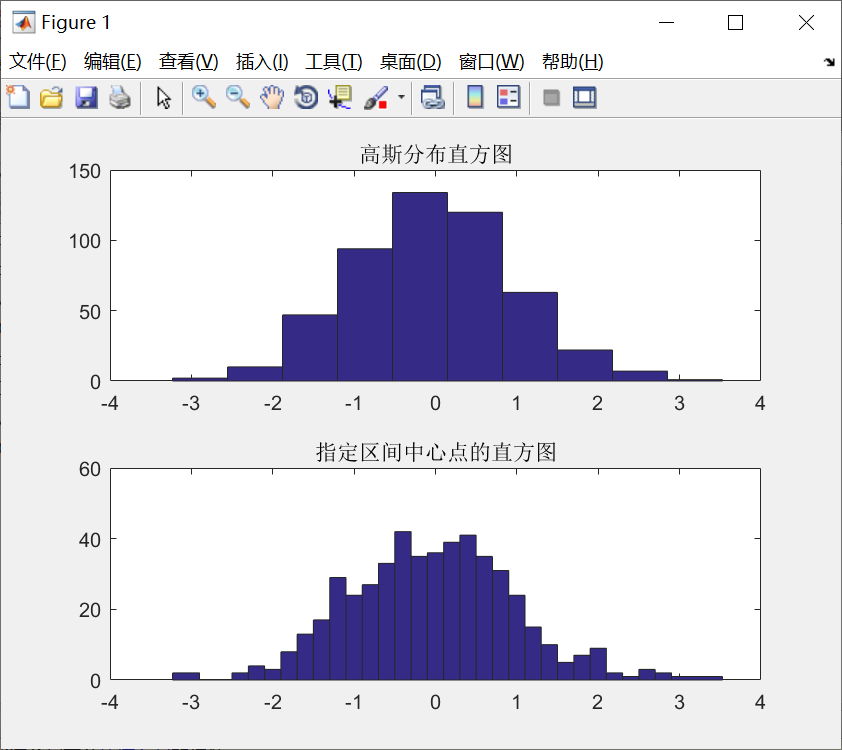
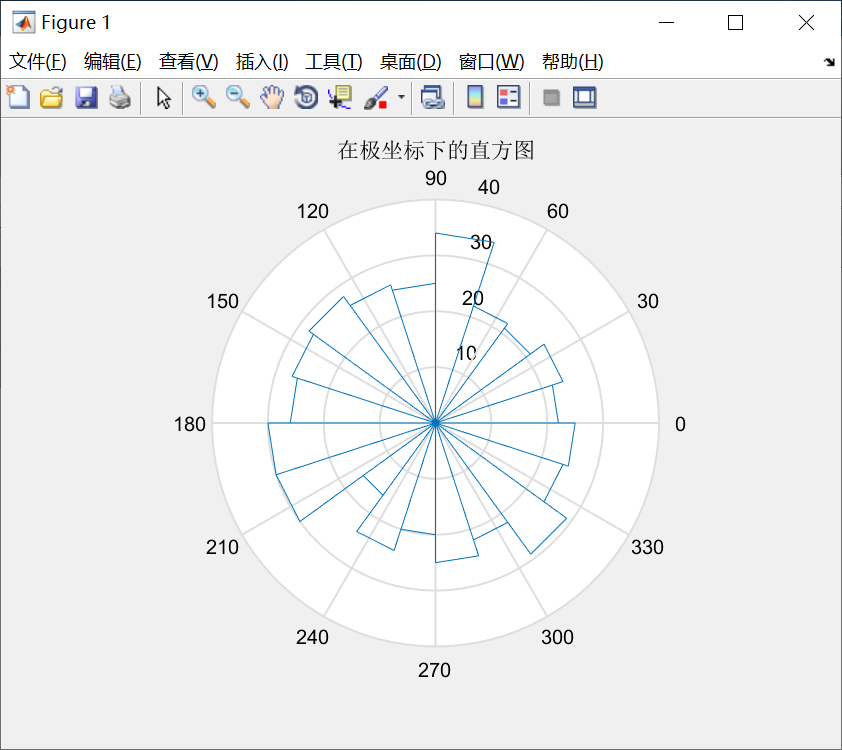
rose函数

用于绘制极坐标系下的直方图

rose（theta，x）

其中，参数theta是一个向量，用于确定每一区间与原点的角度，选项x用于指定区间的划分方式。若x为标量，则在0到2pi内均匀的划分成为x个区域，x缺少时，默认按20个等分区间划分。

例子：绘制高斯分布数据在极坐标下的直方图。

代码：

y=randn(500,1);
theta=y*pi;
rose(theta);
title('在极坐标下的直方图');

图形：

 

面积类图形

 

扇形图   pie函数

面积图   area函数

 

pie函数

pie（x，explode）

其中，参数x存储待统计数据，选项explode控制图块的显示模式。通常x为向量，绘图时x每一个元素对应一个扇形，每个扇形对应的幅度角度对应着所占的比重。

 

例子：

 

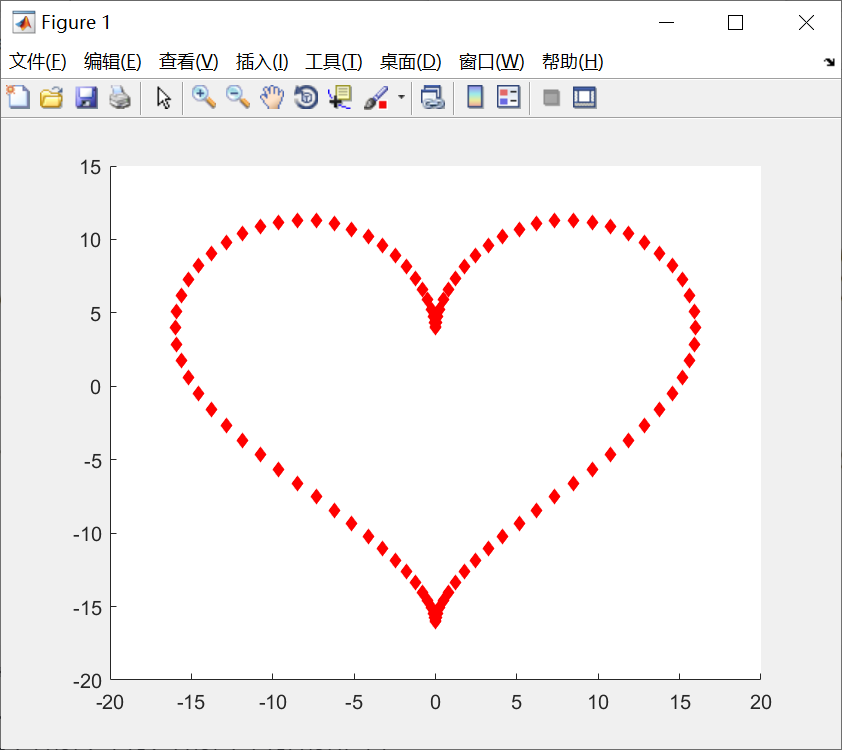
散点类图形

 

scatter函数：散点图

stairs函数：阶梯图

stem函数：杆图

 

scatter函数

scatter（x，y，选项，‘filled’）

参数x、y用于定位数据点，通常为向量，选项用于指定线型、颜色、数据点标记。

 

例子：

代码：

t = 0:pi/50:2*pi;
x = 16*sin(t).^3;
y = 12*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t);
scatter(x,y,'rd','filled');

图形：

 

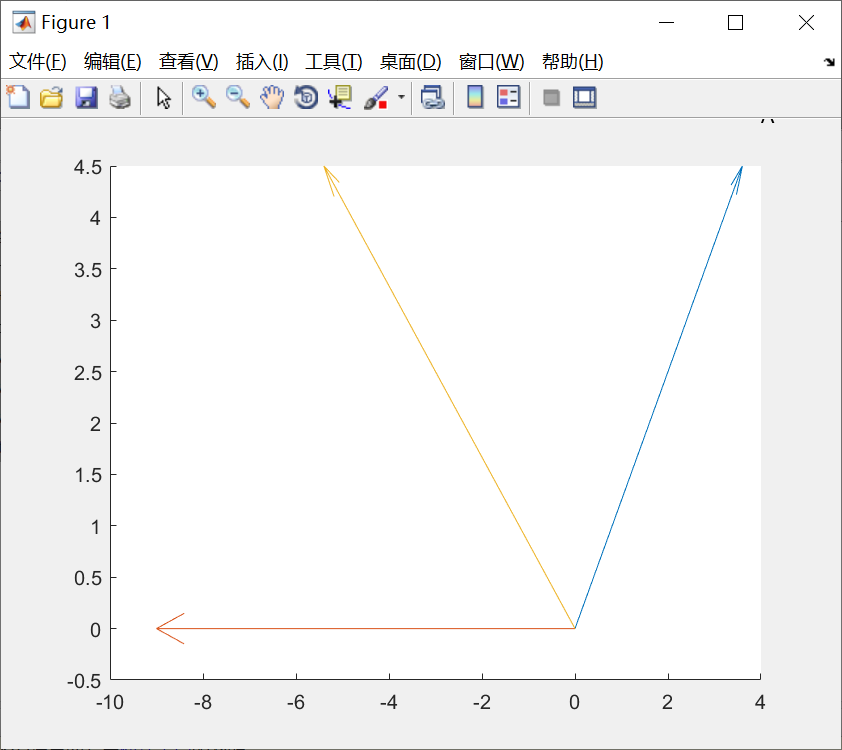
矢量类图形

 

compass函数：罗盘图

feather函数：羽毛图

quiver函数：箭头图

 

quiver（x，y，u，v）

其中，（x，y）指定矢量起点，（u，v）指定矢量终点。xyuv为同样大小的向量，或者同型的矩阵。

例子：

已知向量A、B，求A+B，并用矢量图表示。

 

代码：

A=[4,5];
B=[-10,0];
C=A+B;
hold on;
quiver(0,0,A(1),A(2));
quiver(0,0,B(1),B(2));
quiver(0,0,C(1),C(2));
text(A(1),A(2),'A');

图像：

 

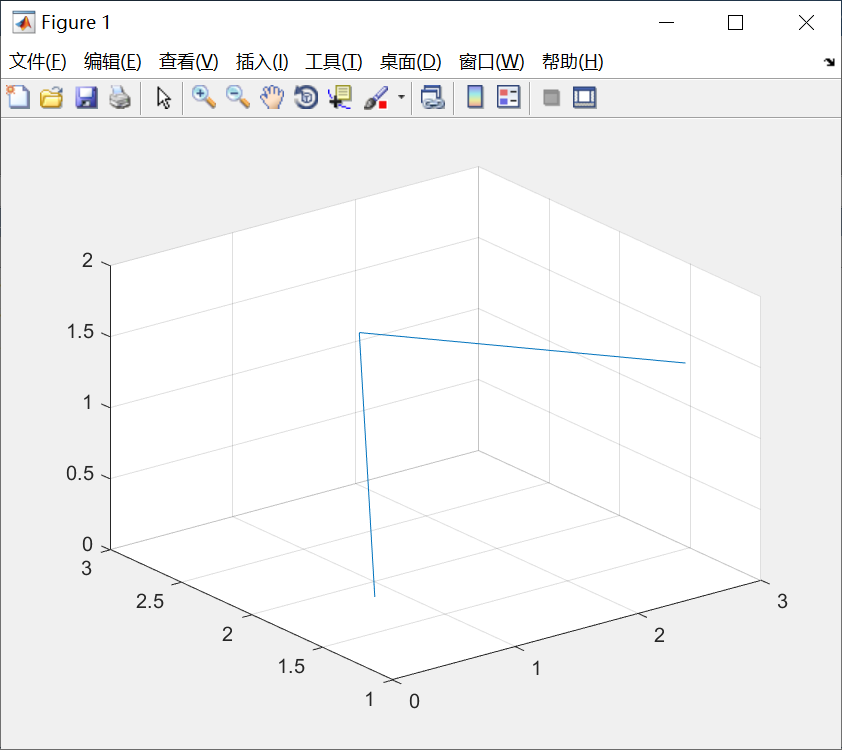
四、三维曲线

 

plot3函数

fplot3函数

 

1.plot3函数

 

plot3函数的基本用法：

plot3（x，y，z）

其中，参数x，y，z组成一组曲线的坐标。通常，x、y、z为长度相同的向量。

 

例子：绘制一条空间折线。

x=[0.2,1.8,2.5];
y=[1.3,2.8,1.1];
z=[0.4,1.2,1.6];
plot3(x,y,z);
grid on;    //显示网格线
axis([0,3,1,3,0,2]);

图像：

 

例子：

 

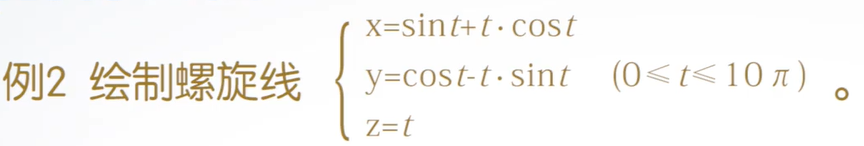
代码：

t = linspace(0,10*pi,200);
x = sin(t) + t.*cos(t);
y = cos(t) + t.*sin(t);
z = t;
subplot(1,2,1);
plot3(x,y,z);
grid on;
subplot(1,2,2);
plot3(x(1:4:200),y(1:4:200),z(1:4:200));
grid on;

曲线：

 

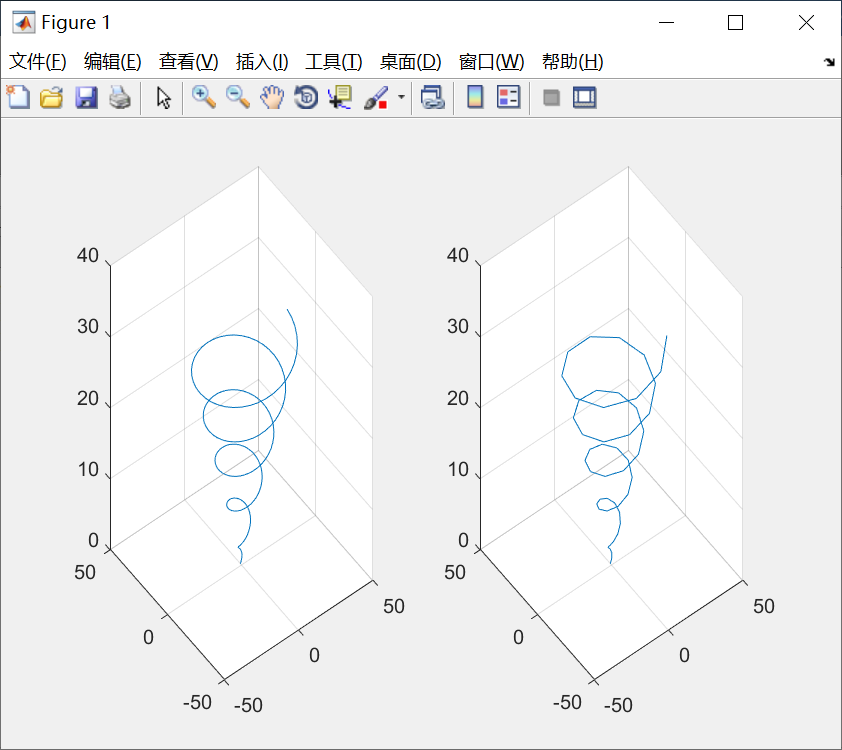
plot3函数参数的变化形式

 

plot3（x，y，z）

参数x、y、z是同型矩阵时，则以xyz对列元素绘制曲线。曲线条数等于矩阵列数。

当参数xyz中既有向量，也有矩阵时，向量的长度应该与矩阵相符。也就是说，行向量的长度与矩阵的列数相同，列向量的行数与矩阵的列数相同。

 

例子：

在空间不同位置绘制5条正弦曲线。

代码：

t = 0:0.01:2*pi;
t = t';
x = [t,t,t,t,t];
y = [sin(t),sin(t) + 1,sin(t)+2,sin(t)+3,sin(t)+4];
z=[t,t,t,t,t];
plot3(x,y,z);

代码还可以这样：

其实就是行向量，和列向量的问题。

图像：

 

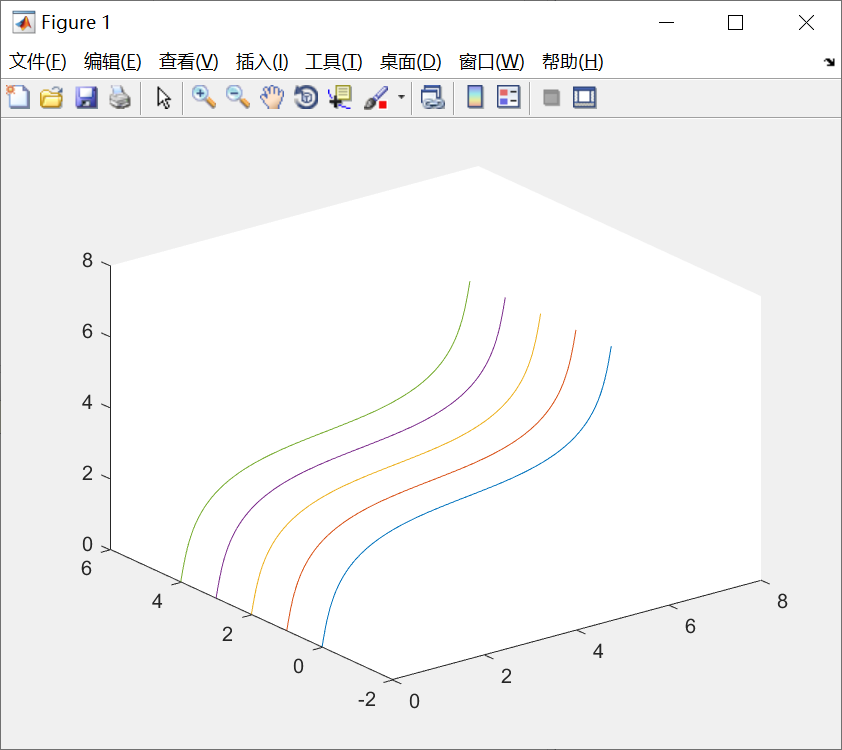
含多组输入参数的plot3函数

 

plot3（x1,y1,z1,x2,y2,z2,```,xn,yn,zn）

每一组x、y、z向量构成一组数据点的坐标，绘制一条曲线。

代码：

t1 = 0:0.01:1.5*pi;
t2 = 0:0.01:2*pi;
t3 = 0:0.01:3*pi;
plot3(t1,sin(t1),t1,t2,sin(t2)+1,t2,t3,sin(t3)+2,t3);

图线：

 

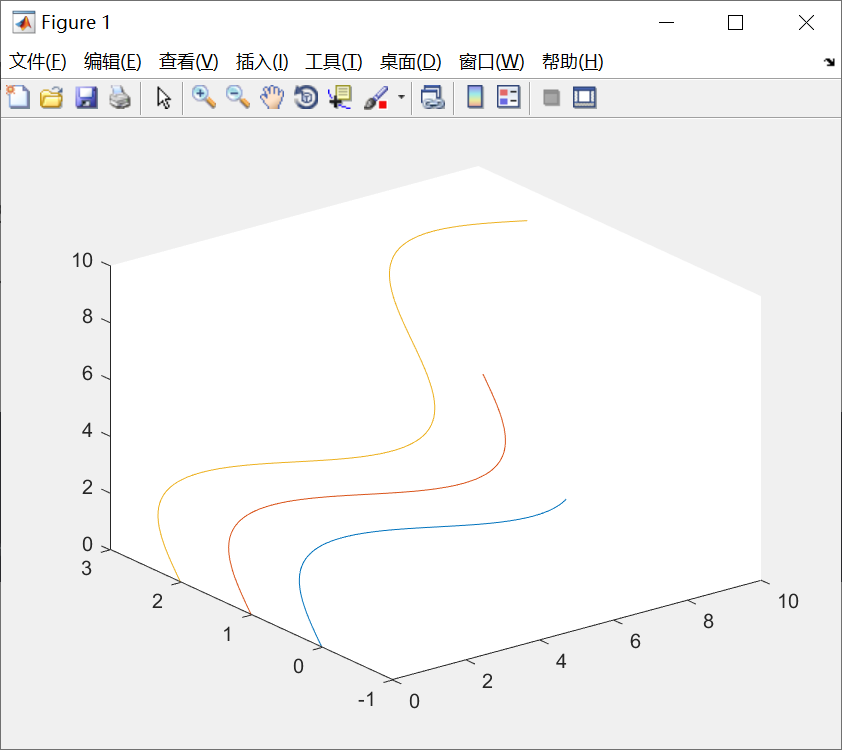
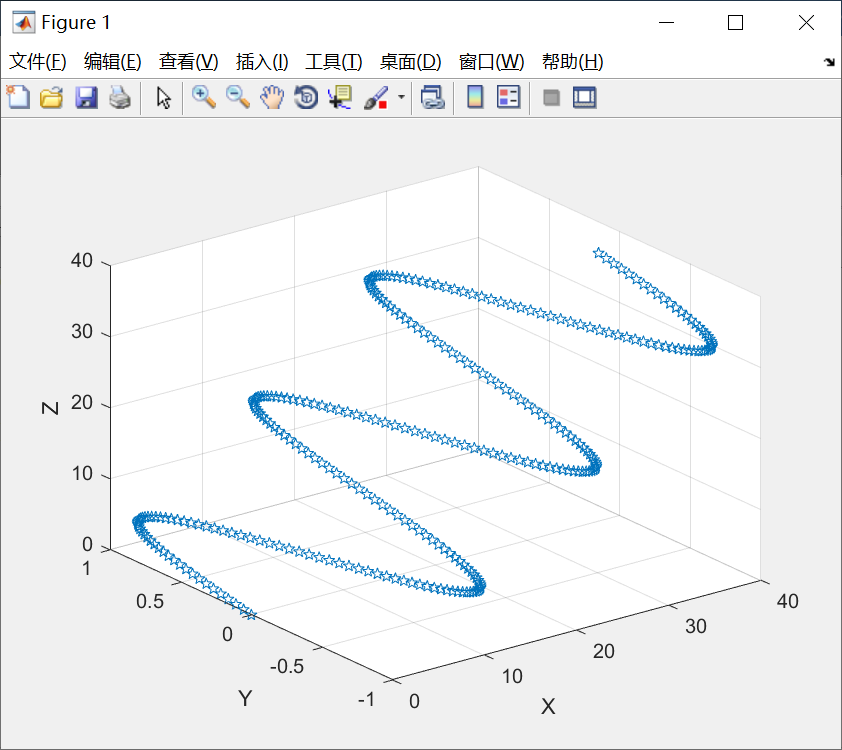
含选项的plot3函数

plot3（x，y，z，选项）

选项用于指定曲线的线型、颜色和数据点标记。

例子：

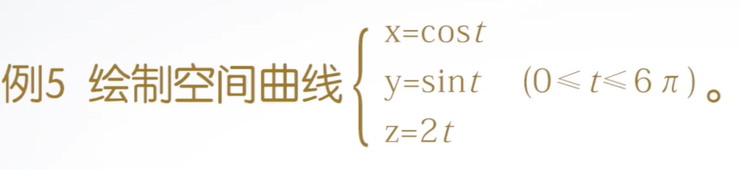
代码：

t = 0:pi/50:6*pi;
x=cos(t);
y=sin(t);
z=2*t;
plot3(z,y,z,'p');
xlabel('X'),ylabel('Y'),zlabel('Z');
grid on;

图线：

 

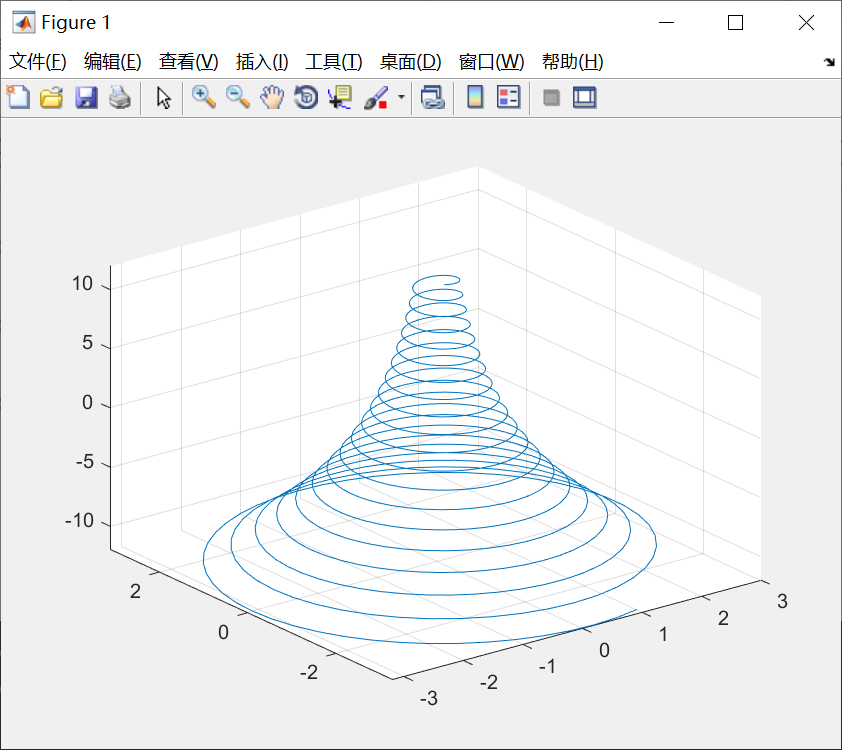
2.fplot3函数

 

fplot3（funx，funy，funz，tlims）

其中，funx、funy、funz代表定义曲线x、y、z坐标的函数，通常采用函数句柄的形式。tlims为参数函数自变量的取值范围，用二元向量[tmin，tmax]描述，默认为[-5,5]。

 

例子：

 

代码：

xt=@(t)exp(-t/10).*sin(5*t);
yt=@(t)exp(-t/10).*cos(5*t);
zt=@(t)t;
fplot3(xt,yt,zt,[-12,12]);

图线：

 

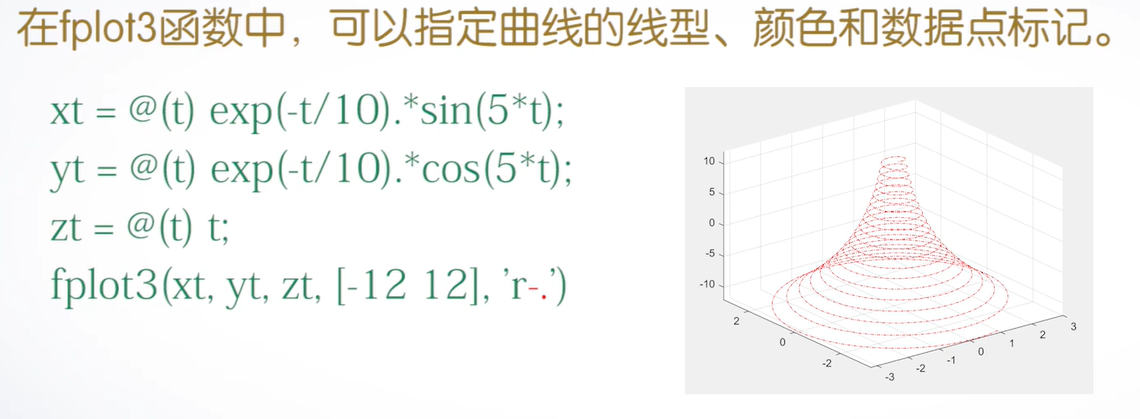
在fplot函数中，可以指定曲线的线型、颜色和数据点标记。

 

五、三维曲面

 

平面网格数据的生成

绘制三维曲面的mesh函数和surf函数

fmesh函数和fsurf函数

 

1.平面网格数据的生成

 

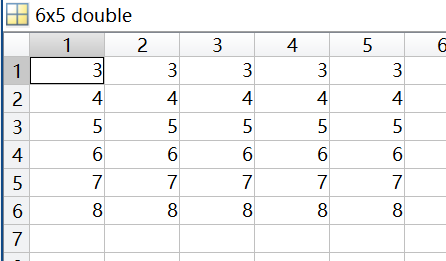
利用矩阵运算生成

x=2:6;
y=(3:8)';
X=ones(size(y))*x;
Y=y*ones(size(x));

生成的数据：

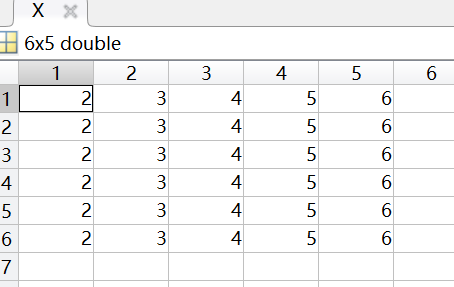
数据

 

利用meshgrid函数生成

 

[X,Y] = meshgrid(x,y);

其中，参数x、y为向量，存储网格点坐标的X、Y为矩阵。

 

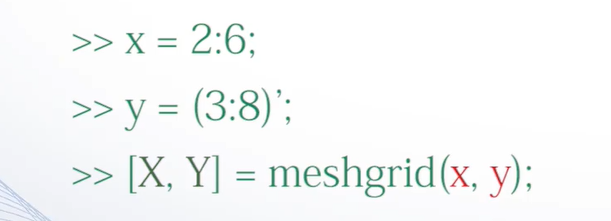
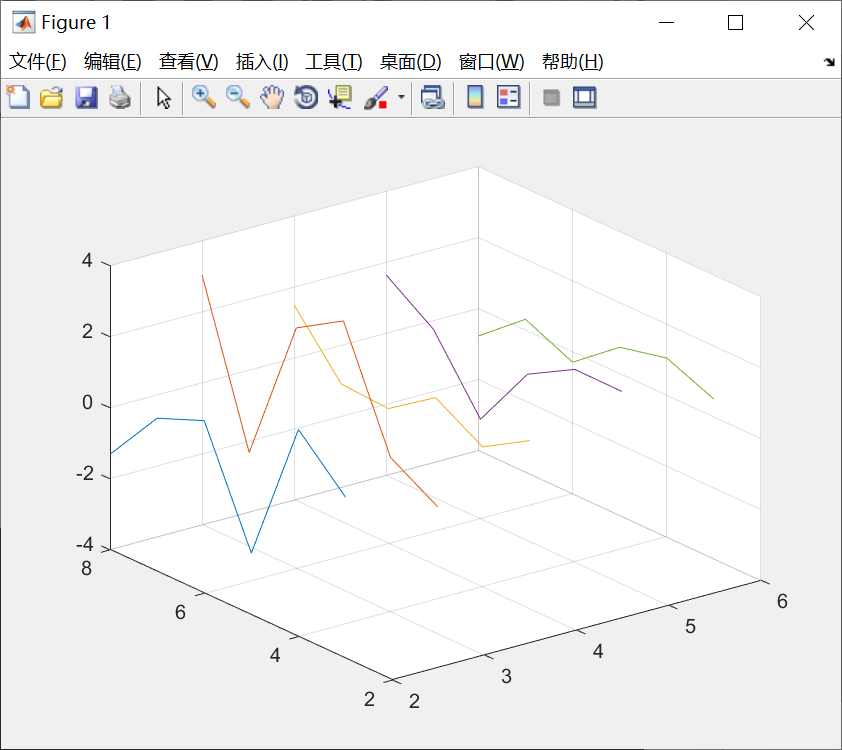
例子：

绘制空间曲线：

代码：

x=2:6;
y=(3:8)';
[X,Y] = meshgrid(x,y);
Z=randn(size(X));
plot3(X,Y,Z);
grid on;

图线：

 

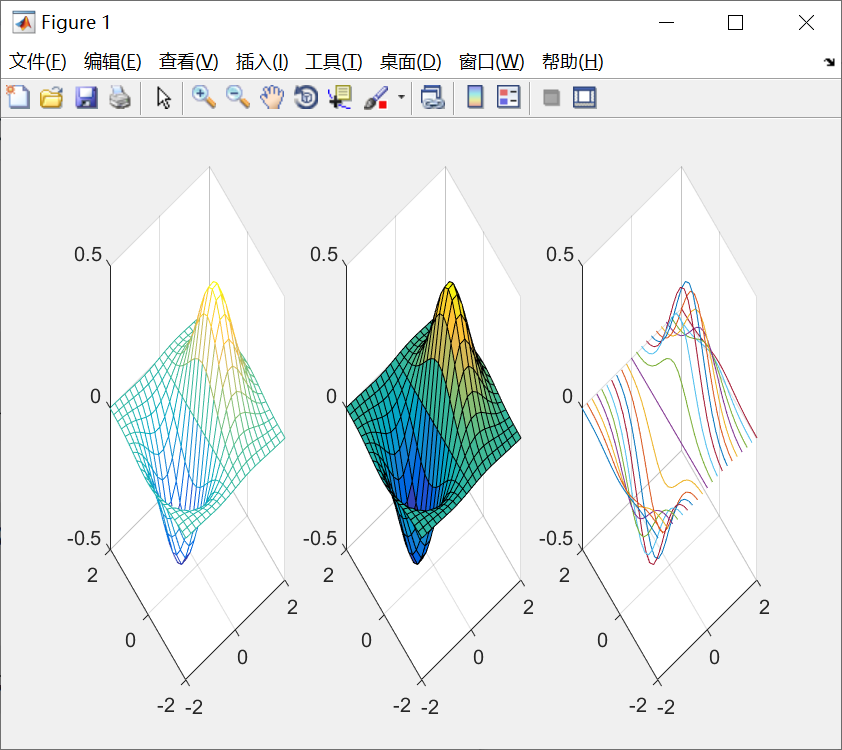
2.绘制三维曲面的函数

 

mesh（x，y，z，c）

surf（x，y，z，c）

其中，x、y是网格坐标矩阵，z是网格点上的高度矩阵，c用于指定在不同高度下的曲面颜色。不给定c是，默认c等于z，也就是图形的颜色是正比于图形的高度的。

例子：

代码：

t = -2:0.2:2;
[X,Y] = meshgrid(t);
Z=X.*exp(-X.^2-Y.^2);
subplot(1,3,1);
mesh(X,Y,Z);
subplot(1,3,2);
surf(X,Y,Z);
subplot(1,3,3);
plot3(X,Y,Z);
grid on;

图线：

 

mesh函数和surf函数的其他调用格式：

mesh（z，c）

surf（z，c）

当x、y省略时，z矩阵的第2维下标当作x轴坐标，z矩阵的第维下标当作y轴坐标。

 

 

• 带等高线的三维网格曲面函数meshc
• 带底座的三维网格曲面函数meshz

 

• 具有等高线的曲面函数surfc
• 具有光照效果的曲面函数surfl

 

例子：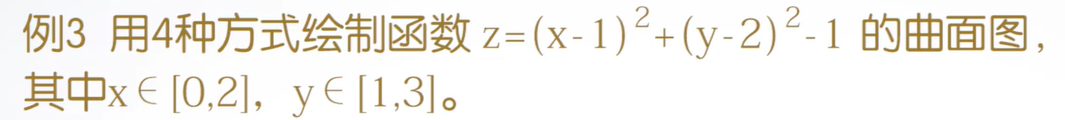

代码：

[x,y]=meshgrid(0:0.1:2,1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1);
meshc(x,y,z);
title('meshc(x,y,z)');
subplot(2,2,2);
meshz(x,y,z);
title('meshz(x,y,z)');
subplot(2,2,3);
surfc(x,y,z);
title('surfc(x,y,z)');
subplot(2,2,4);
surfl(x,y,z);
title('surfl(x,y,z)');

图线：

 

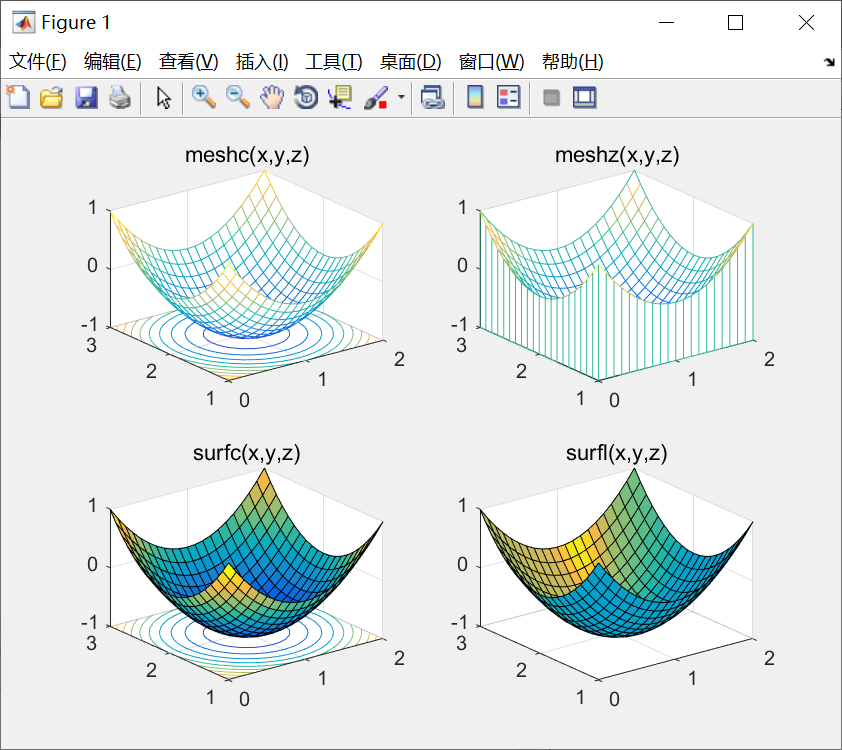
3.标准三维曲面

 

sphere函数

[x,y,z] = sphere(n)   n为球面光滑程度，默认20，n越小，则表面越粗糙

cylinder函数

[x,y,z] = cylinder(R,n)  R为向量，n为间隔点

 

例子：

代码：

subplot(1,3,1);
[x,y,z] = cylinder;
surf(x,y,z);
subplot(1,3,2);
t=linspace(0,2*pi,40);
[x,y,z] = cylinder(2+cos(t),30);
surf(x,y,z);
subplot(1,3,3);
[x,y,z]=cylinder(0:0.2:2,30);
surf(x,y,z);

图形：

 

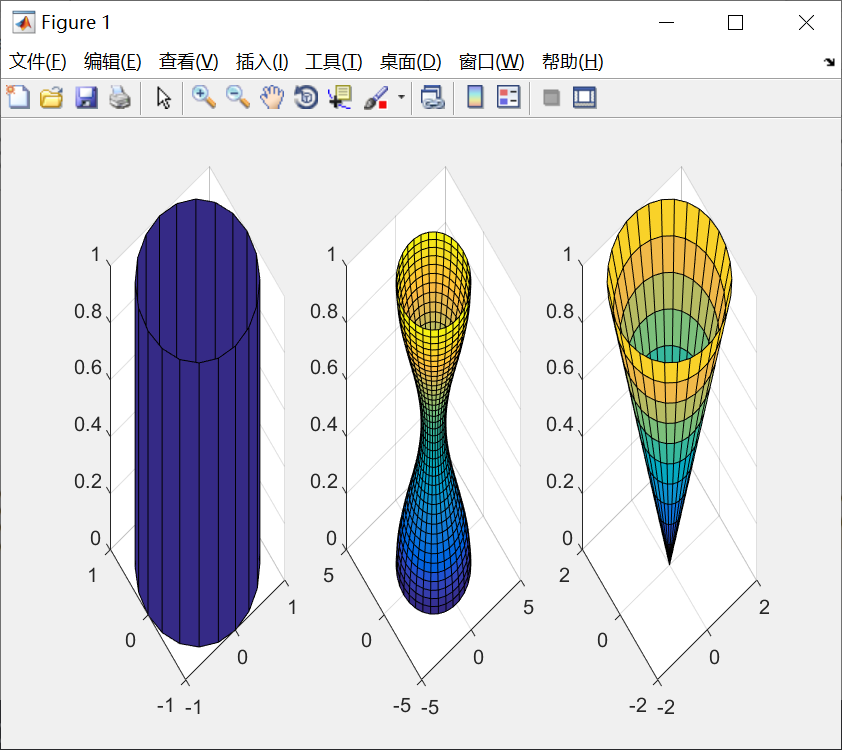
例子：

 

代码：

[x,y,z] = cylinder(1,60);
z=[-1*z(2,:);z(2,:)];
surf(x,y,z);
hold on;    //叠加
surf(y,z,x);
axis equal;  //将横轴纵轴的定标系数bai设成相同值。

图形：

 

peaks函数

 

4.fsuf函数和fmesh函数

如果函数有三个参数方程，由两个参数，则可以使用这两个函数，调用格式如下：

fsurf(funx,funy,funz,uvlims)

fmesh(funx,funy,funz,uvlims)

其中，funx、funy、funz代表定义曲面x、y、z坐标的函数，通常采用函数句柄的形式。uvlims为funx、funy和funz的自变量的取值范围，用4元向量[umin,umax,vmin,vmax]描述，默认为[-5,5,-5,5]。

 

例子：

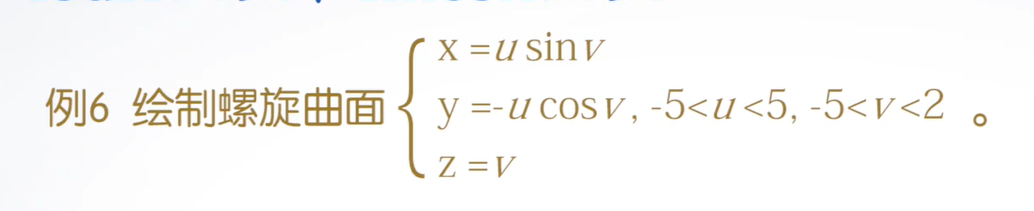
代码：

funx = @(u,v)u.*sin(v);
funy = @(u,v)-u.*cos(v);
funz = @(u,v)v;
fsurf(funx,funy,funz,[-5,5,-5,-2]);
hold on;
fmesh(funx,funy,funz,[-5,5,-2,2]);
hold off;

图线：

 

六、图形修饰处理

 

• 视点处理
• 色彩处理
• 裁剪处理

 

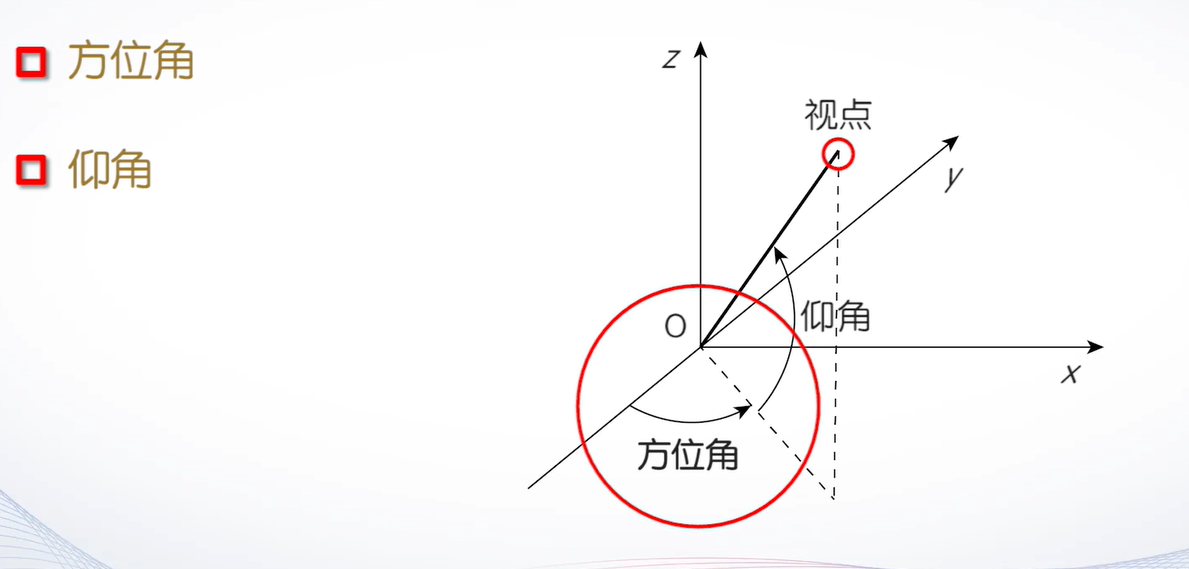
1.视点处理

方位角

仰角

 

 

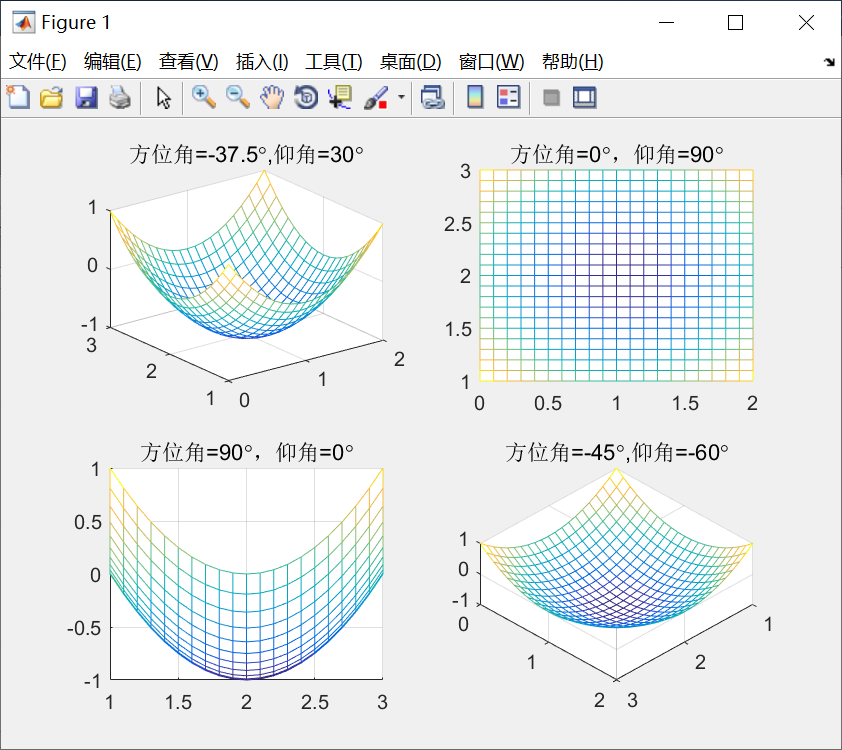
view函数的基本用法

view(az,el)

其中，az为方位角，el为仰角。

 

例子：

代码：

[x,y]=meshgrid(0:0.1:2,1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1);
mesh(x,y,z);
title('方位角=-37.5{circ},仰角=30{circ}');
subplot(2,2,2);
mesh(x,y,z);
view(0,90);
title('方位角=0{circ}，仰角=90{circ}');
subplot(2,2,3);
mesh(x,y,z);
view(90,0);
title('方位角=90{circ}，仰角=0{circ}');
subplot(2,2,4);
mesh(x,y,z);
view(-45,-60);
title('方位角=-45{circ},仰角=-60{circ}');

图线：

 

view函数的其他用法

 

view（x,y,z）

view(2)

view(3)

 

2.色彩处理

 

颜色的向量表示

[R，G，B]

 

色图（Colotmap）

色图矩阵

内建色图

 

 

 

指定当前图形使用的色图

colormap cmapname

colormap（cmap）

 

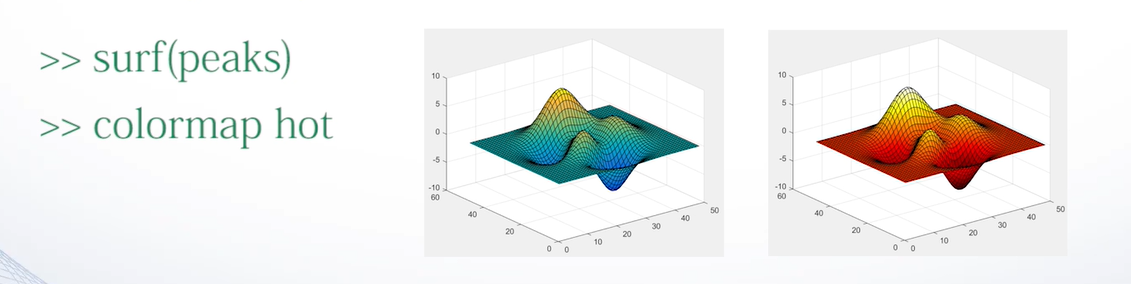
• 创建色图矩阵

色图矩阵的每一行是RGB三元组。可以自定义色图矩阵，也可以调用MATLAB提供的函数来定义色图矩阵。

例子：

创建一个灰色系列色图矩阵。

c=[0,0.2,0.4,0.6,0.8,1]';
cmap = [c,c,c];
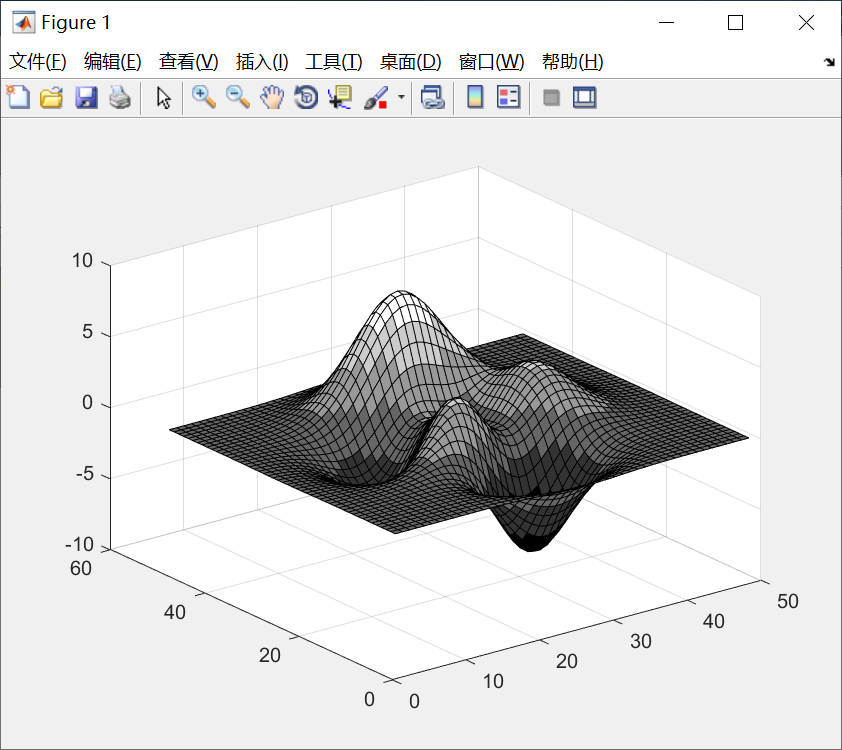
surf(peaks);
colormap(cmap);

图线：

 

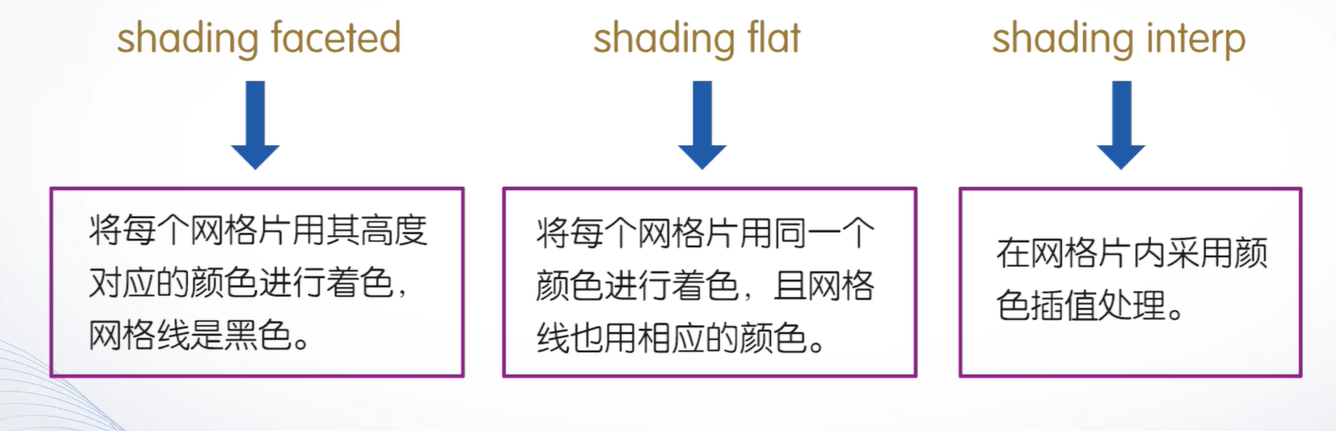
三维图形表面的着色

 

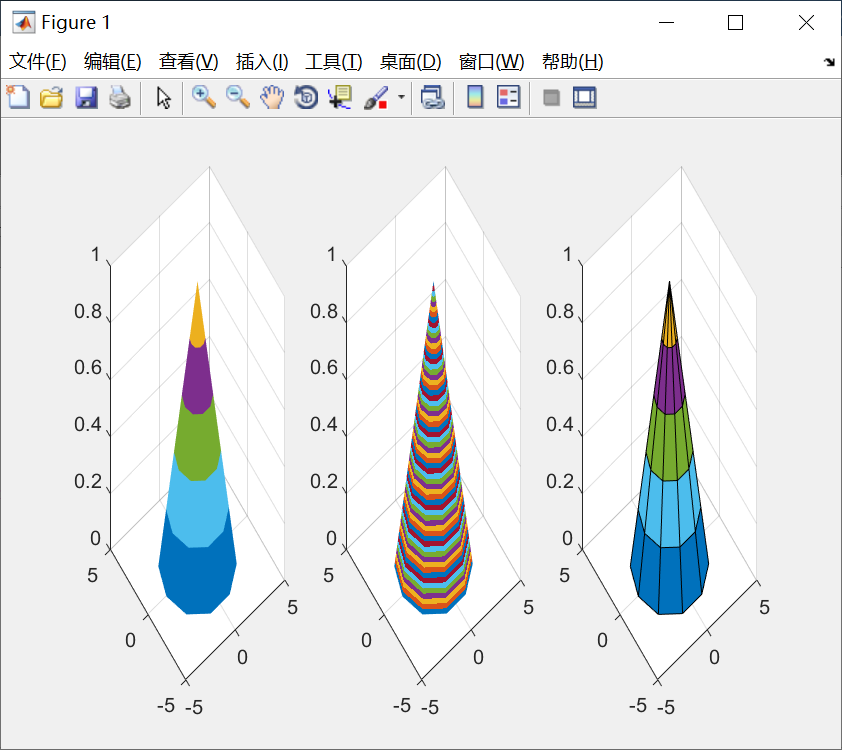
例子：使用同一色图，以不同着色方式绘制圆锥体。

[x,y,z] = cylinder(pi:-pi/5:0,10);
colormap(lines);
subplot(1,3,1);
surf(x,y,z);
shading flat;
subplot(1,3,2);
surf(x,y,z);
shading interp;
subplot(1,3,3);
surf(x,y,z);

图线：

 

3.图形的裁剪处理

将图形中需要裁剪部分对应的函数值设置成NaN，这样在绘制图形时，函数值为NaN的部分将不显示出来，从而达到对图形进行裁剪的目的。

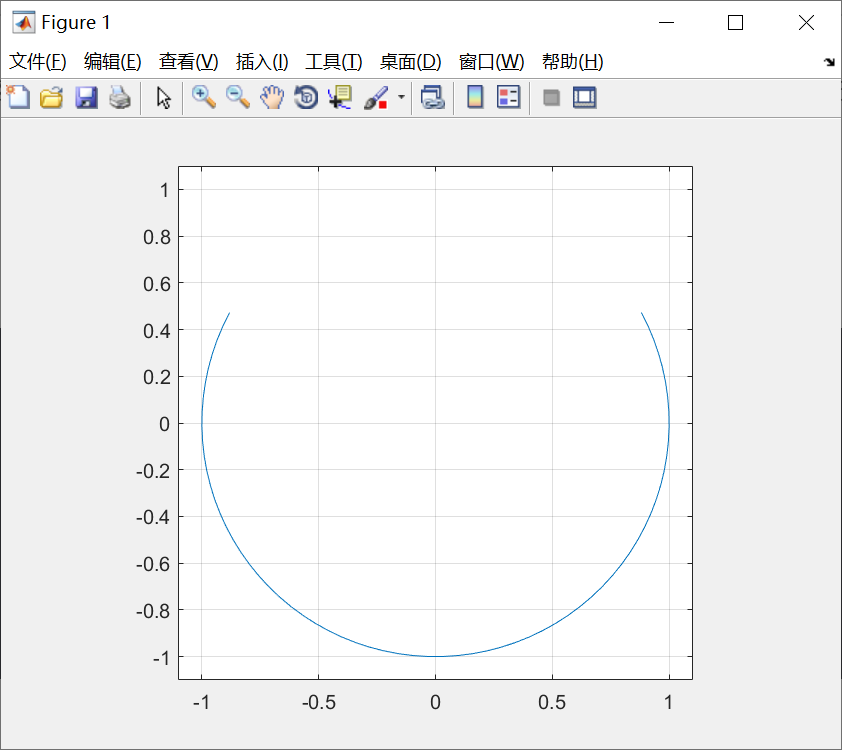
例子：绘制3/4圆。

代码：

t=linspace(0,2*pi,100);
x = sin(t);
y = cos(t);
p = y > 0.5;
y(p)=NaN;
plot(x,y);
axis([-1.1,1.1,-1.1,1.1]);
axis square;
grid on;

图线：

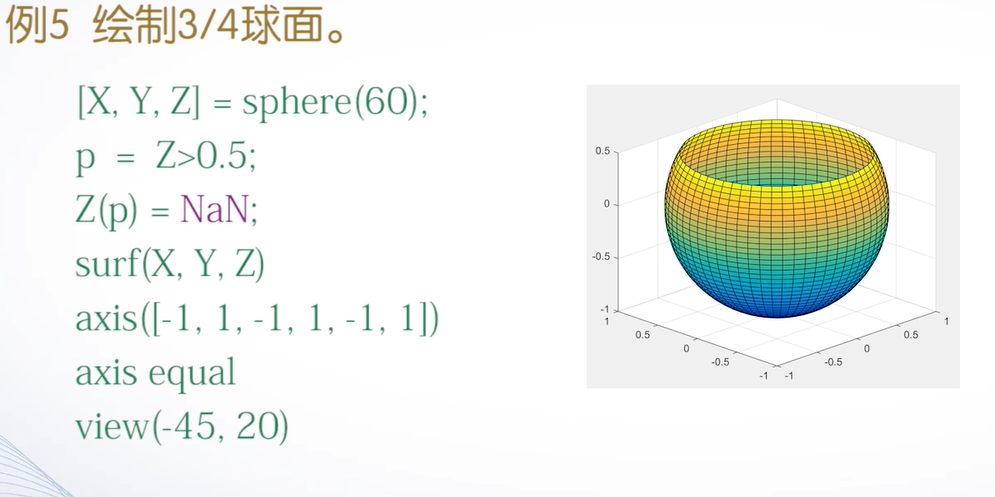
例子：

绘制3/4球面

 

七、交互式绘图工具

 

“绘图”选项卡

图形窗口绘图工具

图形窗口菜单和工具栏

 

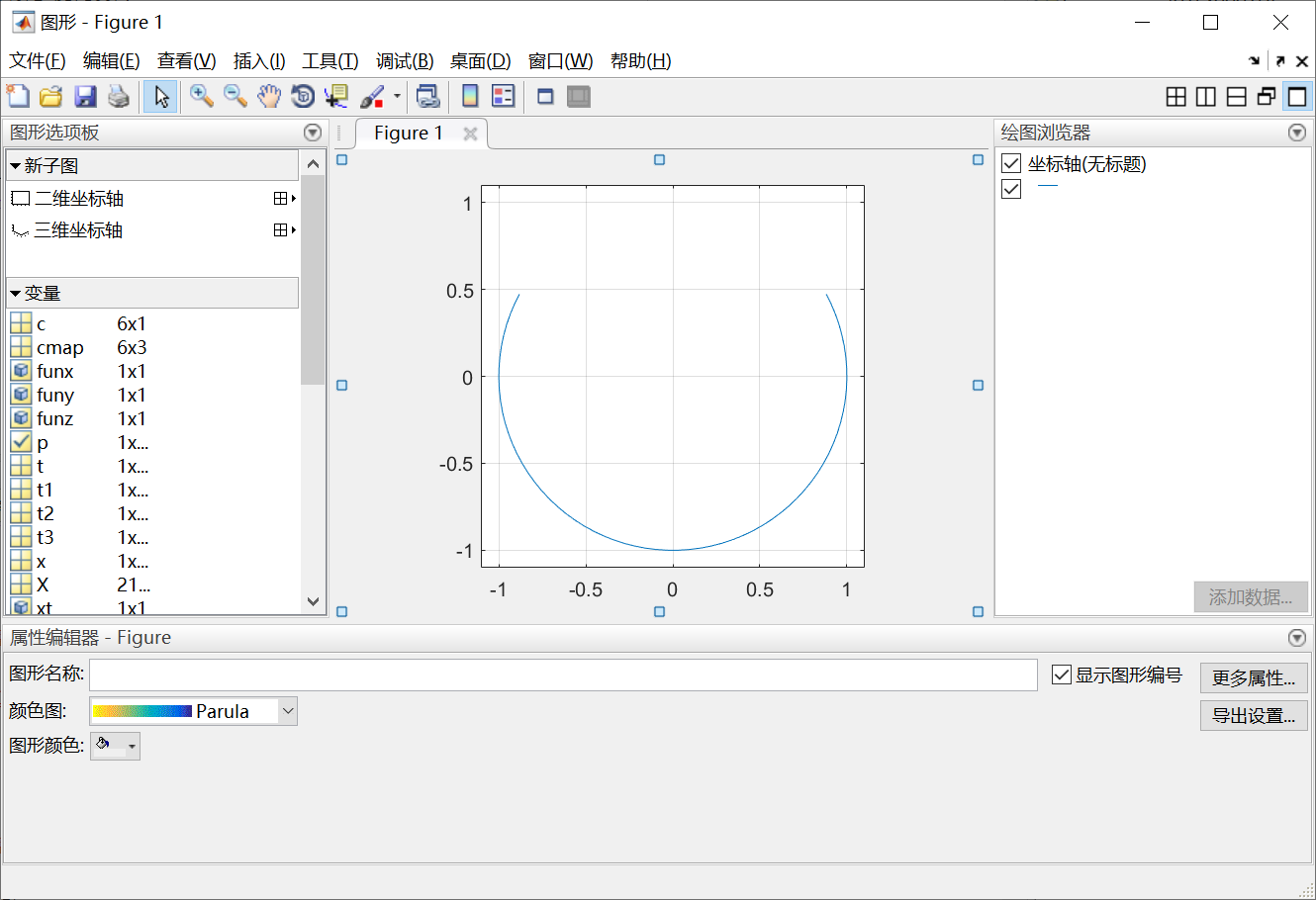
1.“绘图”选项卡

 

一般按照选定的顺序确定xyz的顺序，就是操纵面板里面的选项。

 

显示绘图工具

 

 

绘图工具的组成

 

图形选项板

绘图浏览器

属性编辑器

 

 

小结

 

 

 

 

 

 

 

 

 

最后

以上就是暴躁河马为你收集整理的MATLAB笔记4：MATLAB绘图一、二维曲线二、绘制图形的辅助操作三、其他形式的二维曲线四、三维曲线五、三维曲面六、图形修饰处理七、交互式绘图工具小结的全部内容，希望文章能够帮你解决MATLAB笔记4：MATLAB绘图一、二维曲线二、绘制图形的辅助操作三、其他形式的二维曲线四、三维曲线五、三维曲面六、图形修饰处理七、交互式绘图工具小结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。