数学建模学习GM（1,1）灰色预测模型

1.灰色系统的定义：

灰色系统指既含有已知信息又含有未知信息的系统。

2.灰色预测模型的定义：

对灰色系统进行预测的模型。

灰色模型（Grey Model，简称GM模型）一般表达方式为GM（n,x）模型，其含义是：用n阶微分方程对x个变量建立模型。

3.灰色预测模型的目的：

通过把分散在时间轴上的离散数据看成一组连续变化的序列，采用累加和累减的方式，将灰色系统中的未知因素弱化，强化已知因素的影响程度，最后构建一个以时间为变量的连续微分方程，通过数学方法确定方程中的参数，从而实现预测目的。

4.灰色系统预测模型的特点：

无需大量数据样本，短期预测效果好，运算过程简单。

5.灰色系统预测模型的不足：

对非线性数据样本预测效果差。

常用的灰色系统预测模型主要有GM(1,1)和GM(1,n)，以下分别对这两种模型展开。
【1】.GM(1,1)模型

1. GM（1,1）模型的预测原理是：对某一数据序列用累加的方式生成一组趋势明显的新数据序列，按照新的数据序列的增长趋势建立模型进行预测，然后再用累减的方法进行逆向计算，恢复原始数据序列，进而得到预测结果。
2. GM(1,1)建模过程：
   (1) 设一组原始数据为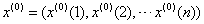，n为数据个数。对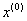累加以便弱化随机序列的波动性和随机性,得到新的数列为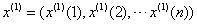：其中，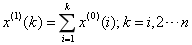
   (2) 生成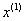的邻均值等权数列 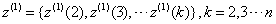其中，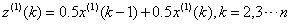
   (3) 根据灰色理论对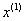 建立关于t的白化形式的一阶一元微分方程GM(1,1):
   
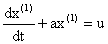
   其中，a，u为待解系数,分别称为发展系数和灰色作用量，a的有效区间是(-2,2)，并记a，u构成的矩阵为灰参数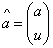 ,只要求出参数a，u，就能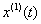求出,进而求出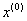的预测值。
   (4) 对累加生成数据做均值生成B与常数项向量 :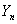
   
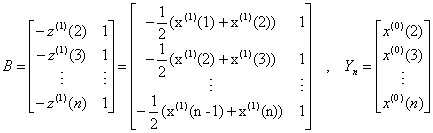
   (5) 用最小二乘法求解灰参数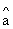,则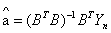
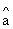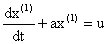   (6) 将灰参数代入，并对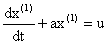 进行求解，得
   
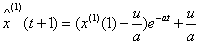
   (7) 将上述结果累减还原，即可得到预测值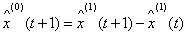
   (8) 利用模型进行预测: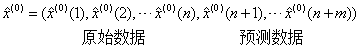
   (9) 对建立的灰色模型进行精度检验,
   (9.1)残差检验：
   残差：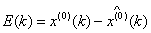
   相对误差：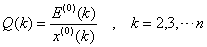
   (9.2)后验差检验：
   均值：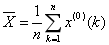
   方差：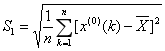
   残差的均值：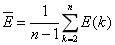
   残差的方差：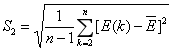
   后验差比值：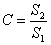
   小误差概率：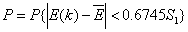
   (9.3) 预测精度等级对照如下：
   预测精度等级
   好 P>0.95 C<0.35
   合格 P>0.80 C<0.45
   勉强合格 P>0.70 C<0.50
   不合格 P<=0.70 C>=0.65

最后

以上就是震动飞鸟为你收集整理的数学建模学习GM（1,1）灰色预测模型的全部内容，希望文章能够帮你解决数学建模学习GM（1,1）灰色预测模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。