灰色预测GM(1,1)代码

1.一项初始序列X0

import numpy as np
import math as mt
import matplotlib.pyplot  as plt
 
X0 = [15,16.1,17.3,18.4,18.7,19.6,19.9,21.3,22.5]

2.累加序列，生成新序列

X1 = [15]
add = X0[0] + X0[1]
X1.append(add)
i = 2
while i < len(X0):
    add = add+X0[i]
    X1.append(add)
    i += 1
print("X1",X1)

X1 [15, 31.1, 48.400000000000006, 66.80000000000001, 85.50000000000001, 105.10000000000002, 125.00000000000003, 146.30000000000004, 168.80000000000004]

3.紧邻均值生成序列

Z = []
j = 1
while j < len(X1):
    num = (X1[j]+X1[j-1])/2
    Z.append(num)
    j = j+1
print("紧邻均值生成序列Z（背景值）：",Z)

紧邻均值生成序列Z（背景值）： [23.05, 39.75, 57.60000000000001, 76.15, 95.30000000000001, 115.05000000000003, 135.65000000000003, 157.55000000000004]

4.求相关参数

#4.1 求Y
Y = []
x_i = 0
while x_i < len(X0)-1 :
    x_i += 1
    Y.append(X0[x_i])
    
Y = np.mat(Y).T#化为矩阵，进行矩阵运算
Y.reshape(-1,1)
print("Y",Y)
 
#4.2 求B
B = []
b = 0
while b < len(Z) :
    B.append(-Z[b])
    b += 1

B = np.mat(B)#数组转矩阵
B.reshape(-1,1)
B = B.T
c = np.ones((len(B),1))#生成len(B)行1列的数组
B = np.hstack((B,c))#合并，水平方向叠加
print("B",B)

Y [[16.1]
[17.3]
[18.4]
[18.7]
[19.6]
[19.9]
[21.3]
[22.5]]
B [[ -23.05 1. ]
[ -39.75 1. ]
[ -57.6 1. ]
[ -76.15 1. ]
[ -95.3 1. ]
[-115.05 1. ]
[-135.65 1. ]
[-157.55 1. ]]

5.由第四步求出参数

theat = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)#最小二乘法:使拟合函数求的值与已知数据的平方差最小
a1 = theat[0][0]#发展系数
b1 = theat[1]#驱动系数
print(theat)
a=float(a1)
b=float(b1)
print("发展系数a:",a)
print("驱动系数b:",b)

[[-0.04352981]
[15.41559771]]
发展系数a: -0.043529807634855366
驱动系数b: 15.41559770935472

6.生成预测模型

F = []
F.append(X0[0])
k = 1
did=b/a
'''
while k < len(X0)+2: #当k<=8时，求的是拟合值；加2意思是预测了未来两年的，即预测值
    F.append((X0[0]-did)*mt.exp(-a*k)+did)
    k += 1
print("预测模型F：",F)
'''
while k < len(X0):
    F.append((X0[0]-did)*mt.exp(-a*k)+did)
    k += 1
print("预测模型F：",F)

（k,g+2）：
预测模型F： [15.0, 31.423405429147238, 48.57750668582446, 66.49481325137344, 85.20928099062075, 104.75637650310938, 125.17314433739045, 146.4982771957536, 168.77218926244535, 192.03709279434298, 216.33707811923313]
(k,g不+2）：
预测模型F： [15, 31.423405429147238, 48.57750668582446, 66.49481325137344, 85.20928099062075, 104.75637650310938, 125.17314433739045, 146.4982771957536, 168.77218926244535]

7.累减还原，得原始数列的灰色预测值

G = []
G.append(X0[0])
g = 1
'''
含预测未来2年
while g<len(X0)+2:
    G.append(F[g]-F[g-1])
    g +=1
print("原始数列的灰色拟合值和未来2年预测值:",G)
'''
while g<len(X0):
    G.append(F[g]-F[g-1])
    g +=1
print("原始数列的灰色拟合值:",G)

/注释中（k,g+2）：
原始数列的灰色拟合值和未来2年预测值: [15, 16.423405429147238, 17.154101256677222, 17.917306565548984, 18.71446773924731, 19.547095512488625, 20.416767834281075, 21.325132858363133, 22.273912066691764, 23.26490353189763, 24.299985324890145]
/非注释中（k,g不+2）：（适用于8模型检验）
原始数列的灰色拟合值: [15.0, 16.423405429147238, 17.154101256677222, 17.917306565548984, 18.71446773924731, 19.547095512488625, 20.416767834281075, 21.325132858363133, 22.273912066691764, 23.26490353189763, 24.299985324890145]

8.模型检验

//注意：针对k和g没有+2时

print("残差检验")
# 8.1残差检验
#8.1.1绝对误差序列
X0 = np.array(X0)
G = np.array(G)
e=abs(X0-G)
print("绝对误差序列:",e)
#8.1.2相对误差序列
q=e/X0
print("相对误差序列:",q)
q_mean=sum(q)/len(q)
print("q_mean=",q_mean)
print()

print("后验差检验")
#8.2 后验差检验
#8.2.1计算原始序列标准差s1（此处计算的是方差，与s2分母相同）
s1 = np.var(X0) # 方差
print("原始序列方差s1:",s1)
#8.2.2计算绝对误差序列的标准差s2(（此处计算的是方差，与s2分母相同）)
s2 = np.var(e)
print("绝对误差序列的方差s2:",s2)
#8.2.3计算方差比
c = s2/s1 
print("方差比:",c)
#8.2.4计算小误差概率P
p=0
for s in range(len(e)):
    if (abs(e[s]) < 0.6745 * s1):
        p = p + 1
P = p/len(e)
print("小误差概率P:",P)

残差检验
绝对误差序列: [0. 0.32340543 0.14589874 0.48269343 0.01446774 0.05290449
0.51676783 0.02513286 0.22608793]
相对误差序列: [0. 0.02008729 0.00843345 0.02623334 0.00077368 0.00269921
0.02596823 0.00117995 0.01004835]
q_mean= 0.010602611361110747

后验差检验
原始序列方差s1: 5.102469135802469
绝对误差序列的方差s2: 0.03619043724355282
方差比: 0.0070927302606527435
小误差概率P: 1.0

9.可视化

r0 = range(9)
t0 = list(r0)
r1 = range(11)
t1 = list(r1)
plt.plot(t0,X0,color='r',linestyle="--",label='true')
plt.plot(t1,G,color='b',linestyle="--",label="predict")
plt.legend(loc='upper right')
plt.show()

k,g+2：

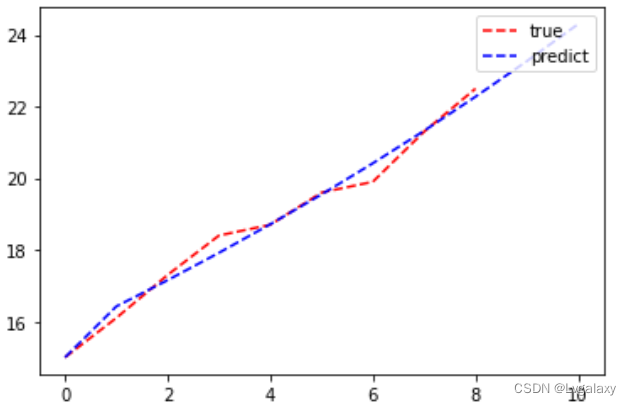
k,g不+2：

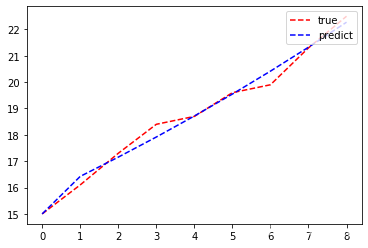
//可见相比前面的原始图像，新的序列和年份的图像看起来像是一条直线！

这就是累加生成制造出来的规律(注意：更常见的是指数形式的图像，本题直线型的图像可视作指数型图像的特例)

结果分析

该GM(1,1)模型的适用范围
由第5步代码结果（发展系数a）得知-a0.04<0.35，所以该GM(1,1)模型可以应用到中长期预测中，且预测效果非常好[6]。
精度检验

• 由第8步中的残差检验结果得知，相对误差序列均值q_mean -0.01，说明该GM(1,)模型为残差优模型。
• 由第8步中的后验差检验结果方差比C0.0071<0.35,且小误差概率P=1.0>0.95，得知该模型预测精度等级为好。

补充：既然有GM(1,1)模型，自然有GM(2,1)、GM(1,2)模型等。其中GM(2,1)就代表利用一个变量的二阶微分方程来进行灰色预测。本题的新序列与年份的函数图像接近指数函数或直线，是单调的变化过程，适合GM(1,1)模型；而如果画出的图像是非单调的摆动序列或饱和的S型序列，则可考虑GM(2,1)模型。

最后

以上就是故意小刺猬为你收集整理的灰色预测GM(1,1)代码的全部内容，希望文章能够帮你解决灰色预测GM(1,1)代码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。