数学建模：灰色预测模型GM(1,1)matlab实现

灰色预测的主要特点是模型使用的不是原始数据序列，而是生成的数据序列。其核
心体系是灰色模型(GreyModel,GM)，即对原始数据作累加生成(或其他方法生成)得到
近似的指数规律再进行建模的方法。优点是不需要很多的数据,一般只需要4个数据，就
能解决历史数据少、序列的完整性及可靠性低的问题；能利用微分方程来充分挖掘系统的
本质,精度高；能将无规律的原始数据进行生成得到规律性较强的生成序列，运算简便，易
于检验，不考虑分布规律，不考虑变化趋势。缺点是只适用于中短期的预测，只适合指数
增长的预测。

GM(1,1)预测模型

GM(1,1)模型预测步骤

1)数据的检验与处理

$$\begin{gathered} 首先，为了保证建模方法的可行性，需要对已知数据列作必要的检验处理。设参考数据为 \\ {x}^{(0)}=(x^{(0)}(1),x^{(0)}(2),...,x^{(0)}(n))，计算序列的级比 \end{gathered}$$
$$\lambda (k)=\frac{x^{(0)}(k-1)}{x(0)(k)},k=2,3,...n。$$
$$\begin{gathered} 如果所有的级比\lambda (k)都落在可容覆盖\Theta =(e^{\frac{-2}{n+1}},e^{\frac{2}{n+2}})内,可以作为模型GM(1,1)的数据进行 \\ 灰色预测。否则，需要对序列x^{(0)}做必要的变换处理，使其落入可容覆盖内。即取适当的常数 \\ c，作平移变换 \end{gathered}$$
$$\begin{gathered} y^{(0)}(k)=y^{(0)}(k)+c,k=1,2,...,n, \\ 使序列y^{(0)}=(y^{(0)}(1),y^{(0)}(2),...,y^{(0)}(n))的级比 \end{gathered}$$
$${\lambda }_y(k)=\frac{y^{(0)}(k-1)}{y(0)(k)}\in \Theta ,k=2,3,...n$$
2)建立模型
预测值

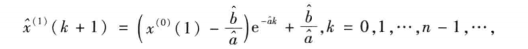
3)检验预测值
$$\begin{gathered} (1)残差检验。令残差为ϵ(k),计算 \\ ϵ(k)=\frac{x^{(0)}(k)-{\hat{x}}^{(0)}(k)}{x^{(0)}(k)},k=1,2,...,n \end{gathered}$$
$$\begin{gathered} 这里{\hat{x}}^{(0)}(1)=x^{(0)}(1),如果ϵ(k)<0.2,则认为达到一般要求;如果ϵ(k)<0.1， \\ 则认为达到较高的要求。 \end{gathered}$$
$$\begin{gathered} 级比偏差值检验。首先由参考数据:x^{(0)}(k-1)，x^{(0)}(k)计算出级比\lambda (k)，再用发展系数a \\ 求出相应的级比偏差 \\ \rho (k)=1-\frac{1-0.5a}{1+0.5a}\lambda (k) \\ 如果\rho (k)<0.2，则可认为达到一般要求；如果\rho (k)<0.1，则认为达到较高要求 \end{gathered}$$
4)预测预报
由CM(1,1)模型得到指定时区内的预测值,根据实际问题的需要,给出相应的预测
预报。

城市交通噪声数据

附上matlab代码

clc, clear
x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6]';%注意这里为列向量
n=length(x0);
lamda =x0(1:n-1)./x0(2:n)%计算级比
range = minmax( lamda') %计算级比的范围
x1 = cumsum(x0)%累加运算
B=[ -0.5*(x1(1:n-1) +x1(2:n)),ones(n-1,1)];
Y = x0(2:n);
u=BY%拟合参数u(1) =a,u(2) =b
syms x(t)
x= dsolve(diff(x) +u(1) *x==u(2),x(0)==x0(1)); %求微分方程的符号解
xt=vpa(x,6)%以小数格式显示微分方程的解
yucel =subs(x,t,[0:n-1]); %求已知数据的预测值
yucel = double(yucel);%符号数转换成数值类型,否则无法做差分运算.
yuce=[ x0(1),diff(yucel)]%差分运算,还原数据
epsilon=x0'-yuce%计算残差
delta = abs( epsilon./x0')%计算相对误差
rho=1-(1 -0.5*u(1))/(1 +0.5*u(1)) * lamda'%计算级比偏差值,u(1) =a
n=7;
t1=1:n;
t2=1:n;
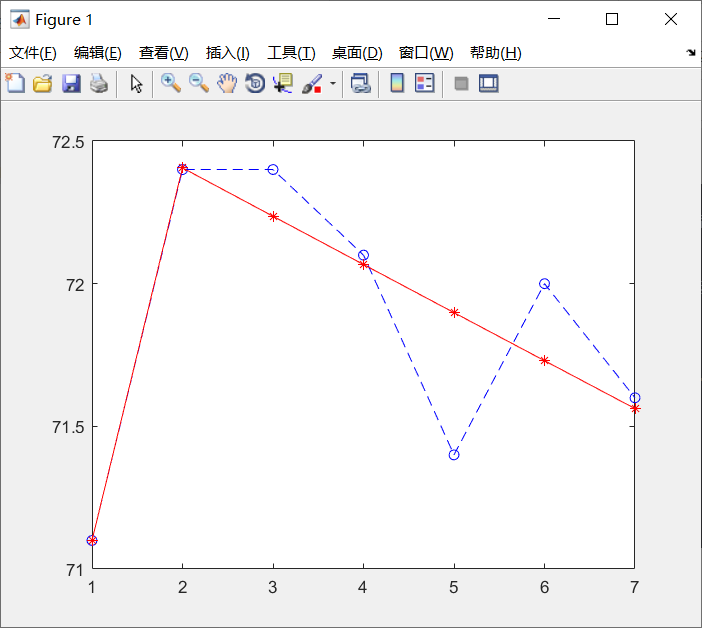
plot(t1,x0,'bo--');
hold on;
plot(t2,yuce,'r*-'); 

lamda =
    0.9820
    1.0000
    1.0042
    1.0098
    0.9917
    1.0056
range =
    0.9820    1.0098
x1 =
   71.1000
  143.5000
  215.9000
  288.0000
  359.4000
  431.4000
  503.0000
u =
    0.0023
   72.6573
xt =
31000.0 - 30928.9*exp(-0.00234379*t)
yuce =
   71.1000   72.4057   72.2362   72.0671   71.8984   71.7301   71.5622
epsilon =
         0   -0.0057    0.1638    0.0329   -0.4984    0.2699    0.0378
delta =
         0    0.0001    0.0023    0.0005    0.0070    0.0037    0.0005
rho =
    0.0203    0.0023   -0.0018   -0.0074    0.0107   -0.0032
>> 

转载请标明出处，谢谢！。

如果感觉本文对您有帮助，请留下您的赞，您的支持是我坚持写作最大的动力，谢谢！

最后

以上就是专一月光为你收集整理的数学建模：灰色预测模型GM(1,1)matlab实现的全部内容，希望文章能够帮你解决数学建模：灰色预测模型GM(1,1)matlab实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。