前言

PID控制器在工业界应用非常广泛，但是PID的参数调节一般需要人工根据经验法来试。对于有经验的工程师来说，一般试几次就可以获得满足调节的参数。然而对于新手工程师却很难确定一套比较好的参数。

这里我们采用强化学习的方法来调节PID参数。

这个例子展示了如何使用双延迟深度确定性策略梯度(TD3：twin-delayed deep deterministic policy gradient)强化学习算法来调整PI控制器。整定控制器的性能与使用Control System Tuner app整定的控制器的性能进行了比较。在SIMULINK中使用Control System Tuner app来整定控制器需要Simulink Control Design软件。

对于具有少量可调参数的相对简单的控制任务，基于模型的整定技术与基于无模型的RL方法相比，具有更快的整定过程，可以获得较好的结果。然而，RL方法更适合于高度非线性系统或自适应控制器整定。

为了便于控制器比较，两种整定方法都使用线性二次型高斯(LQG)目标函数。

此示例使用强化学习(RL) agent来计算PI控制器的增益。并使用神经网络控制器替换PI控制器。

环境模型

环境模型是water tank模型，该控制系统的目标是保持水箱中的水位与参考值相匹配。

打开模型

open_system('watertankLQG');

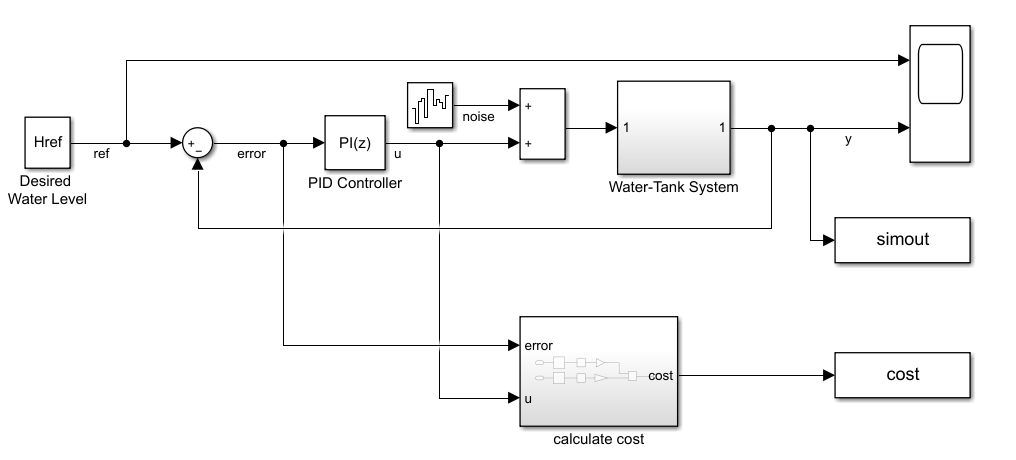
该模型考虑了具有方差$E\left(n^2\left(t\right)\right)=1$的过程噪声。

为了在保持水位的同时最大限度地减少控制力u，本例中的控制器使用以下LQG标准。

$J=\underset{T\Rightarrow \infty }{\lim }E\left(\frac{1}{T}{\int }_0^T\left({\left(\mathrm{r}\mathrm{e}\mathrm{f}-y\right)}^2\left(t\right)+0.01u^2\left(t\right)\right)\mathrm{d}\mathrm{t}\right)$

要在此模型中模拟控制器，必须以秒为单位指定模拟时间Tf和控制器采样时间Ts。

Ts = 0.1;
Tf = 10;

利用控制系统调节器整定PI控制器

要使用Control System Tuner(控制系统整定器)在Simulink中调整控制器，必须将控制器块指定为调整块，并定义调整过程的目标。

在本例中，使用Control System Tuner打开保存的会话ControlSystemTunerSession.mat。本例子将WatertankLQG模型中的PID控制器块指定为调整块，并包含一个LQG整定目标。

controlSystemTuner("ControlSystemTunerSession")

在Tuning条上，点击Tune，来整定控制器。

分别把比例和微分参数调到9.8和1e-6

Kp_CST = 9.80199999804512;
Ki_CST = 1.00019996230706e-06;

创建环境以训练agent

定义模型来训练强化学习的agent，并改进water tank模型，需要以下步骤：

1. 除去PID控制器
2. 加入强化学习agent的模块
3. 创建观测向量${\left[\begin{array}{ccc}\int e\mathrm{d}\mathrm{t}& e& \end{array}\right]}^T$，$e=r-h$，$h$是水箱的高度，$r$是参考高度。把观测信号和强化学习agent模块连接起来。
4. 定义强化学习的回报函数为LQG cost的负值，即 $\mathrm{R}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}=-\left({\left(\mathrm{r}\mathrm{e}\mathrm{f}-h\right)}^2\left(t\right)+0.01u^2\left(t\right)\right)$。强化学习的agent最大化回报，即是最小化LQG cost。

符合上述描述的模型是 rlwatertankPIDTune.slx。

mdl = 'rlwatertankPIDTune';
open_system(mdl)

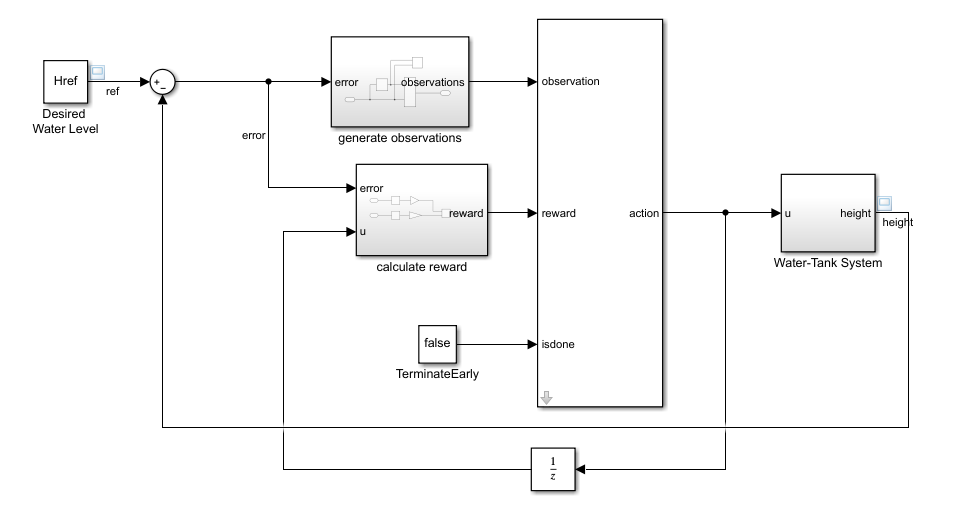
创建环境接口对象。为此，请使用本例末尾定义的localCreatePIDEnv函数：

[env,obsInfo,actInfo] = localCreatePIDEnv(mdl);

输出环境的观测量和动作量的维度值：

numObservations = obsInfo.Dimension(1);
numActions = prod(actInfo.Dimension);

修复随机种子以保证结果复现：

rng(0)

创建TD3 agent

给定观察结果，TD3 agent决定使用参与者表示采取哪个操作。要创建执行元，首先使用观察输入和动作输出创建深度神经网络。

可以将PI控制器建模为具有一个具有误差和误差积分观测的完全连接层的神经网络。
$$u=\left[\begin{array}{ccc}\int e\mathrm{d}\mathrm{t}& e& \end{array}\right]\ast {\left[\begin{array}{ccc}{K}_i& K_p& \end{array}\right]}^T$$
注：

• u 是actor neural network的输出
• $Kp$和$Ki$神经网络权重的绝对值
• $e=r-h$，$h$是水箱的高度，$r$是水箱的参考高度

梯度下降优化可以使权值变为负值。若要避免负权重，可以将普通的fullyConnectedLayer替换为fullyConnectedPILayer。

initialGain = single([1e-3 2]);
actorNetwork = [
    featureInputLayer(numObservations,'Normalization','none','Name','state')
    fullyConnectedPILayer(initialGain, 'Action')];
actorOptions = rlRepresentationOptions('LearnRate',1e-3,'GradientThreshold',1);
actor = rlDeterministicActorRepresentation(actorNetwork,obsInfo,actInfo,...
    'Observation',{'state'},'Action',{'Action'},actorOptions);

TD3 agent使用两个批评值函数表示来近似给定观察和行动的长期奖励。要创建批评者，首先创建一个具有两个输入(观察和动作)和一个输出的深度神经网络。
要创建批评者，请使用本例末尾定义的localCreateCriticNetwork函数。对这两种批评表示使用相同的网络结构。

criticNetwork = localCreateCriticNetwork(numObservations,numActions);
criticOpts = rlRepresentationOptions('LearnRate',1e-3,'GradientThreshold',1);

critic1 = rlQValueRepresentation(criticNetwork,obsInfo,actInfo,...
    'Observation','state','Action','action',criticOpts);
critic2 = rlQValueRepresentation(criticNetwork,obsInfo,actInfo,...
    'Observation','state','Action','action',criticOpts);
critic = [critic1 critic2];

使用以下选项配置agent：

1. 设置agent使用控制器的取样时间Ts
2. 设置mini-batch大小为128
3. 设置经验buffer长度为1e6
4. 将exploration model和目标策略平滑模型设置为使用方差为0.1的高斯噪声。

使用rlTD3AgentOptions指定TD3 agent选项:

agentOpts = rlTD3AgentOptions(...
    'SampleTime',Ts,...
    'MiniBatchSize',128, ...
    'ExperienceBufferLength',1e6);
agentOpts.ExplorationModel.Variance = 0.1;
agentOpts.TargetPolicySmoothModel.Variance = 0.1;

使用指定的actor representation、critic repesention和agent创建TD3 agent：

agent = rlTD3Agent(actor,critic,agentOpts);

训练agent

要训练agent，首先指定以下训练条件：

1. 每个训练的episode最多1000个，每个episode最多100个时间步长。
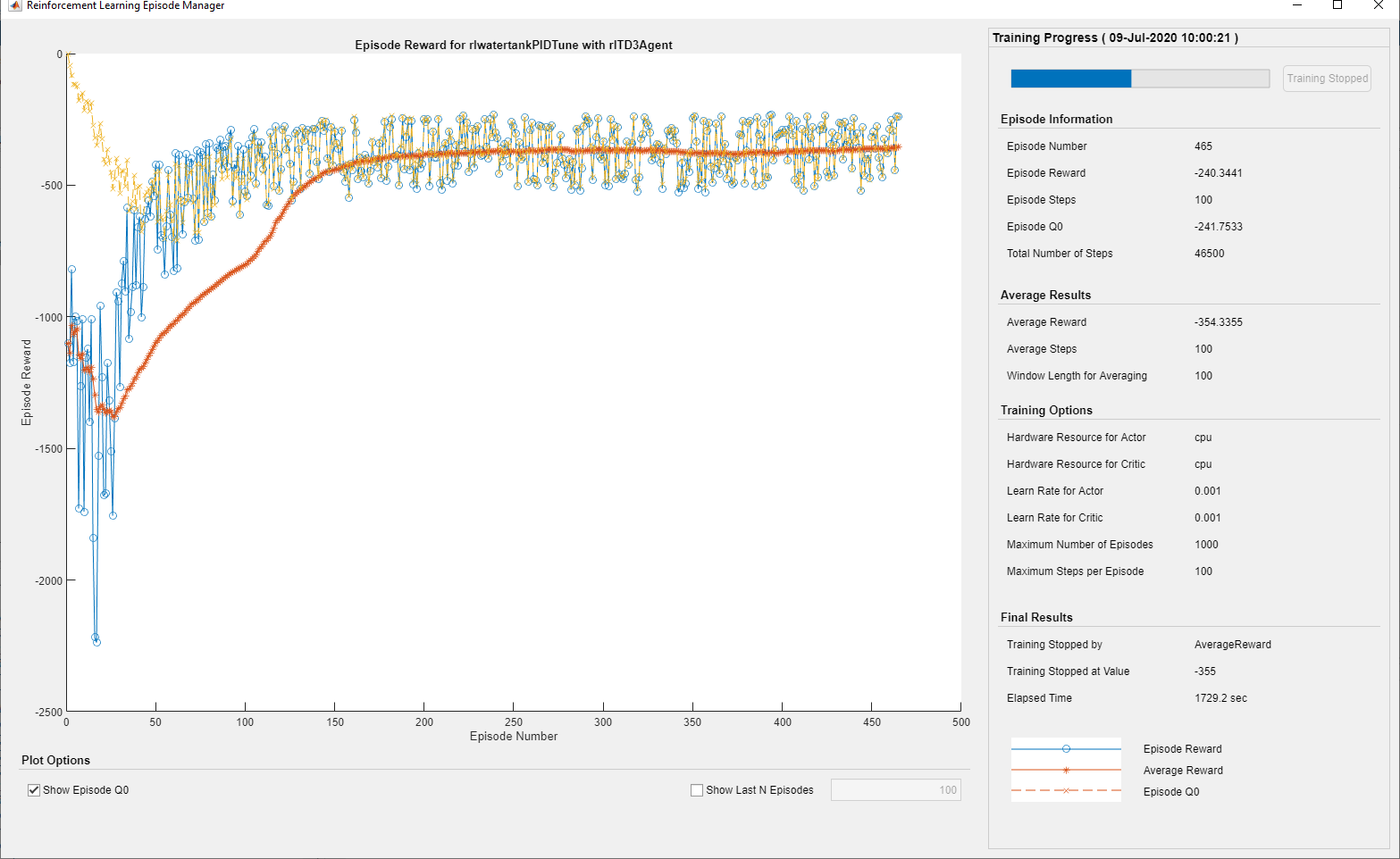
2. 在Episode Manager中显示训练进度(设置Plots选项)，并禁用命令行显示(设置Verbose选项)。
3. 当agent在连续100个episode中获得的平均累计奖励大于-355时，停止训练。则可以认为agent可以控制水箱中的水位。

maxepisodes = 1000;
maxsteps = ceil(Tf/Ts);
trainOpts = rlTrainingOptions(...
    'MaxEpisodes',maxepisodes, ...
    'MaxStepsPerEpisode',maxsteps, ...
    'ScoreAveragingWindowLength',100, ...
    'Verbose',false, ...
    'Plots','training-progress',...
    'StopTrainingCriteria','AverageReward',...
    'StopTrainingValue',-355);

使用train函数训练agent是一个计算量很大的过程，需要几分钟才能完成。要在运行此例子时节省时间，可以通过将doTraining设置为false来加载预先训练的agent。要自己训练agent，请将doTraining设置为true。

if doTraining
    % Train the agent.
    trainingStats = train(agent,env,trainOpts);
else
    % Load pretrained agent for the example.
    load('WaterTankPIDtd3.mat','agent')
end

验证训练好的Agent

通过仿真验证学习到的Agent与模型的一致性：

simOpts = rlSimulationOptions('MaxSteps',maxsteps);
experiences = sim(env,agent,simOpts);

PI控制器的积分和比例增益是执行器表示的绝对值权重。要获得权重，首先从actor中提取可学习的参数。

actor = getActor(agent);
parameters = getLearnableParameters(actor);

获得控制器增益:

Ki = abs(parameters{1}(1));
Kp = abs(parameters{1}(2));

将从RL agent中获得的增益应用于原始PI控制块，并运行阶跃响应仿真。

mdlTest = 'watertankLQG';
open_system(mdlTest);
set_param([mdlTest '/PID Controller'],'P',num2str(Kp))
set_param([mdlTest '/PID Controller'],'I',num2str(Ki))
sim(mdlTest)

提取用于仿真的阶跃响应信息、LQG cost和稳定裕度：

rlStep = simout;
rlCost = cost;
rlStabilityMargin = localStabilityAnalysis(mdlTest);

将使用控制系统调节器获得的增益应用于原始PI控制块，并运行阶跃响应仿真：

set_param([mdlTest '/PID Controller'],'P',num2str(Kp_CST))
set_param([mdlTest '/PID Controller'],'I',num2str(Ki_CST))
sim(mdlTest)
cstStep = simout;
cstCost = cost;
cstStabilityMargin = localStabilityAnalysis(mdlTest);

比较控制器的控制效果

绘制各系统的阶跃响应：

figure
plot(cstStep)
hold on
plot(rlStep)
grid on
legend('Control System Tuner','RL','Location','southeast')
title('Step Response')

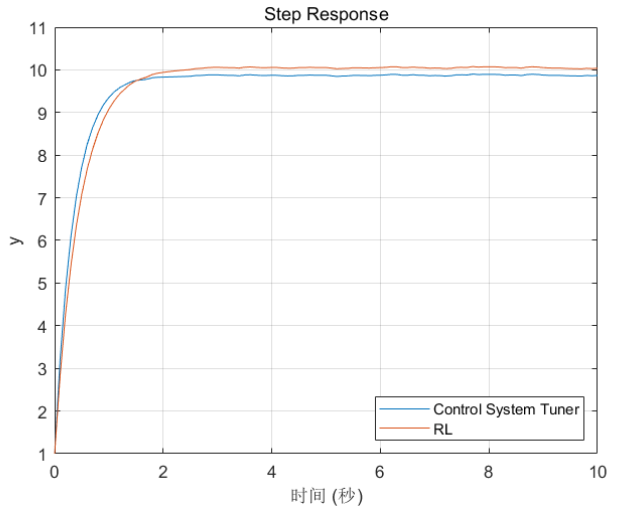
分析两个系统的阶跃响应仿真结果：

rlStepInfo = stepinfo(rlStep.Data,rlStep.Time);
cstStepInfo = stepinfo(cstStep.Data,cstStep.Time);
stepInfoTable = struct2table([cstStepInfo rlStepInfo]);
stepInfoTable = removevars(stepInfoTable,{...
    'SettlingMin','SettlingMax','Undershoot','PeakTime'});
stepInfoTable.Properties.RowNames = {'Control System Tuner','RL'};
stepInfoTable

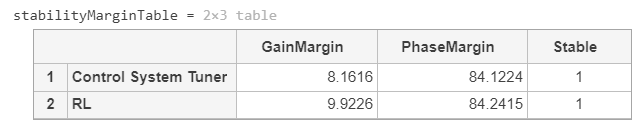
分析两个仿真结果的稳定性：

stabilityMarginTable = struct2table([cstStabilityMargin rlStabilityMargin]);
stabilityMarginTable = removevars(stabilityMarginTable,{...
    'GMFrequency','PMFrequency','DelayMargin','DMFrequency'});
stabilityMarginTable.Properties.RowNames = {'Control System Tuner','RL'};
stabilityMarginTable

比较两个控制器的累积LQG cost。RL调整的控制器产生稍微更优的解决方案。

rlCumulativeCost  = sum(rlCost.Data)

得到：rlCumulativeCost=-375.9135

cstCumulativeCost = sum(cstCost.Data)

cstCumulativeCost=-376.9373

两个控制器都会产生稳定的响应，控制器使用Control System Tuner进行调整会产生更快的响应。然而，RL整定方法产生更高的增益容限和更优化的解决方案。

一些函数的定义

创建water tank强化学习agent的函数：

function [env,obsInfo,actInfo] = localCreatePIDEnv(mdl)

% Define the observation specification obsInfo and action specification actInfo.
obsInfo = rlNumericSpec([2 1]);
obsInfo.Name = 'observations';
obsInfo.Description = 'integrated error and error';

actInfo = rlNumericSpec([1 1]);
actInfo.Name = 'PID output';

% Build the environment interface object.
env = rlSimulinkEnv(mdl,[mdl '/RL Agent'],obsInfo,actInfo);

% Set a cutom reset function that randomizes the reference values for the model.
env.ResetFcn = @(in)localResetFcn(in,mdl);
end

在每个episode开始时随机化参考信号和水箱的初始高度：

function in = localResetFcn(in,mdl)

% randomize reference signal
blk = sprintf([mdl '/Desired nWater Level']);
hRef = 10 + 4*(rand-0.5);
in = setBlockParameter(in,blk,'Value',num2str(hRef));

% randomize initial height
hInit = 0;
blk = [mdl '/Water-Tank System/H'];
in = setBlockParameter(in,blk,'InitialCondition',num2str(hInit));

end

用于线性化和计算SISO水箱系统的稳定裕度的函数：

function margin = localStabilityAnalysis(mdl)

io(1) = linio([mdl '/Sum1'],1,'input');
io(2) = linio([mdl '/Water-Tank System'],1,'openoutput');
op = operpoint(mdl);
op.Time = 5;
linsys = linearize(mdl,io,op);

margin = allmargin(linsys);
end

创建critic网络的函数：

function criticNetwork = localCreateCriticNetwork(numObservations,numActions)
statePath = [
    featureInputLayer(numObservations,'Normalization','none','Name','state')
    fullyConnectedLayer(32,'Name','fc1')];
actionPath = [
    featureInputLayer(numActions,'Normalization','none','Name','action')
    fullyConnectedLayer(32,'Name','fc2')];
commonPath = [
    concatenationLayer(1,2,'Name','concat')
    reluLayer('Name','reluBody1')
    fullyConnectedLayer(32,'Name','fcBody')
    reluLayer('Name','reluBody2')
    fullyConnectedLayer(1,'Name','qvalue')];

criticNetwork = layerGraph();
criticNetwork = addLayers(criticNetwork,statePath);
criticNetwork = addLayers(criticNetwork,actionPath);
criticNetwork = addLayers(criticNetwork,commonPath);

criticNetwork = connectLayers(criticNetwork,'fc1','concat/in1');
criticNetwork = connectLayers(criticNetwork,'fc2','concat/in2');
end

最后

以上就是大胆康乃馨为你收集整理的基于强化学习方法的PID参数整定前言环境模型利用控制系统调节器整定PI控制器创建环境以训练agent训练agent比较控制器的控制效果一些函数的定义的全部内容，希望文章能够帮你解决基于强化学习方法的PID参数整定前言环境模型利用控制系统调节器整定PI控制器创建环境以训练agent训练agent比较控制器的控制效果一些函数的定义所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。