4.1模糊逻辑控制

一种采用模糊集合理论的控制技术，

将模糊数学应用于控制系统，也是一种非线性的智能控制系统。

采用IF条件判断语句和THEN结果语句的方式呈现，其中条件判断语句是利用人的常识判断对控制对象进行控制。

因此，所谓的模糊逻辑控制就是利用人的知识能力，模糊的进行系统控制的方法。

4.2控制系统的架构

4.2.1变量的定义

       定义模糊化变量的函数：

FIS <<-addVar (FIS, varType, varName, varBounds)

FIS：模糊推论系统的名称，必须提供

varType：变量类型，必须指定是输入input还是输出output

varName：完整的变量名称

varBounds：变量值域区间，如：1：10

4.2.2输入与输出模糊化

模糊化输出一般采用最小法则

在R中可定义多种隶属函数，以便将变量模糊化

函数：高斯gaussMF/ 梯形trapMF/ 三角形triMF ( mfName, x, mfParams )

mfName：隶属函数名称字符串

x：隶属函数矢量区间

mfParams：若为gaussMF，输入的参数必须是三个数值的矢量，

其中c（1.5，0，1）中的三个数字代表标准差、平均数和最大值。

例：

Input1:

MF1=gaussMF(“low”,0,c(1.5,0,1))              [low/middle/high]

MF2…

MF3…

Input2:

MF4=trapMF(“few”,0:10,c(0,0,1,3,1))         [few/many]

MF5…

Output1:

MF6=triMF(“middle”,0:30,c(10,15,20,1))    [low/middle/high]

MF7…

MF8…

4.2.3逻辑知识库

又称模糊规则库，一般形式为“IF…and…then…”

在R中可定义模糊规则库，函数为addRule

例：FIS=addRule(FIS,c(3,1,1,1,2))

3，1，1分别代表input1中的MF3，input2的MF5，output1的MF6

第四个数代表权重，一般设定为1，

第五个数代表1=AND,2=OR

4.2.4逻辑判断

模仿人类采用模糊的概念进行判断，

应用之前的模糊规则库和模糊推理得到模糊逻辑控制结果信号

4.2.5解模糊

将推论结果的模糊值转化为明确的控制信号数值，

函数：evalFIS(data,FIS)

data:推论结果的模糊值

FIS：模糊推论系统名称

4.3实例-对教学质量的评价：

注意，这里强调的是数据分析，这些数据怎么来的此处不做解释。

 

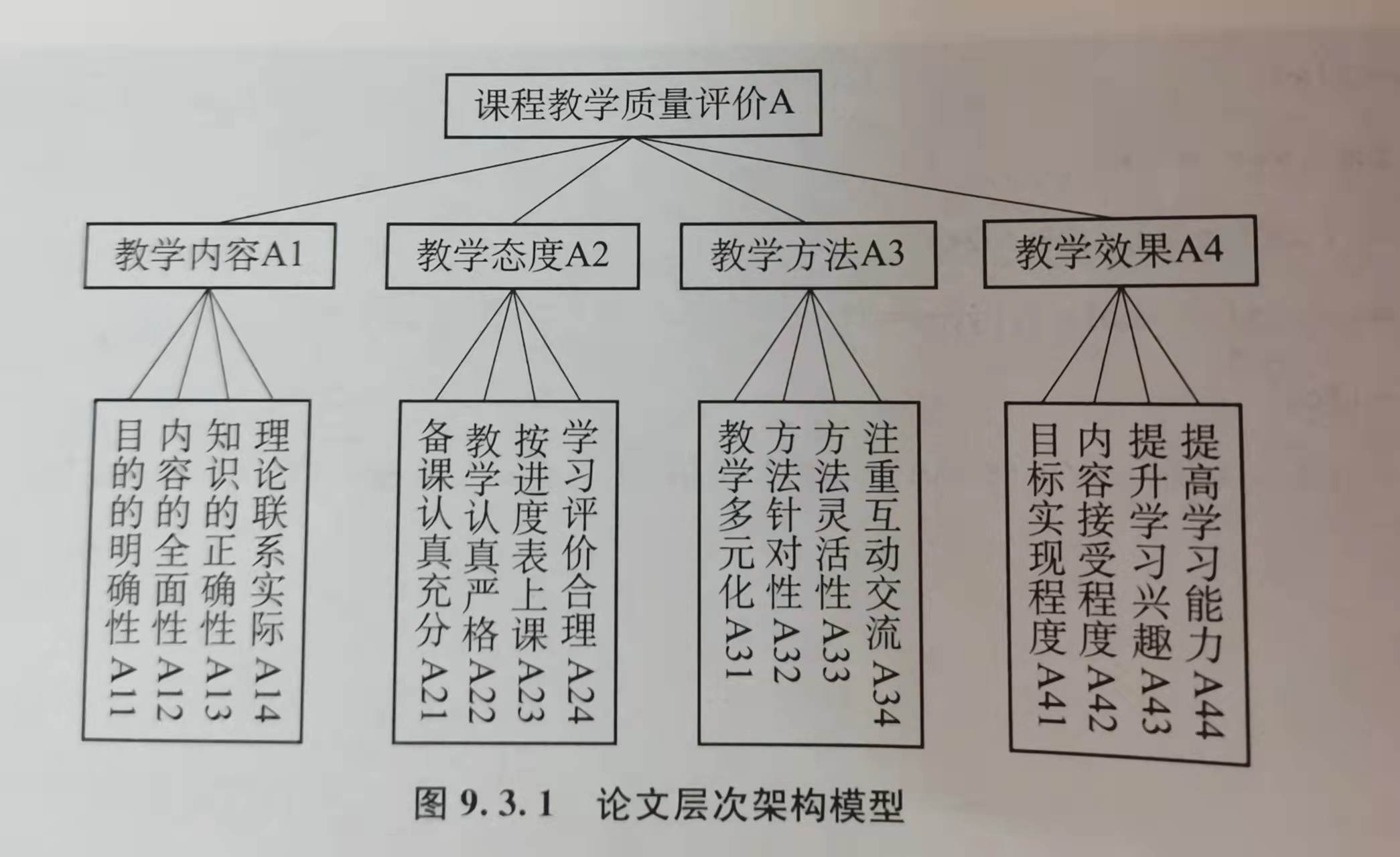
代码：

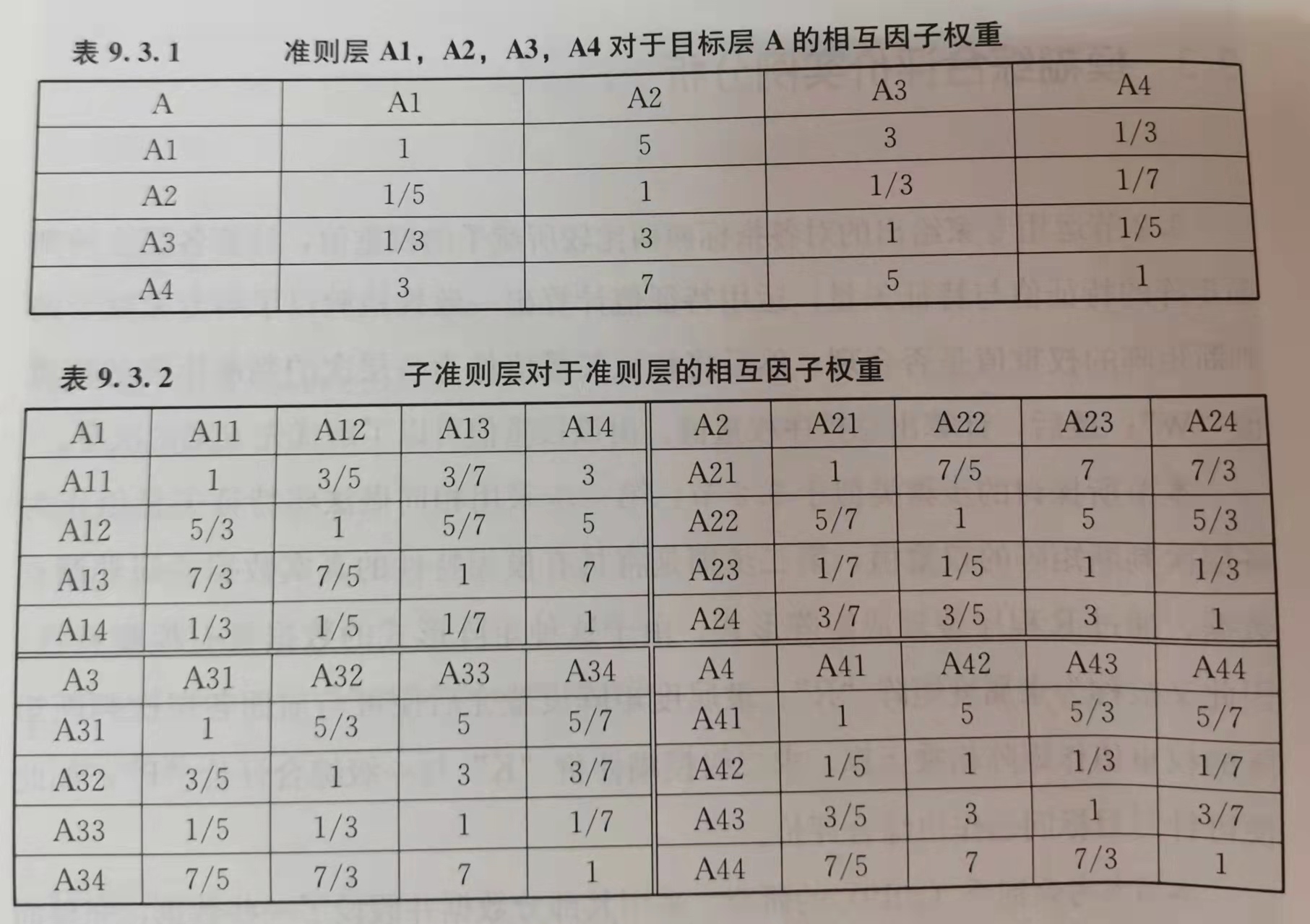
#求出各层次判断矩阵的权重值

#专家判断矩阵目标层

a=c(1,5,3,1/3, 1/5,1,1/3,1/7, 1/3,3,1,1/5, 3,7,5,1)

a=matrix(a, ncol=4, byrow=T)

ev=eigen(a)

lamda=ev$values[1]                        #取出数组第一个值

cil=(lamda-4)/3                                

crl=cil/0.9

w1=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层1 教学内容

b1=c(1,3/5,3/7,3, 5/3,1,5/7,5, 7/3,7/5,1,7, 1/3,1/5,1/7,1)

b1=matrix(b1, ncol=4, byrow=T)

ev=eigen(b1)

lamda=ev$values[1]

ci21=(lamda-4)/3

cr21=ci21/0.9

cr21

w21=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层2 教学态度

b2=c(1,7/5,7,7/3, 5/7,1,5,5/3, 1/7,1/5,1,1/3, 3/7,3/5,3,1)

b2=matrix(b2, ncol=4, byrow=T)

ev=eigen(b2)

lamda=ev$values[1]

ci22=(lamda-4)/3

cr22=ci22/0.9

cr22

w22=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层3 教学方法

b3=c(1,5/3,5,5/7, 3/5,1,3,3/7, 1/5,1/3,1,1/7, 7/5,7/3,7/1,1)

b3=matrix(b3, ncol=4, byrow=T)

ev=eigen(b3)

lamda=ev$values[1]

ci23=(lamda-4)/3

cr23=ci23/0.9

cr23

w23=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层4 教学效果

b4=c(1,5,5/3,5/7, 1/5,1,1/3,1/7, 3/5,3/1,1,3/7, 7/5,7,7/3,1)

b4=matrix(b4, ncol=4, byrow=T)

ev=eigen(b4)

lamda=ev$values[1]

ci24=(lamda-4)/3

cr24=ci24/0.9

cr24

w24=ev$vectors[,1]/sum(ev$vectors[,1])

----------以上代码若有不懂的，请移步本人的另一篇文章《R语言-层次分析法--AHP》-------

 -----------------以下数据仍是需要自己调查计算出来的-----------------

 

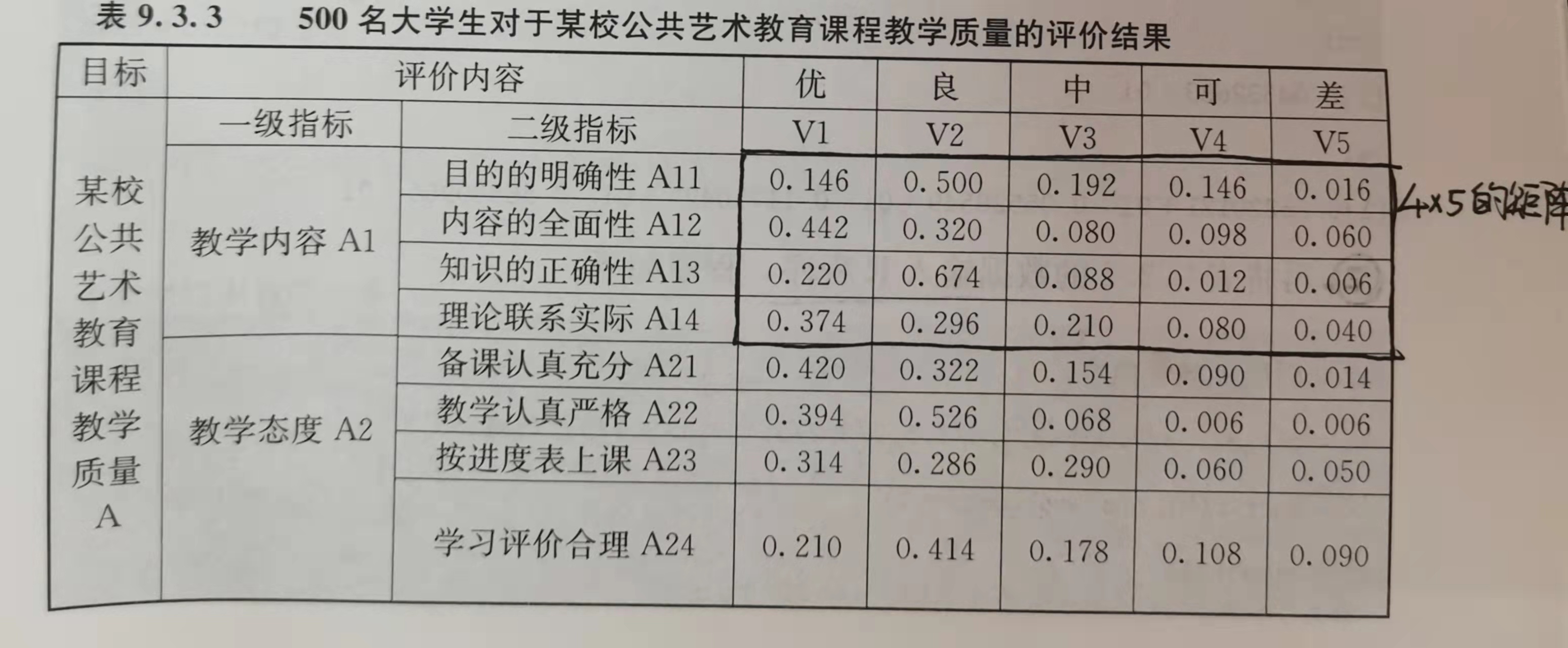
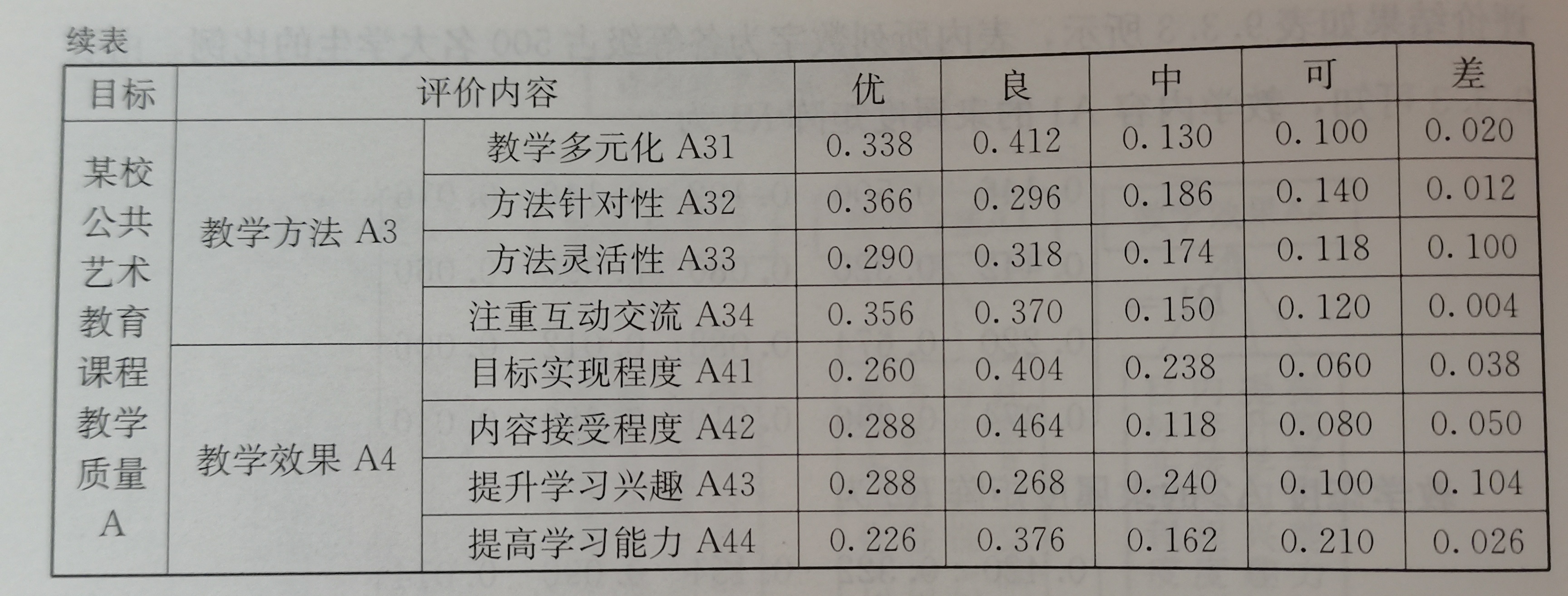
由上面的表格得到下面的矩阵。 

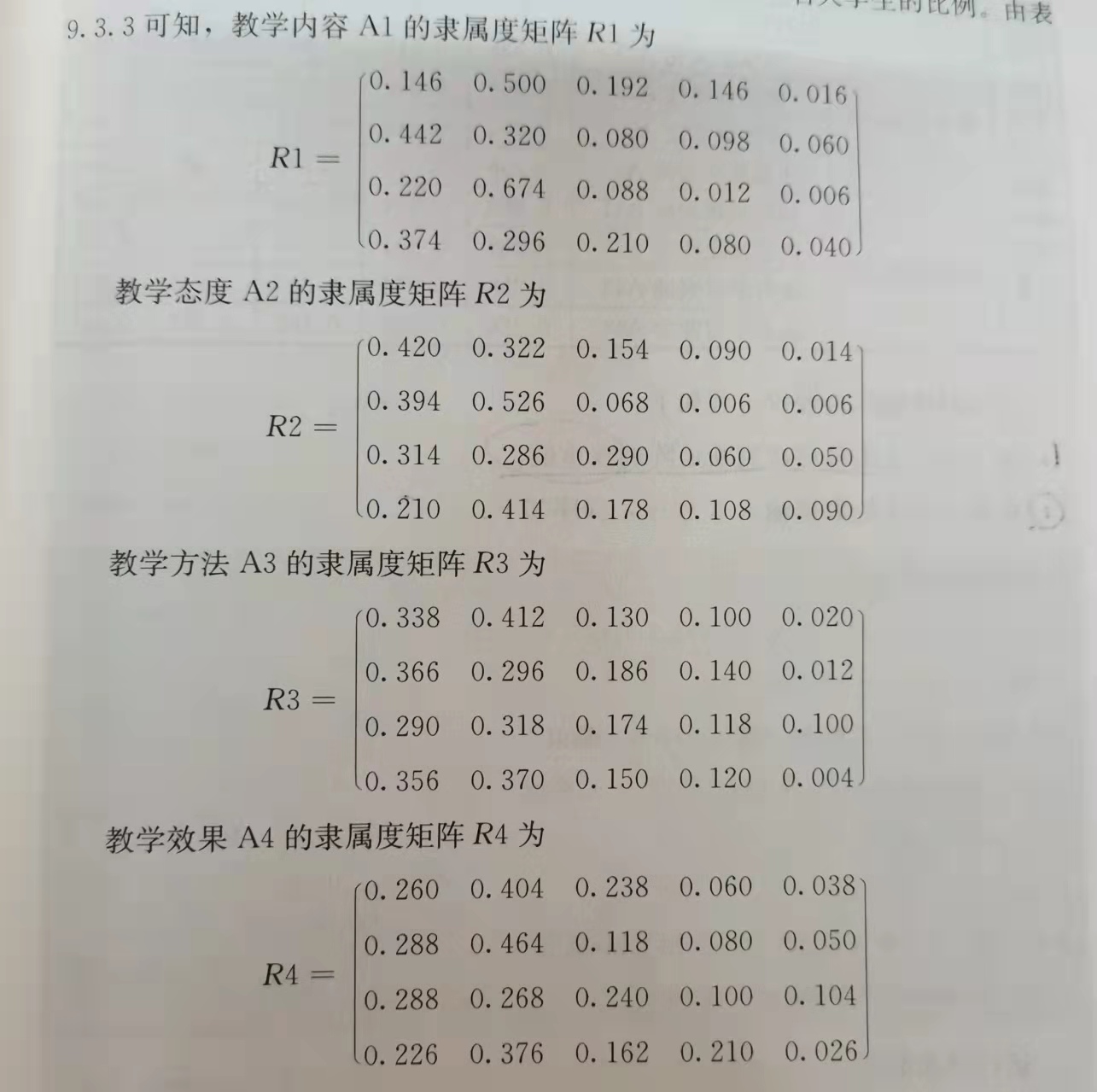
代码：

#运用模糊隶属度矩阵R/K与各层次判断矩阵权重W，求模糊评价

#下述r1,r2,r3,r4为隶属度矩阵，数字为500名大学生问卷在优良中可差五等级比例%

r1=c(0.146,0.500,0.192,0.146,0.016,0.442,0.320,0.080,0.098,0.060,0.220,0.674,0.088,0.012,0.006, 0.374,0.296,0.210,0.080,0.040)

r1=matrix(r1, ncol=5, byrow=T)

r2=c(0.420,0.322,0.154,0.090,0.014,0.394,0.526,0.068,0.006,0.006,0.314,0.286,0.290,0.060,0.050, 0.210,0.414,0.178,0.108,0.090)

r2=matrix(r2, ncol=5, byrow=T)

r3=c(0.338,0.412,0.130,0.100,0.020,0.366,0.296,0.186,0.140,0.012,0.290,0.318,0.174,0.118,0.100, 0.356,0.370,0.150,0.120,0.004)

r3=matrix(r3, ncol=5, byrow=T)

r4=c(0.260,0.404,0.238,0.060,0.038,0.288,0.464,0.118,0.080,0.050,0.288,0.268,0.240,0.100,0.104, 0.226,0.376,0.162,0.210,0.026)

r4=matrix(r4, ncol=5, byrow=T)

#教学质量单因素一级模糊评价k1,k2,k3,k4

k1=w21%*%r1

k2=w22%*%r2

k3=w23%*%r3

k4=w24%*%r4

#教学质量综合二级评价p

k=c(k1,k2,k3,k4)

k=matrix(k, ncol=5, byrow=T)

#k为一级模糊评价矩阵

#我们最终想得到的是二级模糊综合评估

#即用矩阵K和前面求得的判断矩阵的权重w，做矩阵相乘

p=w1%*%k

--------------------------------以上便是全部代码-----------------------------------------------------------

----------------------下面我给出最后二级模糊综合评估的结果，教大家如何分析结果-----------------------

分析：

27.83%为优，40.72%为良，16.68%为中，11.12%为可，3.65%为差。

大小比较：40.72%>27.83%>16.68%>11.12%>3.65%

所以综合评价结果为“良”。

 

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

【还不知道要怎么用改数据的看下面这个例子】

除去教学效果，即不需要r4了，也就不需要计算w24了。

修改后代码：

#专家判断矩阵目标层

a=c(1,5,3, 1/5,1,1/3, 1/3,3,1)

a=matrix(a, ncol=3, byrow=T)

ev=eigen(a)

#取出数组第一个值

lamda=ev$values[1]

cil=(lamda-3)/3

crl=cil/0.58

w1=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层1 教学内容

b1=c(1,3/5,3/7, 5/3,1,5/7, 7/3,7/5,1)

b1=matrix(b1, ncol=3, byrow=T)

ev=eigen(b1)

lamda=ev$values[1]

ci21=(lamda-3)/3

cr21=ci21/0.58

cr21

w21=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层2 教学态度

b2=c(1,7/5,7, 5/7,1,5, 1/7,1/5,1)

b2=matrix(b2, ncol=3, byrow=T)

ev=eigen(b2)

lamda=ev$values[1]

ci22=(lamda-3)/3

cr22=ci22/0.58

cr22

w22=ev$vectors[,1]/sum(ev$vectors[,1])

#准则层3 教学方法

b3=c(1,5/3,5, 3/5,1,3, 1/5,1/3,1)

b3=matrix(b3, ncol=3, byrow=T)

ev=eigen(b3)

lamda=ev$values[1]

ci23=(lamda-3)/3

cr23=ci23/0.58

cr23

w23=ev$vectors[,1]/sum(ev$vectors[,1])

#底下 r1,r2,r3为隶属度矩阵，数字为500名大学生问卷在优良中可差五等级比例%

r1=c(0.146,0.500,0.192,0.146,0.016,0.442,0.320,0.080,0.098,0.060,0.220,0.674,0.088,0.012,0.006, 0.374,0.296,0.210,0.080,0.040)

r1=matrix(r1, ncol=5, byrow=T)

r2=c(0.420,0.322,0.154,0.090,0.014,0.394,0.526,0.068,0.006,0.006,0.314,0.286,0.290,0.060,0.050, 0.210,0.414,0.178,0.108,0.090)

r2=matrix(r2, ncol=5, byrow=T)

r3=c(0.338,0.412,0.130,0.100,0.020,0.366,0.296,0.186,0.140,0.012,0.290,0.318,0.174,0.118,0.100, 0.356,0.370,0.150,0.120,0.004)

r3=matrix(r3, ncol=5, byrow=T)

#教学质量单因素一级模糊评价k1,k2,k3

k1=w21%*%r1

k2=w22%*%r2

k3=w23%*%r3

#教学质量综合二级评价p

k=c(k1,k2,k3)

k=matrix(k, ncol=5, byrow=T)

p=w1%*%k

最后

以上就是碧蓝酒窝为你收集整理的R语言-模糊逻辑控制4.3实例-对教学质量的评价：代码： -----------------以下数据仍是需要自己调查计算出来的-----------------代码：分析：的全部内容，希望文章能够帮你解决R语言-模糊逻辑控制4.3实例-对教学质量的评价：代码： -----------------以下数据仍是需要自己调查计算出来的-----------------代码：分析：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。