台湾国立大学郭彦甫Matlab教程笔记（4）matrix

replacing entries取代某个位置某个数值

目前A矩阵是这个样子

现在需要练习到后面这个矩阵

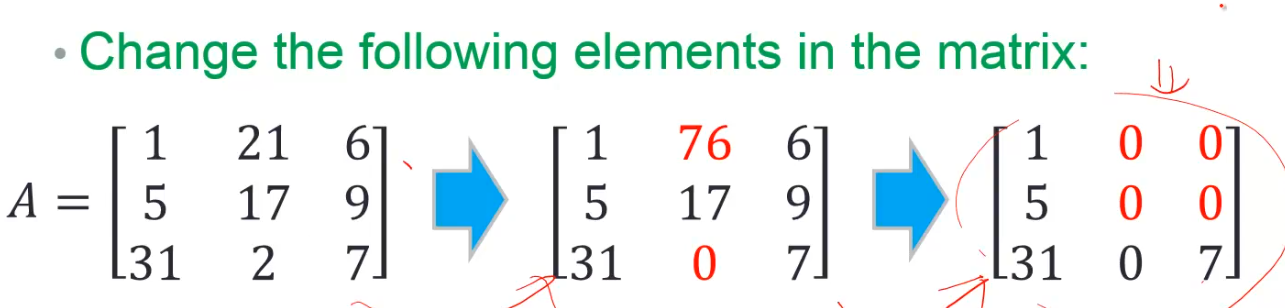
练习的步骤：

现在的问题是：如何把右上角的4个位置赋值为同一个数。

运用上一笔记中的用法,链接https://blog.csdn.net/shizheng_Li/article/details/99642215
截图：

我们要实现 四个坐标同时为0，可以这样来做
A([1 2],[2 3])=0
表示的是，一行两列，一行三列，两行两列，两行三列位置的元素赋值为0，达到效果。

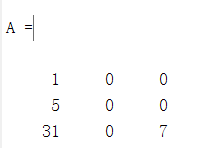
综上，我们的练习完成了。

colon operator 冒号运算符

用来做等差数列的宣告，
want to create a long array:A=[1 2 3 4 … 100]
1.create vectors or arrays,and specify for iterations重复
2.syntax句法，语法：
j:i:k:
j is the first number ,k is the last number ,i is the step length
if there is no i, such as j:k,it represents that the step length is 1


我的练习
1.b=1:5 表示的是1，2，3，4，5这样一个row vector
2 b=1:2:5，表示的是1，3，5这样一个row vector，因为步长是2
3.我们运行一下第三个题目
得到的是一个matrix，

你看，自己在做的时候，可能会出现手误，这样造成数组的维度不一致，就不能构造出一个矩阵，因为列数不匹配嘛。
4.colon 可以和字符串一起用哦，比如第四题

步长是2， 这样从a到z就是把间隔为1（步长是2，做差等于2，就是中间隔了一个字母）的字母全部输出来。

做完这个例题，我们再回到矩阵A

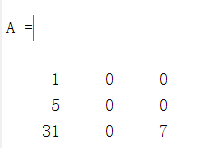
我们现在的需求是把A矩阵的第三行删除掉，怎么做？
只需要这样：A(3,:)=[]，这句话的意思是 选择第三行A(3,:)，后面的冒号colon表示的是所有的列
然后用一个空的中括号，就是表示删除

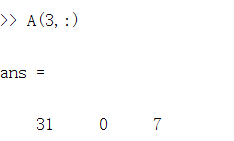
array concatenation 矩阵连接

1.array can be formed through concatenation as long as the rectangle shape is preserved

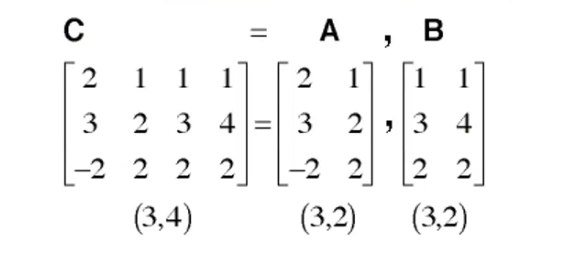
下面先给出两个小矩阵A和B

现在需要得到A和B的增广矩阵，F，这就是一个 concatenation
可以通过F=[A B]，把他们放在同一个中刮号，中间用space 隔开

老师一个问题，如果中间不用space隔开，而是用semicolon隔开会怎样？

中间用了 semicolon分号，结果是两个矩阵A和B的连接方向变掉了，改为纵向连接

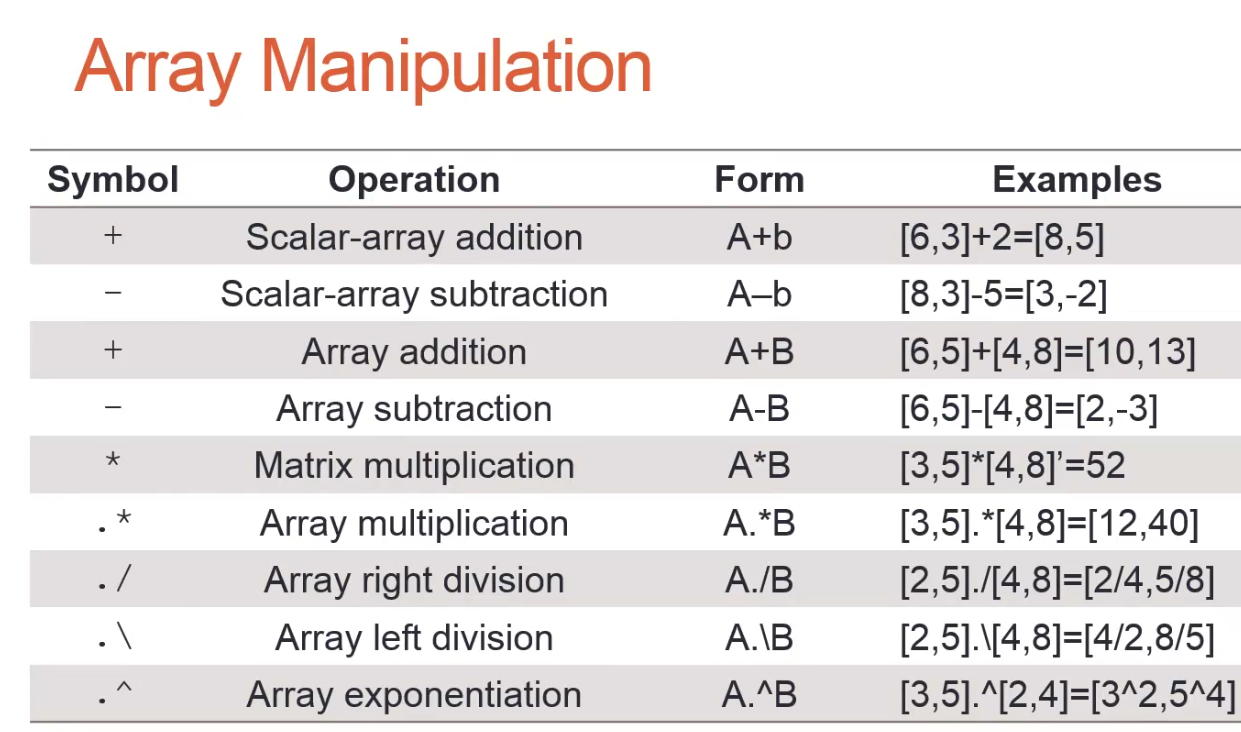
array manipulation 矩阵跟向量的四维运算

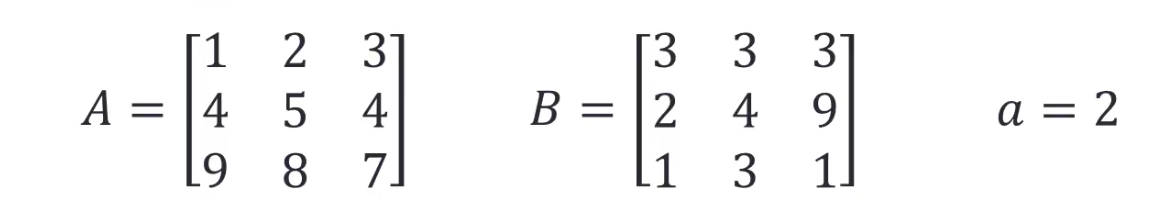
1.operators on array:+ - * / ^ . ’

矩阵的乘法A*B：第一个entry是什么？第一个row乘以另一个矩阵的第一个column，第二个呢？等于第一个row乘以另一个矩阵的第二个column

矩阵的点乘 A.*B 对应的entry相乘放在同一个地方

有同学会问，有没有点加？没有点加，因为加号的定义就是点加，其实，对应位置的元素相加

同样矩阵的除法，类似于A* inv（B）
而矩阵的点除，是对应位置相除
我们在Matlab中看一下运行效果

1.矩阵的加法

2。矩阵的乘法：A的每一个ROW乘以B的一个column，汇总相加，所以看起来数值比较大

3.矩阵的点乘
A的某一个位置 乘以B的对应位置

4.矩阵的除法，这里先不讲

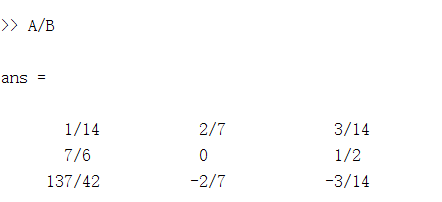
5.矩阵的点除：对应位置的entry相除

点除在这里：加一句 format rat 使之显示格式为分数形式，这个对比来看更直观

6.下面来看矩阵和一个常数a之间的运算
6.1.矩阵与常数相加，matrix对应位置加常数a

6.2.矩阵和常数相除，因为a是一个常数，所以A/a和A./a的结果是一样的

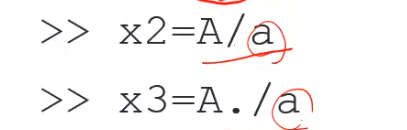
运算结果：

6.3.矩阵的次方，A^2=AA,矩阵相乘

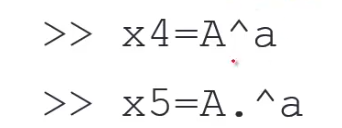
矩阵的次方运算结果：就是AA

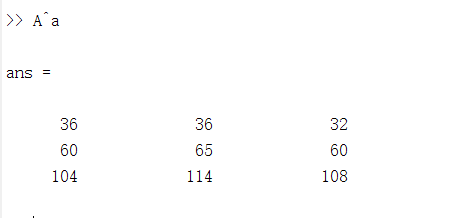
A.^2表示的是矩阵里面的每个entry都取两次方，
A矩阵长这样

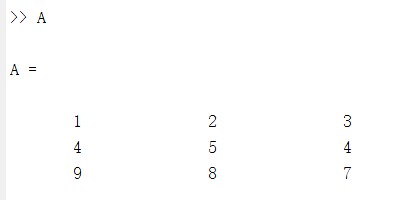
A加点之后平方的结果：每个位置都平方

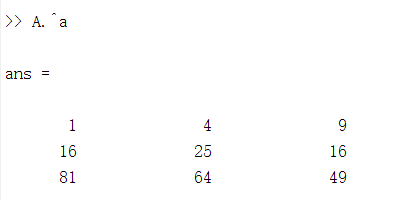
7.矩阵的转置 ‘
矩阵的行和列交换

some special matrix

linspace() :linearly spaced vectors
2.
eye(n):n*n identity matrix ，主对角线矩阵
3.
zero(n1,n2):zero matrix
4.
ones(n1,n2):matrix with every entry as 1
5.
diag():diagonal matrix 对角矩阵，只有对角线有值

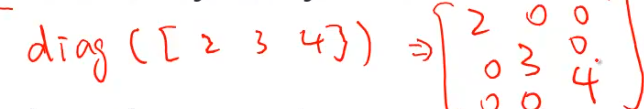
给出一个A矩阵

一，数值计算类
1.执行max（A），给出的是每一个column最大数是多少。因为矩阵matrix是一列一列排布的

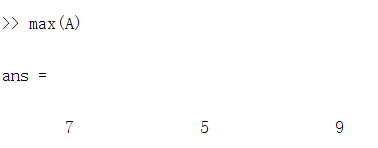
2.想要知道一个矩阵中的某一个位置的最大数是多少，这样：max（max(A)）

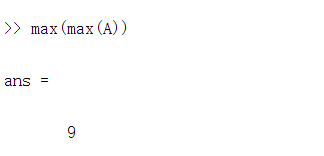
得到矩阵A中最大的数字是9
3.min(A)得到的是每一列的最小值

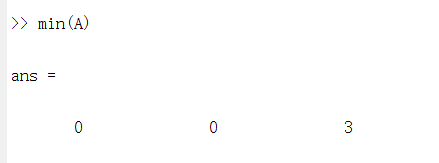
4.得到一个矩阵中最小的一个数字min(min(A))

5,每一个column的加总:sum(A)
一个矩阵所有元素的和sum(sum(A))
6.每一个column的平均值：mean(A)
一个matrix的所有元素的平均值 mean(mean(A))

二，矩阵整体信息
1.每一个column排序：sort(A)
每一列都按照从小到大的顺序排序

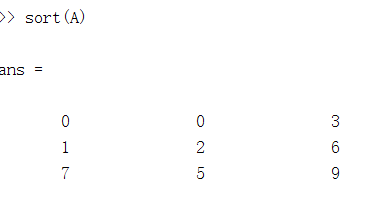
2.sortrows(A)
每一个row是绑在一起的，按照第一列大小重排每一行

3.size(A)看 矩阵每一个 dimension多大，得到的是3行，三列

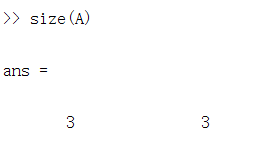
4.length(A),是vector的长度，一维的

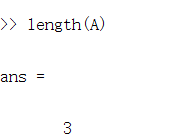
5.find(A==5)找矩阵中等于5的是哪个位置

最后

以上就是细心星月为你收集整理的台湾国立大学郭彦甫Matlab教程笔记（4）matrix的全部内容，希望文章能够帮你解决台湾国立大学郭彦甫Matlab教程笔记（4）matrix所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。