泛读HAN

之前的GNN专题里面有涉及到异质图的文章有三篇，分别是：
04metapath2vec
05transE
06GAT
这次要讲的是：Heterogeneous Graph Attention Network
文章发表在The 2019 World Wide Web Conference（CCF A类会议）
是一篇异质图经典的Baseline。

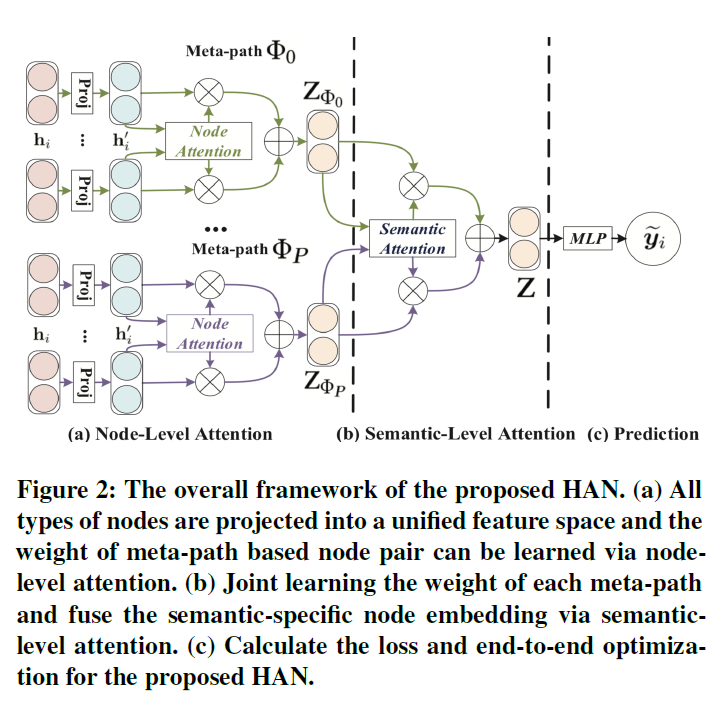
文章中表明，和简单图不一样（节点类型和边类型均只有1种，那么二者之和等于2）该文章研究的图的节点类型和边类型之和要大于2。
$$|\mathcal{A}|+|\mathcal{R}|>2$$
不同类型的节点，表示他们特征的特征空间是不一样的，甚至维度也都不一样，例如，作者、文章的维度不一样，因此要对不同类型的节点或边，先进行projection：
$$h_i^{\prime }=M_{{\Phi }_i}\cdot h_i$$
这样的好处是可以把不同特征空间的向量映射到相同空间上，不然不同维度的向量无法进行加减之类的运算。
这个模型每个metapath都会为节点计算一套特征表示，因此在某个metapath（不同metapath用不同的$\varphi$表示）下的节点间($h_i^{\prime },h_j^{\prime }$)注意力（node-level attention）可以表示为：
$$e_{ij}^{\Phi }=at{t}_{node}(h_i^{\prime },h_j^{\prime };\Phi )$$
然后要把上面的注意力用softmax进行归一化（原因之前有说过，每个节点邻居数量不一样，数量少的比数量多的权重算出来要大，因此归一化后才能进行比较）
$$\begin{array}{rl}{\alpha }_{ij}^{\Phi }& =softma{x}_j(e_{ij}^{\Phi })\\ & =\frac{\exp \left(\sigma (a_{\Phi }\cdot [h_i^{\prime }||h_j^{\prime }])\right)}{{\sum }_{k\in {\mathcal{N}}_i^{\Phi }}\exp \left(\sigma (a_{\Phi }\cdot [h_i^{\prime }||h_j^{\prime }])\right)}\end{array}$$
其中$\sigma$是激活函数，$h_i^{\prime }||h_j^{\prime }$表示concat，$a_{\Phi }$是metapath $\Phi$的节点注意力向量，带T表示转置。
然后节点$i$信息的汇聚表示为：
$$z_i^{\Phi }=\sigma \left(\sum _{j\in {\mathcal{N}}_i^{\Phi }}{\alpha }_{ij}^{\Phi }\cdot h_j^{\prime }\right)$$
文章还把node-level attention进行了扩展，变成multihead attention，就是将node-level attention重复K次，然后把得到的embedding进行拼接。
$$z_i^{\Phi }=|{|}_1^K\sigma \left(\sum _{j\in {\mathcal{N}}_i^{\Phi }}{\alpha }_{ij}^{\Phi }\cdot h_j^{\prime }\right)$$
以上是单个metapath $\Phi$的节点embedding的计算，针对多个metapath： { Φ 1 , Φ 2 , ⋯   , Φ P } {Phi_1,Phi_2,cdots,Phi_P} {Φ1​,Φ2​,⋯,ΦP​}，就会得到多个embedding： { Z Φ 1 , Z Φ 2 , ⋯   , Z Φ P } {Z_{Phi_1},Z_{Phi_2},cdots,Z_{Phi_P}} {ZΦ1​​,ZΦ2​​,⋯,ZΦP​​}。
对应的图如下所示，每个metapath就是一个圈圈，每个metapath的邻居都不一样：

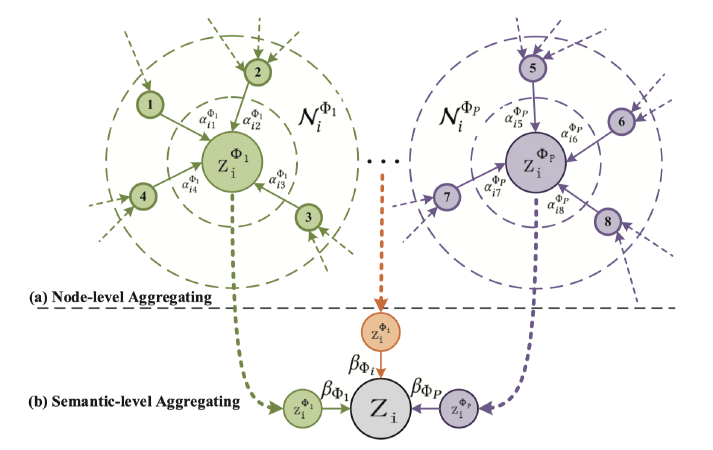
上面根据节点间的注意力在不同的metapath下算出来了$Z$，但是：
不同的metapath能不能有attention？在原文的4.2节就提出了：Semantic-level Attention，计算的就是每个metapath对应的embedding的重要程度，因此引入新的注意力权重：$\beta$，每个metapath都有权重，就可以表示为：$({\beta }_{{\Phi }_1},{\beta }_{{\Phi }_2},\cdots ,{\beta }_{{\Phi }_P})$，计算方法为：
$$({\beta }_{{\Phi }_1},{\beta }_{{\Phi }_2},\cdots ,{\beta }_{{\Phi }_P})=at{t}_{sem}(Z_{{\Phi }_1},Z_{{\Phi }_2},\cdots ,Z_{{\Phi }_P})$$
先算重要程度，在归一化，重要程度计算时先经过MLP（就是tanh那个部分）然后点乘Semantic level Attention的向量$q$的转置，得到一个实数，这个实数就是：
$$w_{{\Phi }_p}=\frac{1}{|\mathcal{V}|}\sum _{i\in \mathcal{V}}{q}^T\cdot \tanh (W\cdot z_i^{{\Phi }_p}+b)$$
这里的$|\mathcal{V}|$表示metapath ${\Phi }_p$下的所有节点集合。
接下来归一化：
$${\beta }_{{\Phi }_P}=\frac{\exp (w_{{\Phi }_p})}{{\sum }_{p=1}^P\exp (w_{{\Phi }_p})}$$
思考：为什么计算$w_{{\Phi }_p}$已经根据节点个数求了平均，还要进行归一化？
最后的节点的embedding表示为：
$$Z=\sum _{p=1}^P{\beta }_{{\Phi }_P}\cdot Z_{{\Phi }_P}$$.

DGL创建异质图

源代码看这里

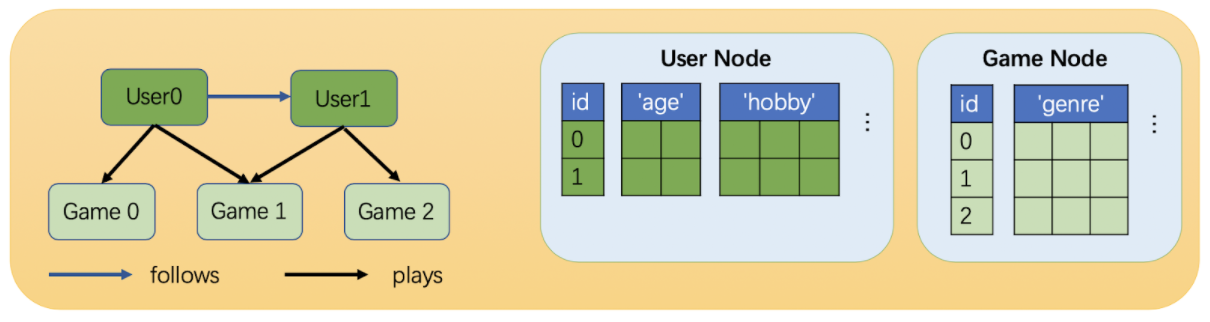
可以看到用户节点和游戏节点维度是不一样的。但是我们可以通过分别乘以矩阵将他们映射到相同维度上。

多类型节点和边的异质图

在DGL中，使用的三元组来表示异质图的关系：
（源节点类型，边类型，目的节点类型）
例如：

import dgl
import torch as th

# Create a heterograph with 3 node types and 3 edges types.
graph_data = {
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'interacts', 'gene'): (th.tensor([0, 1]), th.tensor([2, 3])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))
}
g = dgl.heterograph(graph_data)

得到结点类型：g.ntypes
[‘disease’, ‘drug’, ‘gene’]
边类型：g.etypes，这里interacts类型出现两次，因为interacts连接的节点类型都不一样，就好比药物和药物的影响与药物与基因的影响都是叫影响，但是二者的影响是不一样的。
[‘interacts’, ‘interacts’, ‘treats’]
三元组关系：g.canonical_etypes
[(‘drug’, ‘interacts’, ‘drug’),
(‘drug’, ‘interacts’, ‘gene’),
(‘drug’, ‘treats’, ‘disease’)]
图的信息：g
Graph(num_nodes={‘disease’: 3, ‘drug’: 3, ‘gene’: 4},
num_edges={(‘drug’, ‘interacts’, ‘drug’): 2, (‘drug’, ‘interacts’, ‘gene’): 2, (‘drug’, ‘treats’, ‘disease’): 1},
metagraph=[(‘drug’, ‘drug’, ‘interacts’), (‘drug’, ‘gene’, ‘interacts’), (‘drug’, ‘disease’, ‘treats’)])
这里要注意，虽然disease只有一个节点，但是其节点编号是2，因此这里按索引来算，它显示的是0.1.2,3个结点，或者说这里不是指节点数量，而是索引最大值+1。
边信息：g.metagraph().edges()
OutMultiEdgeDataView([(‘drug’, ‘drug’), (‘drug’, ‘gene’), (‘drug’, ‘disease’)])
打印disease类型节点：g.nodes(‘disease’)，这里由于节点有多个类型，不能直接使用g.nodes()，会报错。
tensor([0, 1, 2])
其实0和1根本不是disease
为节点设置特征：g.edges[‘edge_type’].data[‘feat_name’].

# Set/get feature 'hv' for nodes of type 'drug'
g.nodes['drug'].data['hv'] = th.ones(3, 1)
g.nodes['drug'].data['hv']

结果：
tensor([[1.],
[1.],
[1.]])

单类型节点和多类型边的异质图

下面创建一个只有一个节点类型的异质图：

g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'is similar', 'drug'): (th.tensor([0, 1]), th.tensor([2, 3]))
})

由于节点类型只有一种，这个时候可以用：
g.nodes()#打印节点信息
结果：
tensor([0, 1, 2, 3])
特征初始化：

# To set/get feature with a single type, no need to use the new syntax
g.ndata['hv'] = th.ones(4, 1)

异质图的条件子图

g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'interacts', 'gene'): (th.tensor([0, 1]), th.tensor([2, 3])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))
})
g.nodes['drug'].data['hv'] = th.ones(3, 1)
# Retain relations ('drug', 'interacts', 'drug') and ('drug', 'treats', 'disease')
# All nodes for 'drug' and 'disease' will be retained
#按两个条件提取子图
eg = dgl.edge_type_subgraph(g, [('drug', 'interacts', 'drug'),
                                ('drug', 'treats', 'disease')])

# The associated features will be copied as well
## 切割后的特征也会保留
eg.nodes['drug'].data['hv']

打印子图信息：eg
Graph(num_nodes={‘disease’: 3, ‘drug’: 3},
num_edges={(‘drug’, ‘interacts’, ‘drug’): 2, (‘drug’, ‘treats’, ‘disease’): 1},
metagraph=[(‘drug’, ‘drug’, ‘interacts’), (‘drug’, ‘disease’, ‘treats’)])

异质图转同质图

先创建一个异质图：

g = dgl.heterograph({
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))})
g.nodes['drug'].data['hv'] = th.zeros(3, 1)
g.nodes['disease'].data['hv'] = th.ones(3, 1)
g.edges['interacts'].data['he'] = th.zeros(2, 1)
g.edges['treats'].data['he'] = th.zeros(1, 2)

转同质图：

hg = dgl.to_homogeneous(g)

转化后特征都没有了：

'hv' in hg.ndata

结果：false
要重新拷贝，拷贝的时候要注意，同质图中的边和节点特征都是同一维度，边的维度如果不一样，就会报错：

# Copy edge features
# For feature copy, it expects features to have
# the same size and dtype across node/edge types
hg = dgl.to_homogeneous(g, edata=['he'])
DGLError: Cannot concatenate column ‘he’ with shape Scheme(shape=(2,), dtype=torch.float32) and shape Scheme(shape=(1,), dtype=torch.float32)

拷贝节点特征没问题：

# Copy node features
hg = dgl.to_homogeneous(g, ndata=['hv'])
hg.ndata['hv']

结果：
tensor([[1.],
[1.],
[1.],
[0.],
[0.],
[0.]])

在操作过程中，可按某个边类型切割异质图的子图，然后做转化为同质图后做操作。

最后

以上就是舒适棉花糖为你收集整理的第三周.02.HAN算法详解泛读HANDGL创建异质图的全部内容，希望文章能够帮你解决第三周.02.HAN算法详解泛读HANDGL创建异质图所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。