概述
Apollo 中横向控制的LQR控制算法
在Latcontroller..cc 中实现
根据车辆的二自由度动力学模型
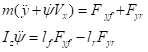(1)
根据魔术公式在小角度偏角的情况下有,轮胎的侧向力与轮胎的偏离角成正比. ,分别为前、后轮的侧偏刚度,
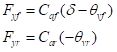(2)
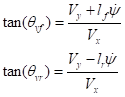(3)在小角度的情况下有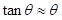
所以有
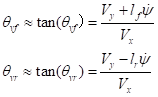(4)
因此上述车辆的动力学模型可以简化写成
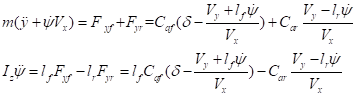(5)
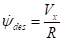(6)期望横摆角角速度
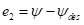(7) 横摆角角度偏差
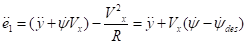(7)横向偏差变化率求导数
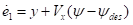(8)横向偏差变化率
车辆模型的连续状态空间方程
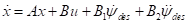(9)
状态变量X的选择分别为横向偏差、横向偏差变化率，横摆角角度偏差，横摆角角度偏差变化率。控制量u为前轮偏角。
选择合适的状态变量后得到A，B，B1，B2矩阵分别如下
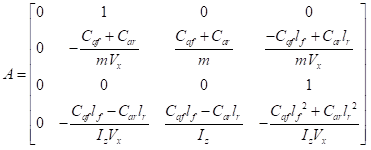
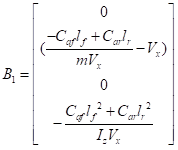
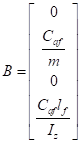
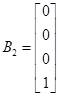
由于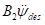
只对横摆角角度偏差变化率的导数产生影响，在横向控制中主要是控制横向偏差、横向偏差变化率，横摆角角度偏差，横摆角角度偏差变化率，因而忽略了公式中
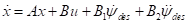的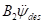
项。车辆系统的状态空间方程表示为
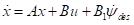(10)
Init（）函数中将A,B, 与Vx无关的系数先行计算，与Vx相关的系数参数计算根据Vx不断更新。
上述连续的状态空间方程用于计算机控制需要对连续的状态空间方程进行离散化，其中At采用双线性变换得到
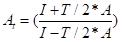, At来源见右边公式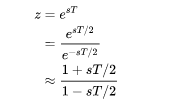
, 
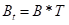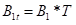，T为控制周期，本程序中为0.01s。
上述参数计算和离散化的过程在UpdateMatrix()函数和UpdateMatrixCompound()函数中
的离散化过程在Init（）函数中实现
matrix_b_ = Matrix::Zero(basic_state_size_, 1);
matrix_bd_ = Matrix::Zero(basic_state_size_, 1);
matrix_bdc_ = Matrix::Zero(matrix_size, 1);
matrix_b_(1, 0) = cf_ / mass_;
matrix_b_(3, 0) = lf_ * cf_ / iz_;
matrix_bd_ = matrix_b_ * ts_;
的离散化过程在UpdateMatrix()函数中实现
void LatController::UpdateMatrix() {
const double v =
std::max(VehicleStateProvider::instance()->linear_velocity(), 0.2);
matrix_a_(1, 1) = matrix_a_coeff_(1, 1) / v;
matrix_a_(1, 3) = matrix_a_coeff_(1, 3) / v;
matrix_a_(3, 1) = matrix_a_coeff_(3, 1) / v;
matrix_a_(3, 3) = matrix_a_coeff_(3, 3) / v;
Matrix matrix_i = Matrix::Identity(matrix_a_.cols(), matrix_a_.cols());
matrix_ad_ = (matrix_i + ts_ * 0.5 * matrix_a_) *
(matrix_i - ts_ * 0.5 * matrix_a_).inverse(); //双线性变换离散化A
}
通过上述介绍我们得到了车辆离散状态空间方程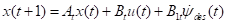
(11)中的At,Bt,则系统的最优前轮转角
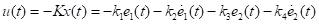(12)
定义如下目标函数
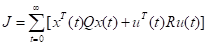(13)
其中Q为状态权重系数，R为控制量权重系数
当上述目标函数最小时就得到最优的状态反馈矩阵K
上述公式的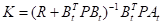
,(14)
同时矩阵P满足黎卡提方程：
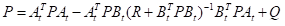(15)
求解状态反馈矩阵K的在
common::math::SolveLQRProblem(matrix_adc_, matrix_bdc_, matrix_q_,
matrix_r_, lqr_eps_, lqr_max_iteration_,
&matrix_k_); 函数中实现
函数输入为At,Bt,Q，R,最大迭代次数lqr_max_iteration_，最小精度lqr_eps_，函数输出为状态反馈矩阵matrix_k_。
当前最新的状态量是通过UpdateStateAnalyticalMatching()函数获得，由此我们可以通过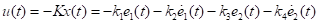
(12)
计算出当前的最优反馈控制量即最优前轮偏角。然而这还没玩完。
将公式(12)的控制量带入公式（10）得到系统状态反馈后的状态空间方程如下
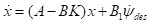(13)
车辆沿固定曲率的轨迹运行时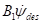
不为零。因此通过LQR调节
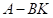的特征值使系统趋于稳定，但是系统的稳态偏差并不为0。
为此在原有最优控制量的基础上增加一个前馈环节，使系统趋于稳定的同时系统的横向稳态偏差为0。
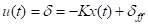(14)
公式中为前馈环节提供的前轮转角。
将公式(14)带入公式（10）得到
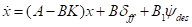(15)
设初始条件为0，对公式(15)进行拉普拉斯变换得到
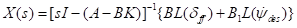(16)
假设汽车以固定纵向速度Vx沿某一固定曲率的弯道行驶，则通过纵向车速Vx和道路的半径R可以计算出期望汽车横摆角速度：
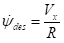(6)
公式(6)可知横摆角速度的拉普拉斯变换结果为
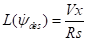(17)
假设为固定值，则其拉普拉斯变换结果为
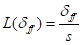(18)
根据终值定理，系统的稳态误差为
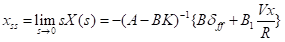(19)
将A，B,B1,K带入公式(19)得到
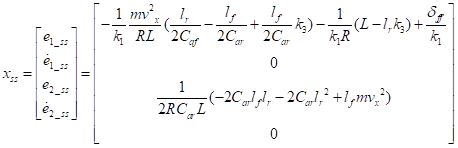(20)
观察公式(20)中的第一项和第三项。可知道对横摆角角度偏差无影响，选择合适的可将横向偏差稳态值趋向与0。
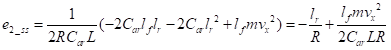(21)
要想横向偏差的稳态值趋于零，则
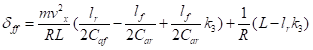(22)
因此
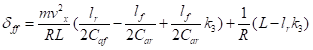(23)
令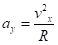
，不足转向梯度系数
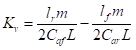(24)
公式(23)可以简化为
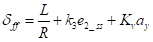(25)
Apollo程序中计算控制量的函数为ComputeControlCommand()函数
前馈环节计算的前轮转角对应如下程序
double LatController::ComputeFeedForward(double ref_curvature) const {
const double kv =
lr_ * mass_ / 2 / cf_ / wheelbase_ - lf_ * mass_ / 2 / cr_ / wheelbase_; //对应公式(24)
// then change it from rad to %
const double v = VehicleStateProvider::instance()->linear_velocity();
const double steer_angle_feedforwardterm =
(wheelbase_ * ref_curvature + kv * v * v * ref_curvature -
matrix_k_(0, 2) *
(lr_ * ref_curvature -
lf_ * mass_ * v * v * ref_curvature / 2 / cr_ / wheelbase_)) *
180 / M_PI * steer_transmission_ratio_ /
steer_single_direction_max_degree_ * 100; //对应公式(25),并将角度由弧度转变为角度，最后转变为百分比
return steer_angle_feedforwardterm;
}
最终的前轮转角的控制量为最优状态反馈控制量与前馈控制前轮转角之和。对应程序如下
const double steer_angle_feedback = -(matrix_k_ * matrix_state_)(0, 0) * 180 /
M_PI * steer_transmission_ratio_ /
steer_single_direction_max_degree_ * 100;
//计算状态反馈对应的控制量，将弧度转变为角度，最后转变为百分比。
// steer_transmission_ratio_表示方向盘转动角度与车轮转动角度的比值，在车辆信息中定义该参数，
// steer_single_direction_max_degree表示最大的方向盘转动的角度，单位为度
const double steer_angle_feedforward = ComputeFeedForward(debug->curvature());
//计算前馈控制对应的控制量
// Clamp the steer angle to -100.0 to 100.0
double steer_angle = common::math::Clamp(
steer_angle_feedback + steer_angle_feedforward, -100.0, 100.0); //将状态反馈的控制量与前馈控制控制量进行叠加，并进行限幅处理。
计算的出前轮转角经过上下限的限幅后进行输出
if (FLAGS_set_steer_limit) {
const double steer_limit =
std::atan(max_lat_acc_ * wheelbase_ /
(VehicleStateProvider::instance()->linear_velocity() *
VehicleStateProvider::instance()->linear_velocity())) *
steer_transmission_ratio_ * 180 / M_PI /
steer_single_direction_max_degree_ * 100; //计算前轮转角的上下限限幅值。
// Clamp the steer angle
double steer_angle_limited =
common::math::Clamp(steer_angle, -steer_limit, steer_limit); //对前轮转角进行上下限的限幅处理
steer_angle_limited = digital_filter_.Filter(steer_angle_limited); //对前轮转角进行低通滤波处理
cmd->set_steering_target(steer_angle_limited);
debug->set_steer_angle_limited(steer_angle_limited);
} else {
steer_angle = digital_filter_.Filter(steer_angle);//对前轮转角进行低通滤波处理
cmd->set_steering_target(steer_angle);
}
部分成员函数介绍
1、LoadControlConf 成员函数用于获取控制参数包括车身参数、LQR控制的精度、最大迭代次数等。
其中车辆的参数来自modulescommondata mkz_config.pb.txt文件
LQR的控制参数来自modulescontrolconf lincoln.pb.txt文件
2、InitializeFilters成员函数用于设置巴斯沃特低通低通滤波参数， 以及对 lateral_error、heading_error进行均值滤波。滤波器的参数来自modulescontrolconf lincoln.pb.txt文件
3、Init成员函数用于初始化 状态空间方程的A，B，K, Q，R 以及控制系统的相关参数。
LoadLatGainScheduler函数的作用？
LoadLatGainScheduler函数用于获取 lateral_error、heading_error 增益的策略。
4、ComputeControlCommand 函数最重要，计算控制量
通过LQR求解黎卡提方程得到控制量
SolveLQRProblem(matrix_adc_, matrix_bdc_, matrix_q_updated_,
matrix_r_, lqr_eps_, lqr_max_iteration_,
&matrix_k_);
//在高速运行时，控制量权重矩阵matrix_q_的系数根据速度变化进行调整
// Add gain sheduler for higher speed steering
if (FLAGS_enable_gain_scheduler) {
matrix_q_updated_(0, 0) =
matrix_q_(0, 0) *
lat_err_interpolation_->Interpolate(
VehicleStateProvider::instance()->linear_velocity());
matrix_q_updated_(2, 2) =
matrix_q_(2, 2) *
heading_err_interpolation_->Interpolate(
VehicleStateProvider::instance()->linear_velocity());
common::math::SolveLQRProblem(matrix_adc_, matrix_bdc_, matrix_q_updated_,
matrix_r_, lqr_eps_, lqr_max_iteration_,
&matrix_k_);
} else {
common::math::SolveLQRProblem(matrix_adc_, matrix_bdc_, matrix_q_,
matrix_r_, lqr_eps_, lqr_max_iteration_,
&matrix_k_);
}
5、UpdateMatrix()函数
用于更新matrix_a_(离散之前的A矩阵) 和matrix_ad_（离散之后的A矩阵）
matrix_a_ 由中系数分为两类，一类与速度无关，另外一类与速度相关放在matrix_a_coeff_
从何得到线性时变状态空间方程。
matrix_adc_ 由matrix_ad_ 和 过去的变量对应的矩阵组合而成
matrix_bdc_. 由matrix_bd_ 和过去变量对应的矩组合而成。
6、GetLateralError()函数
获取横向偏差，具体计算过程为根据车辆当前的位置查找参考轨迹最近点，形成直线L。
计算出车辆位置与最近点的距离std::sqrt(dx * dx + dy * dy)，同时计算出该条线与x轴正方向之间的角度point_angle，将该角度减去参考轨迹的方向角得到直线L与参考轨迹速度方向之间的夹角point2path_angle。
横向偏差为std::sin(point2path_angle) * std::sqrt(dx * dx + dy * dy);
7、UpdateStateAnalyticalMatching()函数获取状态偏差，ComputeLateralErrors()函数主要通过根据当前车辆的位置计算出在参考轨迹上上离车辆当前位置最近点作为参考点，通过参考点与实际车辆位置就可以获得各种状态偏差（横向偏差、横向偏差变化率、航向角偏差、航向角偏差变化率）。
————————————————
版权声明：本文为CSDN博主「jm-csu」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weijimin1/article/details/85794084
最后
以上就是快乐微笑为你收集整理的Apollo 2.0 车辆控制算法LQR解析的全部内容，希望文章能够帮你解决Apollo 2.0 车辆控制算法LQR解析所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复