先上参考链接
【运动控制】Apollo6.0的mpc_controller解析
Apollo MPC OSQP Solver
详细的车辆横向动力学模型推导参考我另一篇博客
Apollo control模块横向控制原理及核心代码逐行解析
因为和上述链接里LQR控制的代码及框架类似，因此在此仅代码不赘述，主要介绍原理
MPC横纵向控制原理
一.mpc_controller框架
代码参见apollo/modules/control/controller/mpc_controller.cc
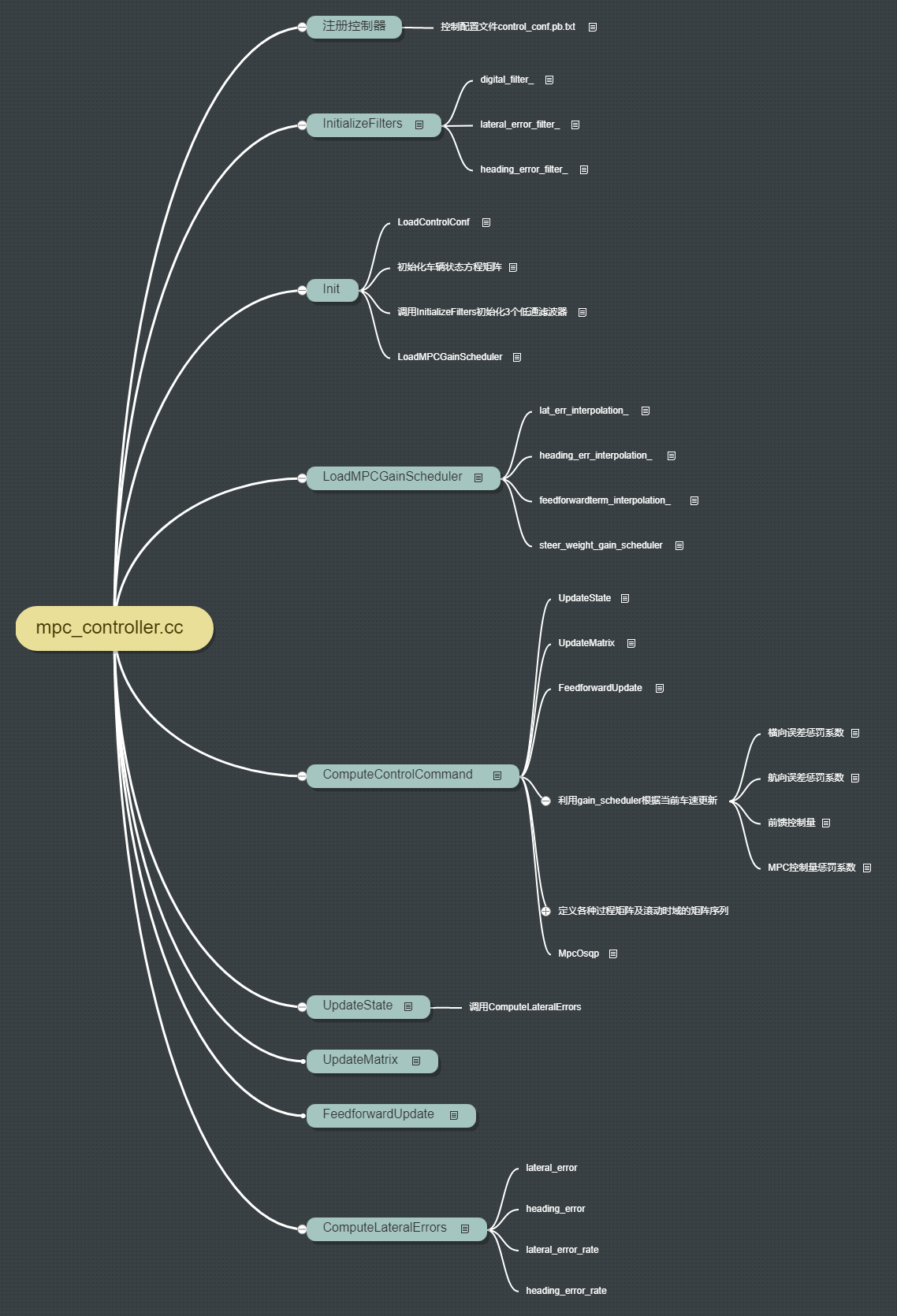
1.1 注册控制器
modulescontrolconfcontrol_conf.pb.txt里active_controllers: MPC_CONTROLLER
active_controllers: MPC_CONTROLLER
在这里激活不同的控制器。
LQR+PID 激活 LON_CONTROLLER + LAT_CONTROLLER
MPC控制只激活 MPC_CONTROLLER，横纵向耦合控制
1.2 InitializeFilters
初始化3个lpf低通滤波器
digital_filter_：二阶数字滤波器，用于对方向盘角度控制指令滤波
lateral_error_filter_：均值低通滤波器，对横向误差CTE进行滤波，滤波窗口大小mean_filter_window_size在control_conf.pb.txt种被定义为10个周期
heading_error_filter_：均值低通滤波器，对航向误差进行滤波，滤波窗口大小mean_filter_window_size同lateral_error_filter_
1.3 Init
1.3.1 LoadControlConf
LoadControlConf：加载控制配置文件中的参数到MPCLatController类的数据成员中
1.3.2 初始化车辆状态方程矩阵
车辆横向状态方程
X'=AX+Bu+B1*(φdes)'
初始化
A矩阵中常项，含速度项的后续继续处理；
B矩阵全常项，并 x ts进行离散化；
B1初始化为4x1的0矩阵；
X状态矩阵初始化为4x1的0矩阵；
MPC中的Q矩阵初始化4x4的矩阵，从配置文件读取；
MPC中的R矩阵初始化为1x1的单位矩阵，从配置文件读取；
1.3.3 调用InitializeFilters初始化3个低通滤波器
1.3.4 LoadMPCGainScheduler
从控制配置加载增益调度表
总共有4个增益调度表
lat_err_interpolation_：加载控制配置文件中的横向误差随车速的增益表到MPCController类数据成员，车速越大，Q矩阵中横向误差的权重系数就越小
heading_err_interpolation_：加载控制配置文件中的航向误差随车速的增益表到MPCController类数据成员，车速越大，Q矩阵中航向误差的权重系数就越小，低速偏重于横向误差，高速偏重于航向误差。
feedforwardterm_interpolation_：前馈项的增益表
steer_weight_gain_scheduler：控制量的增益表，R矩阵中控制量的惩罚系数 x 这个根据车速插值出来的ratio，车速越高，控制量的惩罚系数越大，ratio越大
1.4 ComputeControlCommand
UpdateState
函数作用：
1.计算横向控制所需的各个误差项，量放入debug指针；
2.更新车辆的状态矩阵matrix_state_，直接从上一步debug指针中取出横向/航项误差/误差率
UpdateMatrix
主要是更新车辆状态方程里的矩阵A,B1中与速度相关的项
matrix_a_
matrix_c_
FeedforwardUpdate
steer_angle_feedforwardterm_
主要是更新车辆状态方程里的前馈项里包含速度相关项
利用gain_scheduler根据当前车速更新
横向误差惩罚系数，航向误差惩罚系数，前馈控制量，MPC控制量惩罚系数
定义各种过程矩阵及滚动时域的矩阵序列
调用MpcOsqp优化求解器
输入各种参数及约束，调用modulescommonmathmpc_osqp.cc
调用MpcOsqp类的成员函数solve求解，求解的结果放入control控制序列里，取出第一个时刻的控制量下发。
这个控制量先进行转速限幅，滤波，再百分比限幅，最后下发。
1.5 UpdateState
函数作用：
1.调用ComputeLateralErrors计算横向控制所需的各个误差项，量放入debug指针；
2.更新车辆的状态矩阵matrix_state_，直接从上一步debug指针中取出横向/航项误差/误差率
1.6 UpdateMatrix
主要是更新车辆状态方程里的矩阵A,B1中与速度相关的项
matrix_a_
matrix_c_
1.7 FeedforwardUpdate
steer_angle_feedforwardterm_
主要是更新车辆状态方程里的前馈项里包含速度相关项
1.8 ComputeLateralErrors
计算横向误差相关量放入debug指针
二. mpc_osqp求解器
OSQP二次规划优化求解器,求解MPC问题，代码位于apollo/modules/common/math/mpc_osqp.cc里，定义了MpcOsqp类，主要实现了OSQP优化求解MPC问题的功能。
2.1 框架
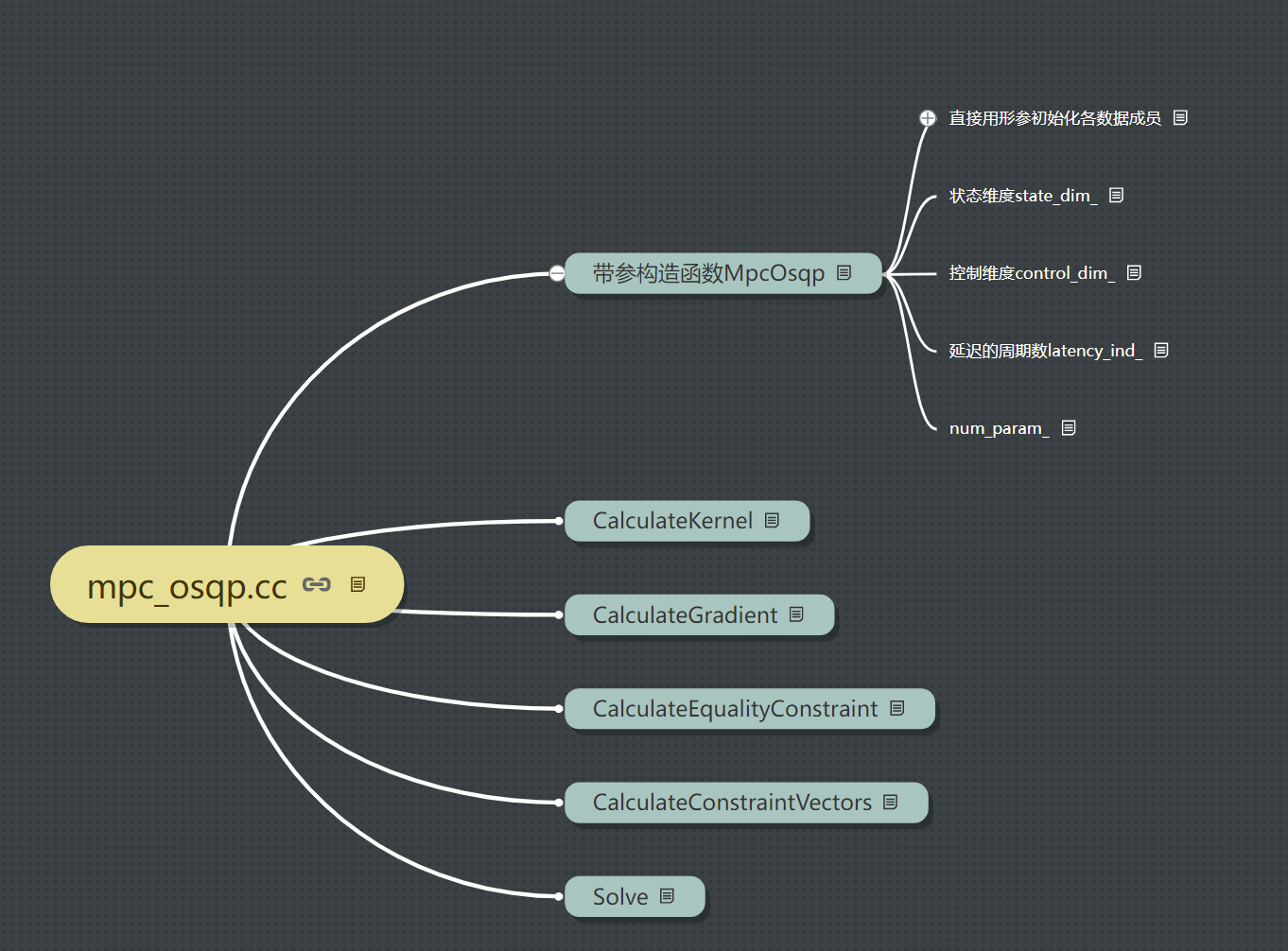
2.2 带参构造函数MpcOsqp
输入矩阵Ad,Bd,Q,R,初始状态阵X0,控制量上下边界，状态量上下边界，参考状态(0矩阵)，最大迭代次数mpc_max_iteration_，预测时域周期数horizon_，求解精度mpc_eps_，用输入参数去初始化类对象的数据成员
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30MpcOsqp::MpcOsqp(const Eigen::MatrixXd &matrix_a, const Eigen::MatrixXd &matrix_b, const Eigen::MatrixXd &matrix_q, const Eigen::MatrixXd &matrix_r, const Eigen::MatrixXd &matrix_initial_x, const Eigen::MatrixXd &matrix_u_lower, const Eigen::MatrixXd &matrix_u_upper, const Eigen::MatrixXd &matrix_x_lower, const Eigen::MatrixXd &matrix_x_upper, const Eigen::MatrixXd &matrix_x_ref, const int max_iter, const int horizon, const double eps_abs) : matrix_a_(matrix_a), matrix_b_(matrix_b), matrix_q_(matrix_q), matrix_r_(matrix_r), matrix_initial_x_(matrix_initial_x), matrix_u_lower_(matrix_u_lower), matrix_u_upper_(matrix_u_upper), matrix_x_lower_(matrix_x_lower), matrix_x_upper_(matrix_x_upper), matrix_x_ref_(matrix_x_ref), max_iteration_(max_iter), horizon_(horizon), eps_abs_(eps_abs) { state_dim_ = matrix_b.rows(); control_dim_ = matrix_b.cols(); ADEBUG << "state_dim" << state_dim_; ADEBUG << "control_dim_" << control_dim_; num_param_ = state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; }
state_dim_是状态矩阵的维度，等于矩阵Bd的行数
control_dim_是控制矩阵的维度，等于矩阵Bd的列数
num_param_是OSQP求解器待求解的变量X包含的参数个数
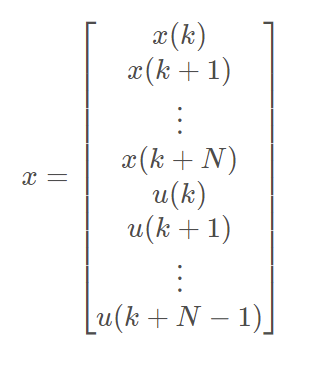
2.3 CalculateKernel
计算二次规划标准形式中的矩阵P
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40void MpcOsqp::CalculateKernel(std::vector<c_float> *P_data, std::vector<c_int> *P_indices, std::vector<c_int> *P_indptr) { // col1:(row,val),...; col2:(row,val),....; ... std::vector<std::vector<std::pair<c_int, c_float>>> columns; columns.resize(num_param_); size_t value_index = 0; // state and terminal state for (size_t i = 0; i <= horizon_; ++i) { for (size_t j = 0; j < state_dim_; ++j) { // (row, val) columns[i * state_dim_ + j].emplace_back(i * state_dim_ + j, matrix_q_(j, j)); ++value_index; } } // control const size_t state_total_dim = state_dim_ * (horizon_ + 1); for (size_t i = 0; i < horizon_; ++i) { for (size_t j = 0; j < control_dim_; ++j) { // (row, val) columns[i * control_dim_ + j + state_total_dim].emplace_back( state_total_dim + i * control_dim_ + j, matrix_r_(j, j)); ++value_index; } } CHECK_EQ(value_index, num_param_); int ind_p = 0; for (size_t i = 0; i < num_param_; ++i) { // TODO(SHU) Check this P_indptr->emplace_back(ind_p); for (const auto &row_data_pair : columns[i]) { P_data->emplace_back(row_data_pair.second); // val P_indices->emplace_back(row_data_pair.first); // row ++ind_p; } } P_indptr->emplace_back(ind_p); }
这个函数没有完全看明白，不过前两个for循环很好理解，就是将Q，R矩阵塞到QP问题的海森矩阵P里
2.4 CalculateGradient
计算二次规划标准形式中的矩阵q
1
2
3
4
5
6
7
8
9
10
11
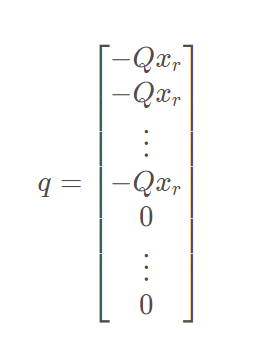
12// reference is always zero void MpcOsqp::CalculateGradient() { // populate the gradient vector gradient_ = Eigen::VectorXd::Zero( state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1); for (size_t i = 0; i < horizon_ + 1; i++) { gradient_.block(i * state_dim_, 0, state_dim_, 1) = -1.0 * matrix_q_ * matrix_x_ref_; } ADEBUG << "Gradient_mat"; ADEBUG << gradient_; }
不过这里呢，因为Apollo输入的参考状态矩阵matrix_x_ref始终是0其实这个q也始终是0矩阵吧
2.5 CalculateEqualityConstraint
计算二次规划约束中的矩阵Ac
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72void MpcOsqp::CalculateEqualityConstraint(std::vector<c_float> *A_data, std::vector<c_int> *A_indices, std::vector<c_int> *A_indptr) { static constexpr double kEpsilon = 1e-6; // block matrix Eigen::MatrixXd matrix_constraint = Eigen::MatrixXd::Zero( state_dim_ * (horizon_ + 1) + state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, state_dim_ * (horizon_ + 1) + control_dim_ * horizon_); Eigen::MatrixXd state_identity_mat = Eigen::MatrixXd::Identity( state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1)); ADEBUG << "state_identity_mat" << state_identity_mat; matrix_constraint.block(0, 0, state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1)) = -1 * state_identity_mat; ADEBUG << "matrix_constraint"; ADEBUG << matrix_constraint; Eigen::MatrixXd control_identity_mat = Eigen::MatrixXd::Identity(control_dim_, control_dim_); for (size_t i = 0; i < horizon_; i++) { matrix_constraint.block((i + 1) * state_dim_, i * state_dim_, state_dim_, state_dim_) = matrix_a_; } ADEBUG << "matrix_constraint with A"; ADEBUG << matrix_constraint; for (size_t i = 0; i < horizon_; i++) { matrix_constraint.block((i + 1) * state_dim_, i * control_dim_ + (horizon_ + 1) * state_dim_, state_dim_, control_dim_) = matrix_b_; } ADEBUG << "matrix_constraint with B"; ADEBUG << matrix_constraint; Eigen::MatrixXd all_identity_mat = Eigen::MatrixXd::Identity(num_param_, num_param_); matrix_constraint.block(state_dim_ * (horizon_ + 1), 0, num_param_, num_param_) = all_identity_mat; ADEBUG << "matrix_constraint with I"; ADEBUG << matrix_constraint; std::vector<std::vector<std::pair<c_int, c_float>>> columns; columns.resize(num_param_ + 1); int value_index = 0; // state and terminal state for (size_t i = 0; i < num_param_; ++i) { // col for (size_t j = 0; j < num_param_ + state_dim_ * (horizon_ + 1); ++j) // row if (std::fabs(matrix_constraint(j, i)) > kEpsilon) { // (row, val) columns[i].emplace_back(j, matrix_constraint(j, i)); ++value_index; } } ADEBUG << "value_index"; ADEBUG << value_index; int ind_A = 0; for (size_t i = 0; i < num_param_; ++i) { A_indptr->emplace_back(ind_A); for (const auto &row_data_pair : columns[i]) { A_data->emplace_back(row_data_pair.second); // value A_indices->emplace_back(row_data_pair.first); // row ++ind_A; } } A_indptr->emplace_back(ind_A); }
按照分块矩阵往Ac里塞A,B,I
Eigen库Eigen::MatrixXd定义矩阵分块操作函数.block()的用法
2.7 CalculateConstraintVectors
计算二次规划约束中的上边界，下边界矩阵l,u
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
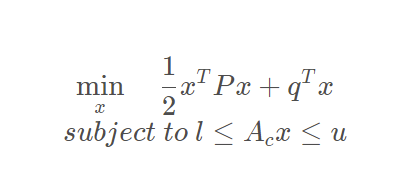
38void MpcOsqp::CalculateConstraintVectors() { // evaluate the lower and the upper inequality vectors Eigen::VectorXd lowerInequality = Eigen::MatrixXd::Zero( state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1); Eigen::VectorXd upperInequality = Eigen::MatrixXd::Zero( state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1); for (size_t i = 0; i < horizon_; i++) { lowerInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0, control_dim_, 1) = matrix_u_lower_; upperInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0, control_dim_, 1) = matrix_u_upper_; } ADEBUG << " matrix_u_lower_"; for (size_t i = 0; i < horizon_ + 1; i++) { lowerInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_lower_; upperInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_upper_; } ADEBUG << " matrix_x_lower_"; // evaluate the lower and the upper equality vectors Eigen::VectorXd lowerEquality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1), 1); Eigen::VectorXd upperEquality; lowerEquality.block(0, 0, state_dim_, 1) = -1 * matrix_initial_x_; upperEquality = lowerEquality; lowerEquality = lowerEquality; ADEBUG << " matrix_initial_x_"; // merge inequality and equality vectors lowerBound_ = Eigen::MatrixXd::Zero( 2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1); lowerBound_ << lowerEquality, lowerInequality; ADEBUG << " lowerBound_ "; upperBound_ = Eigen::MatrixXd::Zero( 2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1); upperBound_ << upperEquality, upperInequality; ADEBUG << " upperBound_"; }
2.8 Solve
根据输入的矩阵求解二次规划，求解结果取出控制序列放入cmd中，然后cmd中第一个控制量就可以用于控制了。
1bool MpcOsqp::Solve(std::vector<double> *control_cmd)
最后
以上就是迷你果汁最近收集整理的关于Apollo MPC横纵向耦合控制学习笔记MPC横纵向控制原理一.mpc_controller框架二. mpc_osqp求解器的全部内容，更多相关Apollo内容请搜索靠谱客的其他文章。
发表评论 取消回复