卷积神经网络(吴恩达深度学习p108-p150)
卷积网络
- 补充:超参数
- 机器学习模型中一般有两类参数:一类需要从数据中学习和估计得到,称为模型参数(Parameter)—即模型本身的参数。比如,线性回归直线的加权系数(斜率)及其偏差项(截距)都是模型参数。还有一类则是机器学习算法中的调优参数(tuning parameters),需要人为设定,称为超参数(Hyperparameter)。比如,正则化系数λ,决策树模型中树的深度。
- 参数和超参数的区别:模型参数是模型内部的配置变量,需要用数据估计模型参数的值;模型超参数是模型外部的配置,需要手动设置超参数的值。机器学习中一直说的“调参”,实际上不是调“参数”,而是调“超参数”。
- 哪些属于超参数?
梯度下降法中的学习速率α,迭代次数epoch,批量大小batch-size,k近邻法中的k(最相近的点的个数),决策树模型中树的深度,等等。 - 超参数的优化:
有四种主要的策略可用于搜索最佳配置:- 照看(babysitting,又叫试错)
- 网格搜索
- 随机搜索
- 贝叶斯优化
- 边缘检测示例:
- 注意所采用filter的样式,如垂直边缘检测一般采用的数字组合 [ 1 0 − 1 1 0 − 1 1 0 − 1 ] begin{bmatrix} 1& 0& -1 \1& 0& -1 \1& 0& -1 end{bmatrix} ⎣ ⎡111000−1−1−1⎦ ⎤; Sobel过滤器 [ 1 0 − 1 2 0 − 2 1 0 − 1 ] begin{bmatrix} 1& 0& -1 \2& 0& -2 \1& 0& -1 end{bmatrix} ⎣ ⎡121000−1−2−1⎦ ⎤,它的优点在于增加了中间一行元素的权重,这使得结果的鲁棒性会更高一些; Scharr过滤器 [ 3 0 − 3 10 0 − 10 3 0 − 3 ] begin{bmatrix} 3& 0& -3 \10& 0& -10 \3& 0& -3 end{bmatrix} ⎣ ⎡3103000−3−10−3⎦ ⎤。
- 一种思想:9个数字当成参数,使用反向传播去让神经网络学习这9个数字。
- 卷积操作——padding:
- 如果我们有一个 n × n n times n n×n的图像,用 f × f f times f f×f 的过滤器做卷积,那么输出的维度就是 ( n − f + 1 ) × ( n − f + 1 ) ( n − f + 1 ) times ( n − f + 1 ) (n−f+1)×(n−f+1)。
- padding解决每一步输出缩小和图像边缘的大部分信息丢失问题
- padding:卷积操作之前对图像进行像素值为p的填充,则输出为 ( n + 2 p − f + 1 ) × ( n + 2 p − f + 1 ) ( n + 2 p − f + 1 ) times ( n + 2 p − f + 1 ) (n+2p−f+1)×(n+2p−f+1)。
- 选择填充多少像素,通常有两个选择,分别叫做Valid卷积和Same卷积:Valid卷积意味着不填充,Same卷积意味着填充后,输出大小和输入大小相同。
- 卷积步长 (Strided Convolutions):
- 再加入卷积步长s后,输出维度计算式为: ⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ left lfloorfrac{n + 2p - f}{s} + 1right rfloor times left lfloorfrac{n + 2p - f}{s} + 1right rfloor ⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋
- 注意:关于互相关和卷积的技术上理解,取决于数学教材or信号处理教材数学教科书,数学教科书上卷积的定义是过滤器镜像翻转(沿矩阵右上斜线),再元素乘积求和;按照机器学习的惯例,通常不进行翻转操作。从技术上说,这个操作可能叫做互相关更合适,但在深度学习文献中,按照惯例,我们将这(不进行翻转操作)也叫做卷积操作。
- 三维卷积 (Convolutions Over Volumes):
- 原图像: n × n × c h a n n e l s n times n times channels n×n×channels
- filter: f × f × c h a n n e l s f times f times channels f×f×channels(这两个通道数完全一样)
- output: ⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ × 1 left lfloorfrac{n + 2p - f}{s} + 1right rfloor times left lfloorfrac{n + 2p - f}{s} + 1right rfloor times 1 ⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋×1
- 单层卷积网络 (One Layer of a Convolutional Network):
- 原图像-> 多个不同的filter进行卷积得到多个输出-> 不同输出层增加各自的bias,再应用非线性激活函数得到输出结果-> (对应同一阶段的)输出层堆叠起来-> 最终得到 ⌊ n + 2 p − f s + 1 ⌋ × ⌊ n + 2 p − f s + 1 ⌋ × n f i l t e r left lfloorfrac{n + 2p - f}{s} + 1right rfloor times left lfloorfrac{n + 2p - f}{s} + 1right rfloor times n_{filter} ⌊sn+2p−f+1⌋×⌊sn+2p−f+1⌋×nfilter的矩阵
- 过滤器用 W [ ? ] {W}^{[?]} W[?]表示,原始输入为 a [ 0 ] {a}^{[0]} a[0]。(表示法完全类似于之前logistic逻辑回归内容所讲)
- 应用偏差和非线性函数之后,这一层的输出等于它的激活值 a [ l ] {a}^{[l]} a[l](即 n H [ l ] × n W [ l ] × n c [ l ] {n}_{H}^{[l]} times {n}_{W}^{[l]} times {n}_{c}^{[l]} nH[l]×nW[l]×nc[l])当你执行批量梯度下降或小批量梯度下降时,如果有 m 个例子,就是有 m 个激活值的集合,那么输出 A [ l ] = m × n H [ l ] × n W [ l ] × n c [ l ] {A}^{[l]} = m times {n}_{H}^{[l]} times {n}_{W}^{[l]} times {n}_{c}^{[l]} A[l]=m×nH[l]×nW[l]×nc[l]。
- 参数W为所有过滤器的集合再乘以过滤器的总数量: f [ l ] × f [ l ] × n c [ l − 1 ] × n c [ l ] {f}^{[l]} times {f}^{[l]} times {n}_{c}^{[l - 1]} times {n}_{c}^{[l]} f[l]×f[l]×nc[l−1]×nc[l]。
- 池化层 (Pooling Layers):除了卷积层,卷积网络也经常使用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性
- max pooling
注意区分max pooling(最大值池化)和卷积核的操作区别:池化作用于图像中不重合的区域(这与卷积操作不同) - average pooling
- max pooling
- 使用卷积的优点:和只用全连接层相比,卷积层的两个主要优势在于参数共享和稀疏连接
- 参数共享:观察发现,特征检测如垂直边缘检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域
- 稀疏连接:输出的某个像素值只取决于与filter相同大小的输入区域的像素值情况,其它像素值都不会对输出产生任影响。
经典网络
- 几个经典的神经网络结构:
详见:https://blog.csdn.net/weixin_36815313/article/details/105778993- LeNet-5:valid卷积-平均池化-valid卷积-平均池化-全连接层-全连接层-softmax输出
(此中使用的是sigmod函数和tanh函数,这种网络结构的特别之处在于各网络层之间有关联) - AlexNet:valid卷积-最大池化-same卷积-最大池化-再连续三次same卷积-最大池化-连续两个全连接层-softmax输出
(AlexNet比LeNet表现更为出色的另一个原因是它使用了ReLu激活函数) - VGGNet:
(VGG-16的这个数字16,就是指在这个网络中包含16个卷积层和全连接层。确实是个很大的网络,总共包含约1.38亿个参数,即便以现在的标准来看都算是非常大的网络。但VGG-16的结构并不复杂,而且这种网络结构很规整,都是几个卷积层后面跟着可以压缩图像大小的池化层,池化层缩小图像的高度和宽度。同时,卷积层的过滤器数量变化存在一定的规律,由64翻倍变成128,再到256和512。作者可能认为512已经足够大了,所以后面的层就不再翻倍了。无论如何,每一步都进行翻倍,或者说在每一组卷积层进行过滤器翻倍操作,正是设计此种网络结构的另一个简单原则。这种相对一致的网络结构对研究者很有吸引力,而它的主要缺点是需要训练的特征数量非常巨大。)
- LeNet-5:valid卷积-平均池化-valid卷积-平均池化-全连接层-全连接层-softmax输出
- 残差网络 (Residual Networks (ResNets)):
- 非常非常深的神经网络是很难训练的,因为存在梯度消失和梯度爆炸问题。跳跃连接(Skip connection)可以从某一层网络层获取激活,然后迅速反馈给另外一层,甚至是神经网络的更深层。可以利用跳跃连接构建能够训练深度网络的ResNets。
如果我们使用标准优化算法训练一个普通网络,比如说梯度下降法,或者其它热门的优化算法。如果没有残差,没有这些捷径或者跳跃连接,凭经验你会发现随着网络深度的加深,训练错误会先减少,然后增多。而理论上,随着网络深度的加深,应该训练得越来越好才对。但实际上,如果没有残差网络,对于一个普通网络来说,深度越深意味着用优化算法越难训练,随着网络深度的加深,训练错误会越来越多。
但有了ResNets就不一样了,即使网络再深,训练的表现却不错,比如说训练误差减少。这种方式确实有助于解决梯度消失和梯度爆炸问题,让我们在训练更深网络的同时,又能保证良好的性能。也许从另外一个角度来看,随着网络越来深,网络连接会变得臃肿,但是ResNet确实在训练深度网络方面非常有效。 - 残差块(Residual block)
- 残差块插入的时机是在线性激活之后,ReLU激活之前。
- “跳跃连接”,就是指 a [ l ] {a}^{[l]} a[l]跳过一层或者好几层,从而将信息传递到神经网络的更深层(之所以能实现跳跃连接是因为same卷积保留了维度)。
- 不太理解resnets不影响网络表现的原因:https://blog.csdn.net/weixin_36815313/article/details/105779620
- 残差网络起作用的主要原因是这些残差块学习恒等函数非常容易
- 普通网络和ResNets网络常用的结构是:卷积层-卷积层-卷积层-池化层-卷积层-卷积层-卷积层-池化层……依此重复。直到最后,有一个通过softmax进行预测的全连接层。
- 非常非常深的神经网络是很难训练的,因为存在梯度消失和梯度爆炸问题。跳跃连接(Skip connection)可以从某一层网络层获取激活,然后迅速反馈给另外一层,甚至是神经网络的更深层。可以利用跳跃连接构建能够训练深度网络的ResNets。
- 网络中的卷积及1x1卷积 (Network in Network and 1x1 Convolutions):
- 1×1卷积可以压缩通道数量(当然也可保持或增加)并减少计算
- 谷歌 Inception 网络简介 (Google Inception Network Motivation):
- Inception模块:使输出与输入长宽维度相同的,多种不同的过滤器( 1 ∗ 1 , 3 ∗ 3 , 5 ∗ 5 1*1,3*3,5*5 1∗1,3∗3,5∗5,max pooling)进行计算后,将各自的输出堆叠起来形成该模块。
- Inception网络不需要人为决定使用哪个过滤器或者是否需要池化,而是由网络自行确定这些参数,你可以给网络添加这些参数的所有可能值,然后把这些输出连接起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
- 如果你在构建神经网络层的时候,不想决定池化层是使用1×1,3×3还是5×5的过滤器,那么Inception模块就是最好的选择。我们可以应用各种类型的过滤器,只需要把输出连接起来。
- 计算成本问题:通过使用1×1卷积来构建瓶颈层,从而大大降低计算成本(先利用1*1卷积缩小网络,再用其它filter扩大网络,只要合理构建瓶颈层,既可以显著缩小表示层规模,又不会降低网络性能,从而节省了计算)。
- 以上内容结合构建inception网络详见:https://blog.csdn.net/weixin_36815313/article/details/105780151
- Inception网络的一个细节,它确保了即便是隐藏单元和中间层也参与了特征计算,它们也能预测图片的分类,在Inception网络中,起到一种调整的效果,并且能防止网络发生过拟合。
- 迁移学习
- 当手头的训练集很小时:
- 可以从网络上下载相似的开源实现(代码和权重),去掉最后的softmax层,根据需要创建自己的softmax层并利用自己的数据只对它进行训练。
- 下载代码后,由于前面的层都冻结了,相当于一个固定的函数,不需要改变。取训练集中的输入图像X,然后把它映射到softmax的前一层的激活函数,计算出这一层的特征或者激活值然后把它们存到硬盘里。(相当于神经网络的前部分,也即softmax层之前的所有层,视为一个固定映射),然后在此之上训练softmax分类器。所以,存储到硬盘或者说预计算方法的优点就是不需要每次遍历训练集再重新计算这个激活值。
- 如果有越来越多的数据,需要冻结的层数就越少,能够训练的层数就越多。这个理念就是,如果你有一个更大的数据集,也许有足够多的数据,那么不要单单训练一个softmax单元,而是考虑训练中等大小的网络,包含你最终要用的网络的后面几层。
- 当手头的训练集很小时:
对象检测(object detection)
- 目标定位 (Object Localization)
-
定位分类问题概念:不仅要用算法判断图片中是不是一辆汽车,还要在图片中标记出它的位置,用边框或红色方框把汽车圈起来,这就是定位分类问题。分类定位问题,通常只有一个较大的对象位于图片中间位置,对它进行识别和定位。而在对象检测问题中,图片可以含有多个对象,甚至单张图片中会有多个不同分类的对象。因此,图片分类(image classification)的思路可以帮助学习分类定位(classification with localization),而目标定位的思路又有助于学习目标检测(detection)
-
以构建汽车自动驾驶系统为例:
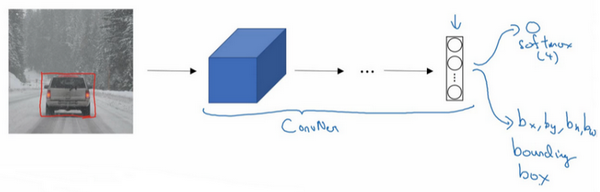
- 对象可能包括以下几类:行人、汽车、摩托车和背景,这四个分类就是softmax函数可能输出的结果。
- 定位图片中汽车的位置,可以让神经网络多输出几个单元(从而达到输出边界框的结果): b x , b y , b h , b w b_{x},b_{y},b_{h},b_{w} bx,by,bh,bw。约定图片左上角的坐标为(0,0),右下角标记为(1,1)。要确定边界框的具体位置,需要指定红色方框的中心点,这个点表示为 ( b x , b y ) (b_{x},b_{y}) (bx,by),边界框高宽分别为后两个参数。
- 训练集不仅包含神经网络要预测的对象分类标签,还要包含表示边界框的这四个数字(等等),接着采用监督学习算法,输出一个分类标签,还有四个参数值(等等),从而给出检测对象的边框位置(及其他信息)。
-
(承接上述例子)监督学习任务定义目标标签y:
-
y
=
[
p
c
b
x
b
y
b
h
b
w
c
1
c
2
c
3
]
y = begin{bmatrix}p_{c} \b_{x} \b_{y} \b_{h} \b_{w} \c_{1} \c_{2} \c_{3} end{bmatrix}
y=⎣
⎡pcbxbybhbwc1c2c3⎦
⎤
- p c p_{c} pc表示是否含有对象。如果对象属于前三类(行人、汽车、摩托车),则 p c = 1 p_{c}=1 pc=1,否则为0, p c = 0 p_{c}=0 pc=0时不关心后续结果输出。
- c 1 , c 2 , c 3 c_{1},c_{2},c_{3} c1,c2,c3表示该对象属于1-3类中的哪一类,是行人,汽车还是摩托车1。
- 损失函数:
- 采用平方误差(一种简化描述):
y 1 = p c = 1 : L ( y ^ , y ) = ( y ^ 1 − y 1 ) 2 + . . . + ( y ^ 8 − y 8 ) 2 y_{1} = p_{c} = 1: L(hat{y},y) = (hat{y}_{1} - y_{1})^{2} + ... + (hat{y}_{8} - y_{8})^{2} y1=pc=1:L(y^,y)=(y^1−y1)2+...+(y^8−y8)2
y 1 = p c = 0 : L ( y ^ , y ) = ( y ^ 1 − y 1 ) 2 y_{1} = p_{c} = 0: L(hat{y},y) = (hat{y}_{1} - y_{1})^{2} y1=pc=0:L(y^,y)=(y^1−y1)2 - 实际应用中,对于 c 1 , c 2 , c 3 c_{1},c_{2},c_{3} c1,c2,c3的softmax输出可以用之前学softmax时的带log的损失函数,对 p c p_{c} pc用逻辑回归的损失函数(平方差也可以),对b的四个参数用平方差或其他类似方法。
- 采用平方误差(一种简化描述):
-
y
=
[
p
c
b
x
b
y
b
h
b
w
c
1
c
2
c
3
]
y = begin{bmatrix}p_{c} \b_{x} \b_{y} \b_{h} \b_{w} \c_{1} \c_{2} \c_{3} end{bmatrix}
y=⎣
⎡pcbxbybhbwc1c2c3⎦
⎤
-
- 目标点检测:
- 神经网络可以通过输出图片上特征点的 ( x , y ) (x,y) (x,y)坐标来实现对目标特征的识别。
- 举栗:
- 人脸识别:可以让神经网络最后一层输出四个眼角的坐标等等特征点,假设脸部有64个特征点。选定特征点个数,并生成包含这些特征点的标签训练集(图片特征点x和y标签的集合,这些点都是人为辛苦标注的),然后训练好后就可以利用神经网络输出脸部关键特征点的位置。
具体做法是,准备一个卷积网络和一些特征集,将人脸图片输入卷积网络,输出1或0,1表示有人脸,0表示没有人脸,然后输出 ( l 1 x , l 1 y ) . . . ( l 64 x , l 64 y ) (l_{1x},l_{1y})...(l_{64x},l_{64y}) (l1x,l1y)...(l64x,l64y),l代表一个特征。 - 人体姿态检测:可以定义一些关键特征点,如胸部的中点,左肩,左肘,腰等等。
- 注意特征点的顺序在所有图片中必须保持一致。如:特征点1始终是右眼的外眼角,特征点2是右眼的内眼角…
- 人脸识别:可以让神经网络最后一层输出四个眼角的坐标等等特征点,假设脸部有64个特征点。选定特征点个数,并生成包含这些特征点的标签训练集(图片特征点x和y标签的集合,这些点都是人为辛苦标注的),然后训练好后就可以利用神经网络输出脸部关键特征点的位置。
- 卷积网络实现对象检测(基于滑动窗口的目标检测算法)
以构建汽车检测算法为例-
基本思路:
- 训练好对应的分类卷积网络:创建一个标签训练集,样本中的正样本可以使用适当剪切的图片(整张图片几乎都被汽车占据)。有了标签训练集后训练卷积网络,输入这些适当剪切过的图片,卷积网络输出y,0或1表示图片中有汽车或没有汽车。
- 滑动窗口目标检测实现:基于朴素的第一直觉,我们的想法应该是这个鸭子
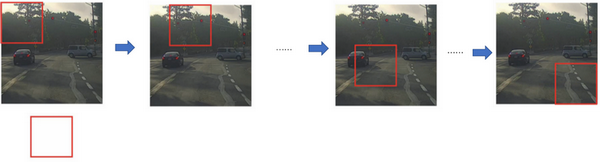
这个特定大小的窗口以特定步长进行滑动,每次截出的区域再输入给训练好的卷积神经网络处理(输出0 or 1)。
3. 这种算法以某个步幅滑动这些方框窗口遍历整张图片,对这些方形区域进行分类,判断里面有没有汽车。有很明显的缺点,就是计算成本,在图片中剪切出太多小方块,卷积网络要一个个地处理:选用的步幅大,粗糙间隔尺寸可能会影响性能,小步幅传递给卷积网络的小窗口会特别多,计算成本高。 -
改进:滑动窗口的卷积实现
-
先导:全连接层(FC)转化为卷积层(直接上图很好理解,注意开始为16个553的filter)
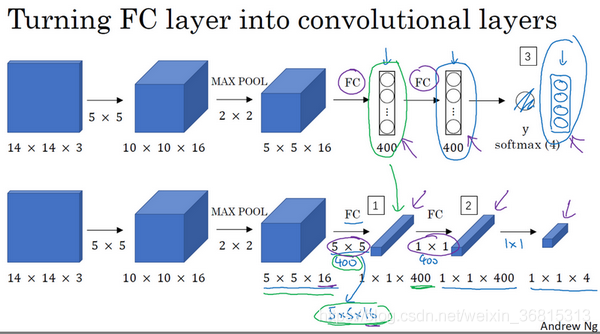
-
假设输入给卷积网络的图片大小是14×14×3,测试集图片是16×16×3,在最初的滑动窗口算法中,蓝色区域输入卷积网络生成0或1分类。接着向右滑动2个像素,将这个绿框区域输入给卷积网络,得到另外一个标签0或1…。卷积网络共运行了4次,最终输出4个标签。
结果发现,这4次卷积操作中很多计算都是重复的。这4次前向传播过程中共享很多计算(尤其操作1:卷积网络运行同样的参数,使得相同的5×5×16过滤器进行卷积操作,得到12×12×16的输出层,2操作的重复计算同理)…应用400个5×5的过滤器(编号3),得到2×2×400的输出层…最终得到2×2×4的输出层。在输出层这4个子方块中,蓝色的是图像左上部分14×14的输出(红色箭头标识),右上角方块是图像右上部分(绿色箭头标识)的对应输出…(后面同理,具体计算步骤可以自己推理一下)。
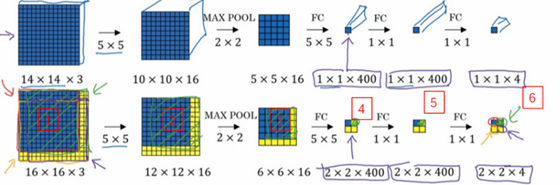
所以不需要把输入图像分割成四个子集,分别执行前向传播,而可以把它们作为一张图片输入给卷积网络进行计算,但此算法仍然存在边界框的位置可能不够准确的问题。
-
-
- Bounding Box预测
-
YOLO算法(You only look once):
-
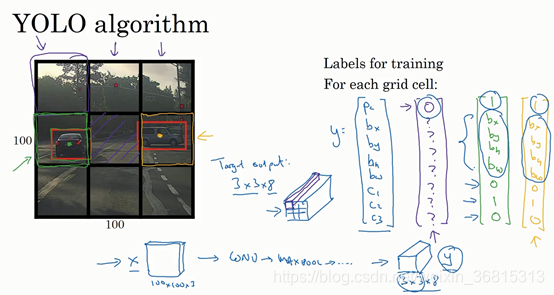
在图像上放一个网格(为便于理解采用3×3网格,实际实现时会用更精细的网格,可能是19×19),基本思路是将图像分类和定位算法应用到9个格子上。
-
关于训练集数据的标签:对一张图片的九个格子,每格指定一个y(就如之前在分类和定位算法提到的一样,是8×1的向量)2。所以对于9个格子中任何一个都会得到一个8维输出向量,总的输出尺寸是3×3×8。
- 算法的优点在于神经网络可以输出精确的边界框,且运行速度很快,可以达到实时识别。只要每个格子中对象数目没有超过1个,算法应该是没问题的,实践中使用更精细的网格,多个对象分配到同一个格子得概率就更小。
-
-
编码 b x , b y , b h , b w b_{x},b_{y},b_{h},b_{w} bx,by,bh,bw注意的细节:
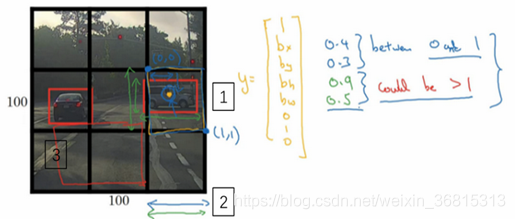
在YOLO算法中,对于编号1所示方框,约定左上,右下点分别为 ( 0 , 0 ) , ( 1 , 1 ) (0,0),(1,1) (0,0),(1,1)。 b x , b y , b h , b w b_{x},b_{y},b_{h},b_{w} bx,by,bh,bw单位是相对于格子尺寸的比例,所以 b x , b y b_{x},b_{y} bx,by必须在0和1之间,从定义上看,中点位于对象分配到格子的范围内,如果不在0和1之间,这个对象就应该分配到另一个格子上。 b h , b w b_{h},b_{w} bh,bw可能会大于1。指定边界框的方式有很多,但这种约定比较合理,YOLO的研究工作有其他参数化的方式,可能效果会更好。
-
- 交并比(IoU: Intersection over Union)与非极大抑制()
- 交并比概念:
在对象检测任务中,交并比函数是计算两个边界框(定位对象的实际边界框与算法给出的边界框)所围交集和并集区域面积之比。一般约定,在计算机检测任务中,IoU≥0.5则结果可以接受。交并比是衡量定位精确度的一种方式, - 非极大抑制:
-
目前为止学到的对象检测中还有一个问题:算法可能对同一个对象做出多次检测(YOLO方法中第一次对图片划分时格子太密会出现这个情况)。非极大值抑制这个方法可以确保你的算法对每个对象只检测一次。
-
原理:每次报告每个检测结果有相关的概率 p c p_{c} pc(实际上应该可能是 p c p_{c} pc乘上 c 1 c_{1} c1或 c 2 c_{2} c2或 c 3 c_{3} c3),找出其中概率最大的并抑制/剔除其他的。
-
简例:

首先在19×19网格上执行算法,得到19×19×8的输出尺寸。我们简化一下只做汽车检测,去掉 c 1 , c 2 , c 3 c_{1},c_{2},c_{3} c1,c2,c3,每个格子输出变成了五维向量。先去掉所有 p c < = 0.6 p_{c}<=0.6 pc<=0.6的边界框,再从剩下的边界框里一直选择概率最高的,然后把它输出成预测结果,再去掉所有剩下的边界框(包括和已确定输出边界框有高重叠面积——很高交并比的边界框全部抛弃)。
-
例子只介绍了算法检测单个对象的情况,如果尝试同时检测三个对象,比如说行人、汽车、摩托,那么输出向量就会有三个额外的分量。独立进行三次非极大值抑制,对每个输出类别都做一次即可。
-
- 交并比概念:
- Anchor Boxes
-
导入:到目前为止,对象检测中还存在每个格子只能检测出一个对象不能检测出多个对象的问题(如果一个格子有多个对象,按之前的方法最终只能输出一个框),使用anchor box可以一定程度改进上述问题。
-
原理:将预定义的anchor box与预测结果关联起来,标签不再是8维的,变成了预定的anchor box数量 × 8维的。
-
简例:
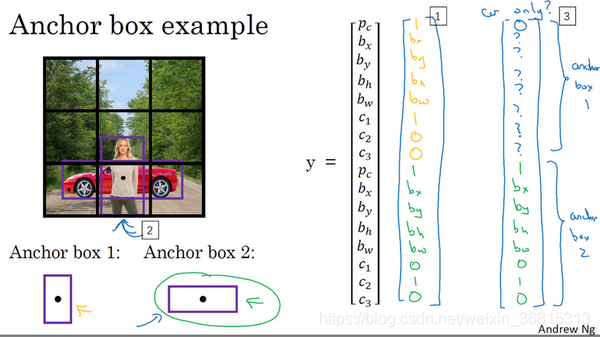
如图,anchor box1关联标签的前八个参数(关于车子),box2关联后八个(关于人),一个格子的输出变成了16维。在编号2的格子中(有人有车),对于人这一对象,外形更像anchor box1,而车外形更像anchor box2,所以这个格子的标签书写就如图编号1所示;又有其中一个格子有一辆车没有行人,则因为对象外形更像anchor box2,输出标签如图编号3所示。
-
仍未解决的问题:如果设置有两个anchor box,但在同一个格子中有三个对象,这种情况算法处理不好;两个对象都分配到一个格子中,而且它们的anchor box形状也一样,这是算法处理不好的另一种情况(其实出现的情况不多,所以对性能的影响应该不会很大)。
-
建立anchor box这个概念,是为了处理两个对象出现在同一个格子的情况,实践中这种情况很少发生,特别是如果用19×19网格而不是3×3的网格,两个对象中点处于361个格子中同一个格子的概率很低,也许设立anchor box的好处在于anchor box能让学习算法能够更有针对性,特别在数据集有一些很高很瘦的对象,比如说行人,还有像汽车这样很宽的对象。人们一般手工指定anchor box形状,可以选择5到10个anchor box形状,覆盖到多种不同的形状。3
-
- 候选区域
- 滑动窗法:使用训练过的分类器对一张图片进行滑动检测,此算法会在显然没有任何对象的区域浪费时间
- R-CNN算法:带区域的卷积网络/CNN。此算法尝试选出一些区域(比如图像分割算法),在这些区域上运行卷积网络分类器,如下图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Gkf9RmBJ-1658742975151)(图像分割.png)]- 注意,R-CNN算法不会直接信任输入的边界框,它也会输出一个边界框( b x , b y , b h , b w b_{x},b_{y},b_{h},b_{w} bx,by,bh,bw),这样得到的边界框更精确,比单纯使用图像分割算法给出的色块边界要好。
- R-CNN因为采用的是滑动窗法,运行比较慢。
- 改进R-CNN:
- Fast R-CNN:滑动窗法变卷积实现,但是得到候选区域的聚类步骤仍然比较慢
- Faster R-CNN(又是何凯明):候选区域色块划分用卷积神经网络实现
卷积神经网络的特殊应用
人脸识别系统
-
现在普及的人脸识别系统,包含人脸识别+活体检测(可用监督学习实现)两个部分
-
人脸识别部分介绍
- 人脸验证:
- 输入为image+ID/name
- 输出为是否信息匹配(这个人的图片和声称的信息相符)
- 这是一种1对1问题
- 人脸识别:
- 比验证更难,对系统的性能,准确率要求更高
- 有K个人的database(数据库)
- 输入为一张图片
- 输出这张图片匹配的ID/name(在K人之中)
- 人脸验证:
人脸识别系统构造
- One-Shot 学习
- 人脸识别的困难:比如在员工数据库中,每个员工可能只有一张照片。如果利用卷积神经网络实现,用softmax单元来输出n+1个标签(n对应数据库中员工个数,+1这一项表示不是这n个人的概率),这样效果不好,因为训练集很小,且有新成员加入数据库后,网络softmax层又要变化,需要重新训练。
- 解决方法:让人脸识别做到一次学习。神经网络需要学习这样一个函数
d
(
i
m
g
1
,
i
m
g
2
)
=
d
e
g
r
e
e
−
o
f
−
d
i
f
f
e
r
e
n
c
e
−
b
e
t
w
e
e
n
−
i
m
a
g
e
s
d(img1,img2)=degree-of-difference-between-images
d(img1,img2)=degree−of−difference−between−images,
- 两张图片为输入
- 输出这两张图片的差异值
- 如果是同一个人的两张照片,网络输出很小的值;如果是两个长相差别很大的人的照片,输出很大的值。所以在识别过程中,如果两张图片差异值小于阈值 τ tau τ(超参数),就能预测这两张图片是同一个人;如果差异值大于 τ tau τ,就能预测这是不同的两个人。
-
Siamese Network
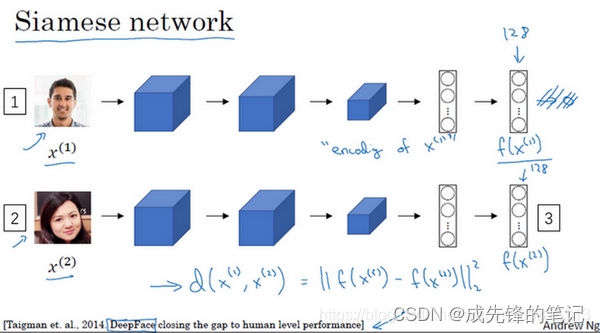
- 实现d函数功能的一个方法就是使用siamese网络,如上图
- 图示的上下两个卷积神经网络完全一致,最后通过全连接得到的是特征向量(我们把最后的128维向量称为encoding<编码>,不再设置softmax)
- 最后定义 d ( x ( 1 ) , x ( 2 ) ) = ∣ ∣ f ( x ( 1 ) ) − f ( x ( 2 ) ) ∣ ∣ 2 d(x^{(1)}, x^{(2)}) = || f(x^{(1)}) - f(x^{(2)}) ||^{2} d(x(1),x(2))=∣∣f(x(1))−f(x(2))∣∣2 4
- 对于两个不同的输入,运行相同的卷积神经网络,然后比较它们,这一般叫做Siamese网络架构
- siamese网络的训练,实际上只是训练一个网络
- Siamese Network之Triplet Loss
通过学习神经网络的参数来得到优质的人脸图片编码,方法之一就是定义三元组损失函数然后应用梯度下降
- 为使用三元组损失,一次比较需要有三张图片(Anchor图片、Positive图片、Negative图片)A,P,N。A和P(positive就意味着是同一个人)是同一个人的不同照片,N是另一个人的照片。
- 用公式表示,自然希望有
∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 ≤ ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 || f(A) - f(P) ||^{2} le || f(A) - f(N) ||^{2} ∣∣f(A)−f(P)∣∣2≤∣∣f(A)−f(N)∣∣2
也即 d ( A , P ) − d ( A , N ) ≤ 0 d(A,P) - d(A,N) le 0 d(A,P)−d(A,N)≤0
但是会有 0 − 0 ≤ 0 0 - 0 le 0 0−0≤0的情况,为了避免这种情况发生,引入margin间隔: α alpha α
∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 + α ≤ 0 || f(A) - f(P) ||^{2} - || f(A) - f(N) ||^{2} + alpha le 0 ∣∣f(A)−f(P)∣∣2−∣∣f(A)−f(N)∣∣2+α≤0 - 三元组损失函数:基于三张图片A,P,N
L ( A , P , N ) = m a x ( ∣ ∣ f ( A ) − f ( P ) ∣ ∣ 2 − ∣ ∣ f ( A ) − f ( N ) ∣ ∣ 2 + α , 0 ) L(A,P,N) = max(|| f(A) - f(P) ||^{2} - || f(A) - f(N) ||^{2} + alpha, 0) L(A,P,N)=max(∣∣f(A)−f(P)∣∣2−∣∣f(A)−f(N)∣∣2+α,0)- 当max左项小于等于零,达到了我们想要的目标,故损失为0;max左项大于零,最终得到一个正的损失值。
- 最小化L的结果就是让max左项小于等于0.
- 代价函数
J = ∑ i = 1 m L ( A ( i ) , P ( i ) , N ( i ) ) J = sum_{i=1}^{m} L(A^{(i)}, P^{(i)}, N^{(i)}) J=i=1∑mL(A(i),P(i),N(i))- 整个网络代价函数为每一组三元组损失之和, i表示第i组数据
- 关于训练集:
- 需要有同一个人的多张不同照片组成一个个三元组(A,P,N)
- 注意N不能随机选,因为随机选择下的 d ( A , P ) − d ( A , N ) + α ≤ 0 d(A,P) - d(A,N) + alpha le 0 d(A,P)−d(A,N)+α≤0很容易达到,这样训练网络梯度算法没什么效果,最终网络很轻松能达到结果,并不能学到什么。故要制作难训练的三元组,也即使 d ( A , P ) d(A,P) d(A,P)尽量接近 d ( A , N ) d(A,N) d(A,N)
- Siamese Network变体之面部验证与二分类
另一训练神经网络的方法是选取一对神经网络(Siamese),使其同时计算这些embeddings(嵌入),比如128维的嵌入/更高维,然后将其输入到逻辑回归单元进行预测,如果是相同的人则输出是1,若是不同的人,输出是0。这就把人脸识别问题转换为一个二分类问题,训练这种系统时可以替换Triplet loss的方法。
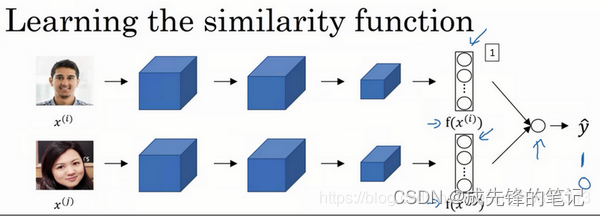
- y ^ = σ ( ∑ k = 1 128 w k ∣ f ( x ( i ) ) k − f ( x ( j ) ) k ∣ + b ) hat{y} = sigma( sum_{k=1}^{128} w_{k}|f(x^{(i)})_{k} - f(x^{(j)})_{k}| + b) y^=σ(k=1∑128wk∣f(x(i))k−f(x(j))k∣+b)
- 上式中 ∣ f ( x ( i ) ) k − f ( x ( j ) ) k ∣ |f(x^{(i)})_{k} - f(x^{(j)})_{k}| ∣f(x(i))k−f(x(j))k∣可替换为 χ 2 = ( f ( x ( i ) ) k − f ( x ( j ) ) k ) 2 f ( x ( i ) ) k + f ( x ( j ) ) k chi^{2} = frac{(f(x^{(i)})_{k} - f(x^{(j)})_{k})^{2}}{f(x^{(i)})_{k} + f(x^{(j)})_{k}} χ2=f(x(i))k+f(x(j))k(f(x(i))k−f(x(j))k)2
- 在实际部署时,可以预先计算每个员工对应的编码,当某一员工走近时可以使用上方卷积网络计算编码,再与预先计算好的编码比较输出预测值。这种预训练的工作也可以用在triplet loss函数上。
- 总结:把人脸验证当作一个监督学习,创建一个只有成对图片的训练集,目标标签是1表示一对图片是一个人,目标标签是0表示图片中是不同的人。利用不同的成对图片,使用反向传播算法去训练得到Siamese神经网络。
- 术语补充
解释来源知乎:https://www.zhihu.com/question/507322595/answer/2286602597
- encoder 编码器,将信息进行编码(一般是向量化或降维,如词向量)并保持语义信息(encoder的学习方向)
- embedding一般指映射得到的向量,直观含义就是将某种人类能理解的模态数据(如文本、图片),转换为计算机能够处理的向量,这一过程通常称为embed(嵌入)。embedding在不同任务下会有具体的指代:
- 在NLP中,一般会称encoder的结果是embedding
- 在ViT中,称Transformer前,对图像Patch进行特征提取的结果称为embedding。
- decoder 解码器,将特征向量解码为任务相关的输出。如词向量->词,feature map->检测框+类别序列。
- 总体来说,encoder用来提取、凝练(降维)特征,embedding指由某种能理解的模态提取得到的特征,decoder用于将特征向量转化为我们需要的结果。
神经风格迁移
- 效果展示

- 深度卷积网络可视化理解
加入了自己的理解和一些表达,没有去看论文原文,如有错误欢迎批评指正
假如有训练好的卷积神经网络,观察各隐藏层中隐藏单元的计算结果:
- 第一隐藏层有很多隐藏单元。我们遍历一遍数据集找到使这一层的某一个特定单元激活值最大的图片块,发现这些图片块都具有垂直线条的画面(只是举个例子),说明第一层的这个单元对图片中固定区域内的垂直线条“敏感”。
-
为什么我认为是固定区域?可以从卷积的过程去分析,随着卷积深度加深,深层隐藏层内的单元对应最初图片的区域会越来越大(后面会提到)。貌似这个固定区域有官方说法叫感受野(Receptive Field)
- 同理,这个第一层中的其他隐藏单元可能会对其它线条类型(如左斜线等等)“敏感”。以此类推,可以这样理解,第一层的隐藏单元通常会找一些简单的特征,比如说边缘或者颜色阴影。
- 如果在深层的隐藏单元中进行计算,卷积神经网络的深层部分,一个隐藏单元会看到一张图片更大的视野,检测的模式和特征也就更复杂。
- (极端情况下,可以假设每一个像素都会影响到神经网络更深层的输出)
- 再去考虑:CNN中filter也有自己的数量,如 5 ∗ 5 ∗ 3 ∗ 12 5*5*3*12 5∗5∗3∗12中的12,就是要对前一层某一特定区域进行12次卷积,可能得到对这一特定区域的12次不同特点的提取。后续风格代价部分也会具体举例描述。
- 神经风格迁移算法概要
构建一个神经风格迁移系统关键需要定义其代价函数,再梯度下降法对代价函数最小化。
- 定义:内容图像C(content),风格图片S(style),生成新图片G(generate)
- 代价函数 = 内容代价函数(度量C和G的相似度) + 风格代价函数(度量S和G的相似度)
J ( G ) = α J c o n t e n t ( C , G ) + β J s t y l e ( S , G ) J(G) = alpha J_{content}(C,G) + beta J_{style}(S,G) J(G)=αJcontent(C,G)+βJstyle(S,G)
α , β alpha , beta α,β为两个超参数,赋予两个代价一定的权重
- 算法运行流程:
- 随机初始化生成新图像G,比如100*100*3的图片(由于随机生成使得G就是一个白噪声图像–花屏)
- 使用代价函数 J ( G ) J(G) J(G)用梯度下降法逐步更新G图像的像素值,慢慢得到生成图片。

- 内容代价函数
- 选用隐藏层l计算内容代价:(包含了自己的一些理解)
- 如果l=1(浅层):代价函数不断最小化,会使生成图片非常非常接近内容图片
- 如果l为深层:生成图片会确保与内容图片整体上有同样的要素(比如:图片上都含有一只狗)
- 实际中l的选择不会太深也不会太浅。
- J c o n t e n t ( C , G ) = 1 / 2 ∣ ∣ a [ l ] [ C ] − a [ l ] [ G ] ∣ ∣ 2 2 J_{content}(C,G) = 1/2 || a^{[l][C]} - a^{[l][G]} ||^{2}_{2} Jcontent(C,G)=1/2∣∣a[l][C]−a[l][G]∣∣22
- 1/2这个归一化影响不大,因为我们有超参数 α alpha α进行调整。
- 上式a表示层l的激活单元矩阵,计算的是做差后矩阵的L2范数的平方,也即各个差值的平方和。
- 风格代价函数
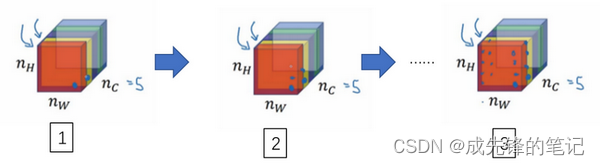
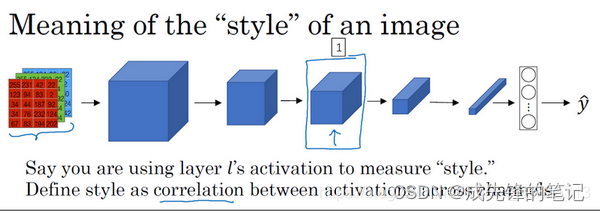
-
我们取出了某一隐藏层,为方便分析,假设这隐藏层有五个通道,我们需要关注任两个通道对应位置的激活项,并计算它们的相关系数。
-
一个通道是对某个特征的检测(因为生成该通道的filter参数确定),通道中某一处数值的强弱就是对当前特征强弱的反应
-
来看一个例子:

- 假设红色的通道(编号1)能找出图片中的特定位置是否含有这些垂直的纹理(编号3),而第二个黄色的通道(编号2)可以粗略地找出橙色的区域。
- 如果它们有高度相关性,那么这幅图片中出现垂直纹理的地方很大概率是橙色的;如果它们是不相关的,图片中有垂直纹理的地方很大概率不是橙色的。
- 相关系数描述的是线性相关关系,(由于是线性关系)直观上可以理解为当图片某处出现这种垂直纹理时,该处又同时是橙色的可能性。
-
相关系数提供了一种去测量这些不同的特征的方法,去测量它们在图片中的各个位置同时出现或不同时出现的频率。
-
如果我们在通道之间使用相关系数来描述通道的风格,我们需要测量生成图像中第一个通道(编号1)是否与第二个通道(编号2)相关,通过测量得知在生成的图像中垂直纹理和橙色同时出现或者不同时出现的频率,进而能够测量生成的图像的风格与输入的风格图像的相似程度。
-
公式描述
- 设 a i , j , k [ l ] a_{i,j,k}^{[l]} ai,j,k[l]表示网络中第l隐藏层中i(高度),j(宽度),k(通道)对应位置下的激活项。
- 需要计算风格矩阵 G [ l ] ( S ) , G [ l ] ( G ) G^{[l](S)}, G^{[l](G)} G[l](S),G[l](G),两者大小均为 n c h a n n e l s ∗ n c h a n n e l s n_{channels}*n_{channels} nchannels∗nchannels
- 以风格矩阵
G
[
l
]
G^{[l]}
G[l]中的某一个值计算为例(不在考虑是S图像的还是G图像的了,都一样):
- $ G^{[l]}_{kk’}$ 表示第k通道和第k’通道之间的对应位置上的激活项乘积之和
G k k ′ [ l ] = ∑ i = 1 n H [ l ] ∑ j = 1 n W [ l ] a i j k [ l ] a i j k ′ [ l ] G^{[l]}_{kk'} = sum_{i=1}^{n_{H}^{[l]}} sum_{j=1}^{n_{W}^{[l]}} a^{[l]}_{ijk} a^{[l]}_{ijk'} Gkk′[l]=i=1∑nH[l]j=1∑nW[l]aijk[l]aijk′[l] - $ G^{l}{kk’}, G^{l}{kk’} $ 的计算就是上述公式,进而得到 $ G^{l}, G^{l} $
- $ G^{[l]}_{kk’}$ 表示第k通道和第k’通道之间的对应位置上的激活项乘积之和
- 由此,有风格代价函数:
J s t y l e [ l ] ( S , G ) = 1 ( 2 n H [ l ] n W [ l ] n C [ l ] ) 2 ∣ ∣ G [ l ] ( S ) − G [ l ] ( G ) ∣ ∣ F 2 J_{style}^{[l]}(S,G) = frac{1}{(2n_{H}^{[l]}n_{W}^{[l]}n_{C}^{[l]})^{2}} || G^{[l](S)} - G^{[l](G)} ||_{F}^{2} Jstyle[l](S,G)=(2nH[l]nW[l]nC[l])21∣∣G[l](S)−G[l](G)∣∣F2- F角标表示矩阵的Frobenius范数, ∣ ∣ A ∣ ∣ F = ∑ i = 1 m ∑ j = 1 n a i j 2 ||A||_{F} = sqrt{sum_{i=1}^{m} sum_{j=1}^{n} a_{ij}^{2}} ∣∣A∣∣F=∑i=1m∑j=1naij2
- 另外, J s t y l e [ l ] ( S , G ) J_{style}^{[l]}(S,G) Jstyle[l](S,G)计算式前面那一堆归一化系数实际上也用不着,我们有超参数 $ beta $
- 若果要对网络各隐藏层都使用风格代价函数,会让结果变得更好:定义代价函数为,把各个层的风格代价函数结果乘以对应权重
λ
[
l
]
lambda^{[l]}
λ[l]再加起来。
J s t y l e ( S , G ) = ∑ l λ [ l ] J s t y l e [ l ] ( S , G ) J_{style}(S,G) = sum_{l} lambda^{[l]} J_{style}^{[l]}(S,G) Jstyle(S,G)=l∑λ[l]Jstyle[l](S,G)
- 一维到三维推广
- 我直接写两个式子,看看就懂了(注意,这里的*特指卷积,在其他地方出现的*还是乘的意思)
- 一维: ( 14 × 1 ) ∗ ( 5 × 1 × 16 ) − o u t p u t > ( 10 × 16 ) (14 times 1)*(5 times 1 times 16) -output> (10 times 16) (14×1)∗(5×1×16)−output>(10×16)
-
1表示通道数,16表示filter个数
- 二维: ( 14 × 14 × 1 ) ∗ ( 5 × 5 × 1 × 16 ) − o u t p u t > ( 10 × 10 × 16 ) (14 times 14 times 1)*(5 times 5 times 1 times 16) -output> (10 times 10 times 16) (14×14×1)∗(5×5×1×16)−output>(10×10×16)
- 三维: ( 14 × 14 × 3 × 1 ) ∗ ( 5 × 5 × 3 × 1 × 16 ) − o u t p u t > ( 10 × 10 × 3 × 16 ) (14 times 14 times 3 times 1)*(5 times 5 times 3 times 1 times 16) -output> (10 times 10 times 3 times 16) (14×14×3×1)∗(5×5×3×1×16)−output>(10×10×3×16)
再次注意我们假设图片中只含有一个对象 ↩︎
观察对象的中点,然后对象分配到其中点所在的格子,所以即使对象可以横跨多个格子,也只会被分配到9个格子其中之一,或者19×19网络的其中一个格子。在19×19网格中,两个对象的中点处于同一个格子的概率就会更低。 ↩︎
还有更高级的版本,后期YOLO论文中有更好的做法,k-平均算法,可以将两类对象形状聚类。 ↩︎
d实际上就是distance的意思 ↩︎
最后
以上就是细腻篮球最近收集整理的关于卷积神经网络的全部内容,更多相关卷积神经网络内容请搜索靠谱客的其他文章。








发表评论 取消回复