2015ACM/ICPC亚洲区上海站-重现赛 A - An Easy Physics Problem

题意：在二维平面上有一个圆,知道圆心坐标和半径，现在给你一个点A，并且给你一个有方向的速度矢量v，问你这个点能否在按给定的速度矢量方向前进后，最终能经过给出的另一个点B，你可以通过与圆的碰撞来改变点的运动方向，碰撞属于完全弹性碰撞

思路：

总共可以分为两种情况，第一种情况，点未碰撞前的运动轨迹与圆相切或相离，这种情况我们只需要判断B点是否在它的运动轨迹上就行了，第二种情况，点未碰撞前的运动轨迹与圆相交，这个时候我们将交点与圆心的连线作为对称轴，找出b点关于对称轴的对称点，然后以交点为起始点，按-v的方向前进，看b点的对称点是否在该运动轨迹上就行，需要注意精度问题。

首先我们来构思怎么判断是否有交点，有交点的话怎么把交点坐标找出来。

不妨设A点坐标为,圆心坐标为,速度矢量为

可列点的运动方程为

圆的方程为

将点的运动方程代入到圆的方程中去可以得到

通过的值来判断是否相交，若相交的话则求出t的值，然后求出交点坐标

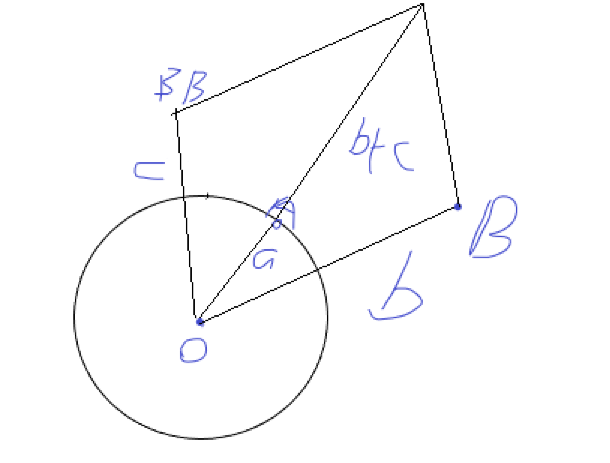
已知O，A，B的坐标，BB的坐标是我们待求的

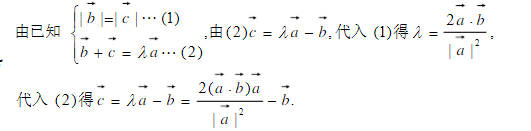
由可以求得BB的坐标

求得BB坐标后，按-v的方向前进，看BB是否在该运动轨迹上就行

代码：

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define ll long long
#define eps 1e-6
const int maxn=1e5+9;
int dcmp(double x){
    if(fabs(x)<eps)return 0;
    else if(x<0)return -1;
    else return 1;
}
struct Point{
    double x,y;
    Point(){

    }
    Point(double x, double y): x(x), y(y) {}
    Point operator + (const Point &a)const{
        return Point(x+a.x,y+a.y);
    }
    Point operator -(const Point &a)const{
        return Point(x-a.x,y-a.y);
    }

    void read(){
        scanf("%lf%lf",&x,&y);
    }
}a,b,v;
Point operator *(double t,Point a){
        return Point(a.x*t,a.y*t);
}
struct Circle{
    double r;
    Point c;
    void read(){
        c.read();
        scanf("%lf",&r);
    }
}cir;
struct Line{
    Point p,v;
    Line(Point p, Point v): p(p.x, p.y), v(v.x, v.y) {}
    Point point(double t){
        return p+t*v;
    }
};
inline double pow2(double x){
    return x*x;
}
int getLineCircleIntersection(Line L,Circle C,Point&pt){
    double t;
    double a=pow2(L.v.x)+pow2(L.v.y);
    double b=2*((L.p.x-C.c.x)*L.v.x+(L.p.y-C.c.y)*L.v.y);
    double c=pow2(L.p.x-C.c.x)+pow2(L.p.y-C.c.y)-pow2(C.r);
    double deta=b*b-4*a*c;
    if(dcmp(deta)<=0)return 0;
    else {
        t=(-b-sqrt(deta))/(2*a);
        if(dcmp(t)>0){
        pt=L.point(t);
        return 1;
        }
        return 0;
    }
}

double Dot(Point v1,Point v2){//向量点乘
    return v1.x*v2.x+v1.y*v2.y;
}
double Cross(Point v1,Point v2){//向量叉乘
    return v1.x*v2.y-v1.y*v2.x;
}
bool det(Point v1,Point v2){
    if(fabs(Cross(v1,v2))<eps)return true;
    return false;
}
bool SameLine(Point v1,Point v2){//判断两向量是否平行
    if(det(v1,v2))return true;
    return false;
}
Point GetSymmetricPoint(Point O,Point A,Point B){
    Point a=A-O;//对称轴的向量形式
    Point b=B-O;//点关于对称轴起点的连线的向量形式
    return 2*(O+Dot(a,b)/Dot(a,a)*a)-B;//返回对称点
}
double dist(Point a,Point b){//两点间的距离
    return hypot(a.x-b.x,a.y-b.y);
}
int main(){
    int i,j,k,n,t;
    scanf("%d",&t);
    for(int c=1;c<=t;c++){
        cir.read();a.read();v.read();b.read();
        Point pt;
        Line L(a,v);
        int flag=getLineCircleIntersection(L,cir,pt);
        printf("Case #%d: ",c);
        if(flag){
            if(SameLine(v,b-a)&&dist(a,b)<dist(a,pt)+eps)printf("Yesn");
            else{
                Point symb=GetSymmetricPoint(cir.c,pt,b);
                if(SameLine(Point(-v.x,-v.y),symb-pt))printf("Yesn");
                else printf("Non");
            }
        }
        else{
            if(SameLine(v,b-a))printf("Yesn");
            else{
                printf("Non");
            }
        }
    }
}

最后

以上就是大力鸡翅为你收集整理的2015ACM/ICPC亚洲区上海站-重现赛 A - An Easy Physics Problem的全部内容，希望文章能够帮你解决2015ACM/ICPC亚洲区上海站-重现赛 A - An Easy Physics Problem所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。