第一章 基本知识
一、数字信号与数字系统
1. 数字信号
- 人们习惯将连续量称为模拟量,表示模拟量的信号称作连续信号。
- 若信号的变化在时间上和数值上都是离散的,或者说断续的,则称为离散信号。
离散信号的变化可以用不同的数字反映,所以又称为数字信号,简称为数字量。
2. 数字系统
- 数字系统是一个能对数字信号进行加工、传递、存储的实体,它由实现各种功能的数字逻辑电路相互连接而成。
- 用来处理数字信号的电子线路称为数字电路。由于数字电路的各种功能是通过逻辑运算和逻辑判断来实现的,所以数字电路又称为数字逻辑电路或者逻辑电路。
3. 数字逻辑电路
1)数字逻辑电路具有如下特点
- 电路的基本工作信号是二值信号。它表现为电路中电压的“高”或“低”、开关的“接通”或“断开”、晶体管的“导通”或“截止”等两种稳定的物理状态。
- 电路中的半导体器件一般都工作在开、关状态。
- 电路结构简单、功耗低、便于集成制造和系列化生产;产品价格低廉、使用方便、通用性好。
- 由数字逻辑电路构成的数字系统工作速度快、精度高、功能强、可靠性好。
2)数字逻辑电路类型
根据一个电路是否具有记忆功能,可将数字逻辑电路分为组合逻辑电路和时序逻辑电路两种类型。
- 组合逻辑(Combinational Logic)电路 : 在任何时刻的稳定输出仅取决于该时刻的输入而与电路过去的输入无关的逻辑电路,不需要有记忆功能。
- 时序逻辑(Sequential Logic)电路:在任何时刻的稳定输出不仅取决于该时刻的输入而且与过去的输入相关的逻辑电路,需要有记忆功能。
时序逻辑电路按照是否有统一的时钟信号进行同步,又可进一步分为同步时序逻辑电路和异步时序逻辑电路。
二、数制转换(B、Oct、D、Hex)
1. 进位计数制
一种进位计数制包含着基数和位权两个基本的因素
- 基数: 指计数制中所用到的数字符号的个数。在基数为R计数制中,包含0、1、…、R-1共R个数字符号,进位规律是“逢R进一”。称为R进位计数制,简称R进制。
- 位权: 是指在一种进位计数制表示的数中,用来表明不同数位上数值大小的一个固定常数。不同数位有不同的位权,某一个数位的数值等于这一位的数字符号乘上与该位对应的位权。R进制数的位权是R的整数次幂。
-
十进制数的位权是10的整数次幂,其个位的位权是10⁰,十位的位权是10¹……
- 一个R进制数N可以有两种表示方法
- 并列表示法(又称位置计数法)
(N)R = ( Kn-1Kn-2…K1K0 · K-1K-2…K-m )R - 多项式表示法(又称按权展开法)
(N)R = Kn-1×Rn-1 + Kn-2×Rn-2 + … + K1×R1 + K0×R0 + K-1×R-1 + K-2×R-2 + … + K-m×R-m = Σ i = − m n − 1 ^{n-1}_ {i=-m} i=−mn−1KiRi- R —— 基数
- n —— 整数部分的位数
- m —— 小数部分的位数
- Ki —— R进制中的一个数字符号,其取值范围为0≤Ki≤R-1(-m≤i≤n-1)
- R进制的特点可归纳如下
- 有0、1、…、R-1共R个数字符号
- “逢R进一”
- 位权是R的整数次幂,第i位的权为Ri(-m≤i≤n-1)
- 并列表示法(又称位置计数法)
1)十进制(D)
- 十进制中采用了0、1、…、9共十个基本数字符号,进位规律是“逢十进一”。
- 当用若干个数字符号并在一起表示一个数时,处在不同位置的数字符号,其值的含意不同。
-
(666)₁₀=6×10²+6×10¹+6×10⁰
同一个字符6从左到右所代表的值依次为600、60、6。
2)二进制(B)
- 基数R=2的进位计数制称为二进制。二进制数中只有0和1两个基本数字符号,进位规律是“逢二进一”。二进制数的位权是2的整数次幂。
- 任意一个二进制数N可以表示成
(N)2 = (Kn-1Kn-2…K1K0·K-1K-2…K-m)2 = Kn-1×2n-1 + Kn-2×2n-2 + … + K1×21 + K0×20 + K-1×2-1 + K-2×2-2 + … + K-m × 2-m = Σ i = − m n − 1 ^{n-1}_ {i=-m} i=−mn−1Ki2i- n —— 整数位数
- m —— 小数位数
- Ki —— 0或者1,-m ≤ i ≤ n-1
-
一个二进制数1011.01可以表示成:
(1011.01)2 = 1×23+0×22+1×21+1×20+0×2-1+1×2-2 - 二进制数运算规则
| 加法规则 | 减法规则 | 乘法规则 | 除法规则 |
| 0+0=0 | 0-0=0 | 0×0=0 | 0÷1=0 |
| 0+1=1 | 1-0=1 | 0×1=0 | |
| 1+0=1 | 1-1=0 | 1×0=0 | 1÷1=1 |
| 1+1=0 (进位为1) | 0-1=1 (借位为1) | 1×1=1 |
3)八进制(Oct)
- 基数R=8的进位计数制称为八进制。八进制数中有0、1、…、7共8个基本数字符号,进位规律是“逢八进一”。八进制数的位权是8的整数次幂。
- 任意一个八进制数N可以表示成
(N)8 = (Kn-1Kn-2…K1K0·K-1K-2…K-m)8 = Kn-1×8n-1 + Kn-2×8n-2 + … + K1×81+K0×80 + K-1×8-1 + K-2×8-2 + … + K-m×8-m = Σ i = − m n − 1 ^{n-1}_{i=-m} i=−mn−1Ki8i- n —— 整数位数
- m —— 小数位数
- Ki —— 0~7中的任何一个字符,-m ≤ i ≤ n-1
4)十六进制(Hex)
- 基数R=16的进位计数制称为十六进制。十六进制数中有0、1、…、9、A、B、C、D、E、F共16个数字符号,其中,A~F分别表示十进制数的10~15。进位规律为“逢十六进一”。十六进制数的位权是16的整数次幂。
- 任意一个十六进制数N可以表示成
(N)16 = (Kn-1Kn-2…K1K0·K-1K-2…K-m)16 = Kn-1×16n-1 + Kn-2×16n-2 + … + K1×161+K0×160 + K-1×16-1+K-2×16-2+…+K-m×16-m = Σ i = − m n − 1 ^{n-1}_{i=-m} i=−mn−1Ki16i- n —— 整数位数
- m —— 小数位数
- Ki —— 0~9、A~F中的任何一个字符,-m ≤ i ≤ n-1
2. 数值转换
1)二进制数与十进制数之间的转换
①二进制数转换为十进制数(多项式替代法)
将二进制数表示成按权展开式,并按十进制运算法则进行计算
(10110.101)2 = 1×24+0×23+1×22+1×21+0×20+1×2-1+0×2-2+1×2-3 = 16+4+2+0.5+0.125 = (22.625)10
②十进制数转换为二进制数(基数乘除法)
对整数和小数分别进行处理。
- 整数转换——采用“除2取余”的方法
将十进制整数N除以2,取余数计为K0;再将所得商除以2,取余数记为K1……依此类推,直至商为0,取余数计为Kn-1为止。即可得到与N对应的n位二进制整数Kn-1…K1K0。 -
(35)10 = (100011)2

- 小数转换——采用“乘2取整”的方法
将十进制小数N乘以2,取积的整数记为K–1;再将积的小数乘以2,取整数记为K–2……依此类推,直至其小数为0或达到规定精度要求,取整数记作K–m为止。即可得到与N对应的m位二进制小数0.K-1K-2…K-m。 -
(0.6875)10=(0.1011)2

2)二进制数与八进制数之间的转换
①二进制数转换为八进制数
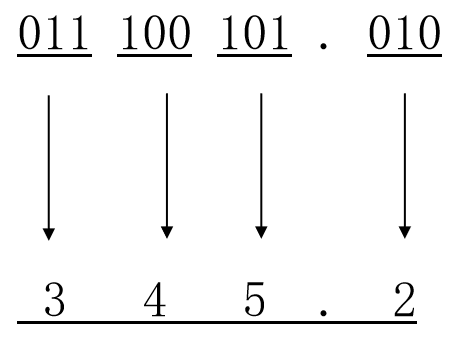
以小数点为界,分别往高、往低每3位为一组,最后不足3位时用0补充,然后写出每组对应的八进制字符,即为相应八进制数。
(11100101.01)2 = (345.2)8
②八进制数转换成二进制数
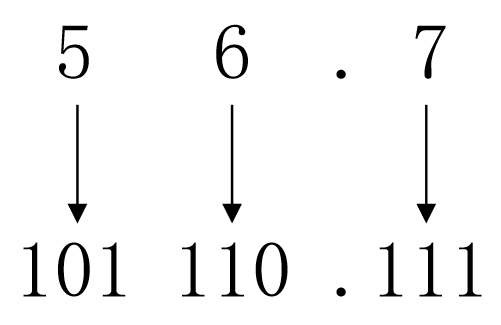
将每位八进制数用3位二进制数表示,小数点位置保持不变。
(56.7)8 = (101110.111)2
3)二进制数与十六进制数之间的转换
①二进制数转换成十六进制数
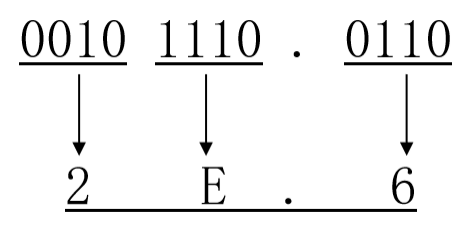
以小数点为界,分别往高、往低每4位为一组,最后不足4位时用0补充,然后写出每组对应的十六进制字符。
(101110.011)2 = (2E.6)16
②十六进制数转换成二进制数
将每位十六进制数用4位二进制数表示,小数点位置保持不变。
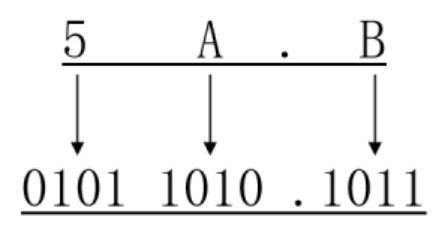
(5A.B)16 = (1011010.1011)2
三、三码1——机器码(补码余码反码)
在数字系统中,符号和数值一样是用0和1来表示的,一般将数的最高位作为符号位,用0表示正,用1表示负。
- 格式为
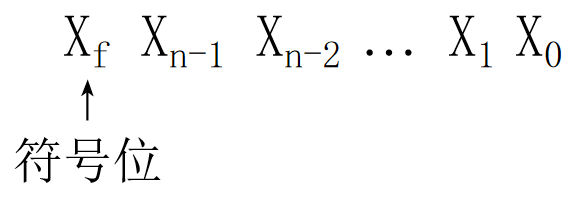
- 通常将用“+”、“-”表示正、负的二进制数称为符号数的真值,而把将符号和数值一起编码表示的二进制数称为机器数或机器码。
1. 原码
- 符号位——用0表示正,1表示负。
数值位——保持不变。 - 原码表示法又称为符号——数值表示法。
1)小数原码的定义
设二进制小数X = ± 0.x-1x-2…x-m
| [X]原 | X | 0 ≤ X < 1 |
| 1-X | -1 < X ≤ 0 |
| 符号位 | 0 | 正 |
| 1 | 负 | |
| 数值位 | 不变 | |
若 X1 = +0.1011,X2 = -0.1011
则 [X1]原 = 0.1011,[X2]原 = 1-(-0.1011) = 1.1011
小数“0”的原码可以表示成0.0…0或1.0…0。
2)整数原码的定义
设二进制整数 X = ± xn-1xn-2…x0
| [X]原 | X | 0 ≤ X < 2ⁿ |
| 2ⁿ-X | -2ⁿ < X ≤ 0 |
若X1 = +1101,X2 = -1101
[X1]原 = 01101,[X2]原 = 24-(-1101) = 10000+1101 = 11101
整数“0”的原码可以表示成00…0和10…0。
2. 反码
- 符号位——用0表示正,用1表示负。
数值位——正数反码的数值位和真值的数值位相同;而负数反码的数值位是真值的数值位按位变反。
1)小数反码的定义
设二进制小数 X = ± 0.x-1x-2…x-m
| [X]反 | X | 0 ≤ X < 1 |
| (2-2⁻ᵐ)+X | -1 < X ≤ 0 |
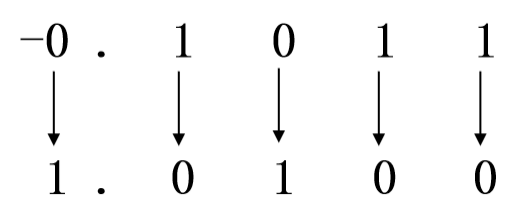
若X1 = +0.1011,X2 = -0.1011
[X1]反 = 0.1011,[X2]反 = 2-2-4+X2 = 10.0000-0.0001-0.1011=1.0100
小数“0”的反码可以表示成.0…0和1.1…1。
2)整数反码的定义
设二进制整数 X = ± xn-1xn-2…x0
| [X]反 | X | 0 ≤ X < 2ⁿ |
| (2ⁿ⁺¹-1)+X | -2ⁿ < X ≤ 0 |
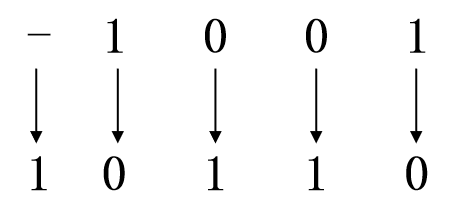
若X1 = +1001,X2 = -1001
[X1]反 = 01001,[X2]反 = (25-1)+X = (100000-1)+(-1001) = 11111-1001 = 10110
整数“0”的原码可以表示成00…0和10…0。
3)反码加减法
- [X1+X2]反 =[X1]反+[X2]反
- [X1-X2]反 = [X1]反+[-X2]反
运算时,符号位和数值位一样参加运算。当符号位有进位产生时,应将进位加到运算结果的最低位,才能得到最后结果。
3. 补码
- 符号位——用0表示正,用1表示负。
- 数值位——正数补码的数值位与真值相同;负数补码的数值位是真值的数值位按位变反,并在最低位加1。
1)小数补码的定义
设二进制小数 X = ± 0.x-1x-2…x-m
| [X]补 | X | 0 ≤ X < 1 |
| 2+X | -1 < X ≤ 0 |
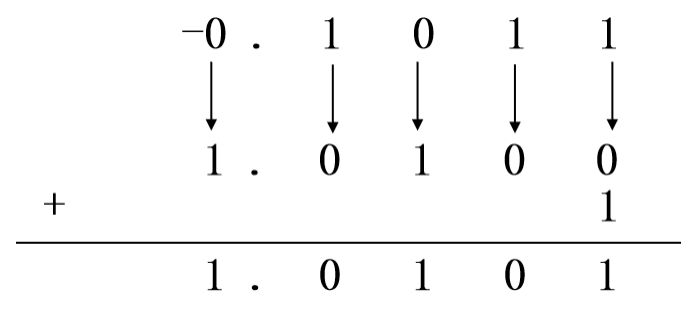
X1 = +0.1011,X2 = -0.1011
[X1]补 = 0.1011,[X2]补 = 2+X = 10.0000-0.1011 = 1.0101
小数“0”的补码只有一种表示形式,即0.0…0。
2)整数补码的定义
设二进制整数 X = ± xn-1xn-2…x0
| [X]补 | X | 0 ≤ X < 2ⁿ |
| 2ⁿ⁺¹+X | -2ⁿ < X ≤ 0 |
X1 = +1010,X2 = -1010
[X1]补= 01010(正数补码的数值位与真值相同)
[X2]补= 25 + X = 100000-1010 = 10110(负数补码的数值位是真值的数值位按位变反,并在最低位加1)
整数“0”的补码只有一种表示形式,即00…0。
3)补码加减法
- [X1+X2]补 =[X1]补+[X2]补
- [X1–X2]补 =[X1]补+[-X2]补
运算时,符号位和数值位一样参加运算,若符号位有进位产生,则应将进位丢掉后才能得到正确结果。
四、三码2——BCD码(8421、2421、余3)
- 用4位二进制代码对十进制数字符号进行编码,简称为二-十进制代码,或称BCD(Binary Coded Decimal)码。
- BCD码既有二进制的形式,又有十进制的特点。
- 常用的3种BCD码
| 十进制 | 8421 | 2421 | 余3 |
|---|---|---|---|
| 0 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0100 |
| 2 | 0010 | 0010 | 0101 |
| 3 | 0011 | 0011 | 0110 |
| 4 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1000 |
| 6 | 0110 | 1100 | 1001 |
| 7 | 0111 | 1101 | 1010 |
| 8 | 1000 | 1110 | 1011 |
| 9 | 1001 | 1111 | 1100 |
1. 8421码
- 8421码:用4位二进制码表示一位十进制字符的一种有权码,4位二进制码从高位至低位的权依次为23、22、21、20,即为8、4、2、1,故称为8421码。
- 按8421码编码的0~9与用4位二进制数表示的0~9完全一样。
8421码是一种人机联系时广泛使用的中间形式。
1)8421码与十进制数之间的转换
8421码与十进制数之间的转换是按位进行的,即十进制数的每一位与4位二进制编码对应。
(258)10 = (0010 0101 1000)8421码
(0001 0010 0000 1000)8421码 = (1208)10
2)8421码与二进制的区别
(28)10 =(11100)2 =(00101000)8421
注*
- 8421码中不允许出现1010~1111六种组合(因为没有十进制数字符号与其对应,为10~15)。
- 十进制数字符号的8421码与相应ASCII码的低四位相同,这一特点有利于简化输入输出过程中BCD码与字符代码的转换。
2. 2421码
- 是用4位二进制码表示一位十进制字符的另一种有权码,4位二进制码从高位至低位的权依次为2、4、2、1,故称为2421码。
- 若一个十进制字符X的2421码为a3、a2、a1、a0,则该字符的值为 X = 2a3 + 4a2 + 2a1 + 1a0
-
(1101)2421码 = (7)10
1)2421码与十进制数之间的转换
2421码与十进制数之间的转换是按位进行的。
(258)10 = (0010 1011 1110)2421码
(0010 0001 1110 1011)2421码 = (2185)10
注*
- 2421码不具备单值性。例如,0101和1011都对应十进制数字5。为了与十进制字符一一对应,2421码不允许出现0101~1010的6种状态。
- 2421码是一种对9的自补代码。即一个数的2421码只要自身按位变反,便可得到该数对9的补数的2421码。具有这一特征的BCD码可给运算带来方便,因为直接对BCD码进行运算时,可利用其对9的补数将减法运算转化为加法运算。
-
(4)10 → (0100)2421 → (1011)2421 → (5)10
3. 余3码
由8421码加上0011形成的一种无权码,由于它的每个字符编码比相应8421码多3,故称为余3码。
十进制字符5的余3码等于5的8421码0101加上0011,即为1000。
注*
- 余3码中不允许出现0000、0001、0010、1101、1110和1111六种状态。
- 余3码是一种对9的自补代码。
-
(256)10 = (0101 1000 1001)余3码
- 余3码与十进制数进行转换时,每位十进制数字的编码都应余3。
(1000 1001 1001 1011)余3码 = (5668)10
最后
以上就是要减肥吐司最近收集整理的关于数字逻辑 | 期末复习 · 基本知识第一章 基本知识的全部内容,更多相关数字逻辑内容请搜索靠谱客的其他文章。








发表评论 取消回复