多智能体系统——具有非线性不确定干扰的多智能体系统的固定时间事件触发一致性控制（附论文链接+源码Matlab）

多智能体系统——具有非线性不确定干扰的多智能体系统的固定时间事件触发一致性控制

Liu J, Yu Y, Wang Q, et al. Fixed-time event-triggered consensus control for multi-agent systems with nonlinear uncertainties[J]. Neurocomputing, 2017, 260: 497-504.

研究内容：
  研究具有非线性不确定性的多智能体系统的固定时间事件触发一致性控制问题。固定时间一致性协议是基于事件触发策略提出的，可以显著降低能耗和控制器更新频率。同时考虑了集中式和分布式的一致性控制策略。证明了所提出的事件触发一致性控制策略避免了芝诺行为。与有限时间一致性相比，固定时间一致性可以在沉淀时间内实现，沉淀时间与系统的初始状态无关。并给出了两个实例来说明固定时间事件触发一致性协议的有效性。

系统模型：

${\dot{x}}_i(t)=u_i(t)+f\left(x_i(t),t\right)$

控制协议：

$\begin{array}{rl}{u}_i(t)=& -c_4{\left(\sum _{j=1}^M{a}_{ij}\left(x_i\left(t_c^i\right)-x_j\left(t_c^i\right)\right)\right)}^{\alpha }\\ & -c_5{\left(\sum _{j=1}^M{a}_{ij}\left(x_i\left(t_c^i\right)-x_j\left(t_c^i\right)\right)\right)}^{\beta }\\ & -c_6\left(\sum _{j=1}^M{a}_{ij}\left(x_i\left(t_c^i\right)-x_j\left(t_c^i\right)\right)\right)\end{array}$

测量误差：

${\zeta }_i(t)=c_4{\epsilon }_i^{\alpha }(t)+c_5{\epsilon }_i^{\beta }(t)+c_6{\epsilon }_i(t)-c_4{y}_i^{\alpha }(t)-c_5{y}_i^{\beta }(t)-c_6{y}_i(t)$

$y_i(t)={\sum }_{j=1}^M{a}_{ij}(x_i(t)-x_j(t))$
${\epsilon }_i(t)={\sum }_{j=1}^M{a}_{ij}(x_i(t_c^i)-x_j(t_c^i))$

触发函数：

$|{\zeta }_i(t)|\le \frac{1}{2}{c}_6|y_i(t)|$

当$|{\zeta }_i(t)|>\frac{1}{2}{c}_6|y_i(t)|$事件触发，在任何事件触发时刻，智能体$i$将更新控制法，测量误差将被设置为零。

定理：

当系统参数满足$2\gamma \le c_6{\lambda }_2$，多智能体系统可实现固定时间事件触发一致性，沉淀时间$T$:$$T\le T_{\max }:=\frac{1}{c_4{2}^{\frac{\alpha -1}{2}}{\lambda }_2^{\frac{\alpha +1}{2}}(1-\alpha )}+\frac{1}{c_5{2}^{\frac{\beta -1}{2}}{\lambda }_2^{\frac{\beta +1}{2}}{M}^{\frac{1-\beta }{2}}(\beta -1)}$$

//仿真案例

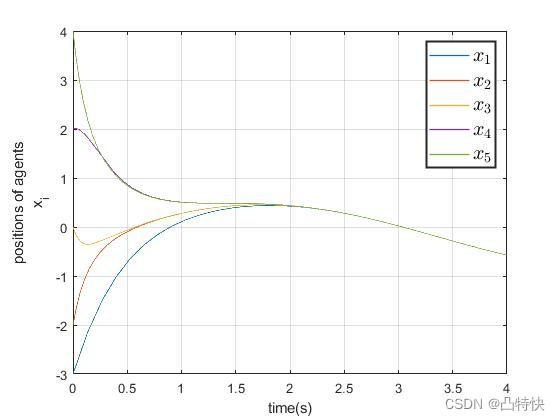
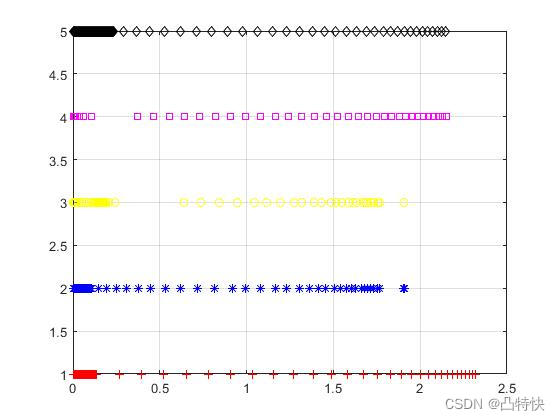
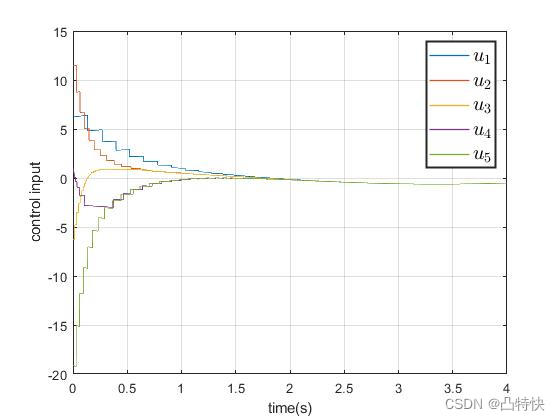
链接????：Matlab

MATLAB源程序：请私信获取，请及时关注回复。

https://zhuanlan.zhihu.com/p/452608935

最后

以上就是忧虑母鸡为你收集整理的多智能体系统——具有非线性不确定干扰的多智能体系统的固定时间事件触发一致性控制（附论文链接+源码Matlab）的全部内容，希望文章能够帮你解决多智能体系统——具有非线性不确定干扰的多智能体系统的固定时间事件触发一致性控制（附论文链接+源码Matlab）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。