概述
ID3 算法是构建决策树算法中一种非常重要的算法,可以说它是学习决策树算法的基础吧。ID3又叫做迭代二分器,是以信息增益为准则选择划分属性的,对可取值数目较多的属性有所偏好。本文整合了两位大神的博客,介绍了一些基本原理和西瓜书的随对应的决策树习题4.3,再次感谢。
引言
如果你是刚刚才接触到有关决策树的相关内容,那么你可能就会有一些疑问,什么是决策树?对于什么是决策树这个话题,如果站在编程的角度来类比,我想 if … else 是最贴切的了吧。就比如下面的这样的一棵最简单的决策树。 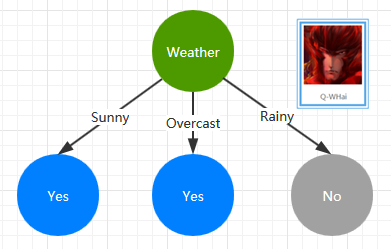
这是一棵是否出门打球的决策树,而决策的特征属性就是 Weather,如果天气状态为 Sunny、Overcast 则选择出门打球;如果下雨了那就只能待在家里了。
如果上面的这棵决策树是按照我的选择来构建的,那么你的选择又会构建成一棵什么样的决策树呢?也就是说某一棵决策树只能代表某一种情况,可是我们是想拿构建好的决策树进行预测的,所以这时,就不能再只按照某一个人的意愿来构建决策树了。我们需要收集大量的训练数据,并使用这些训练数据进行构建决策树。
基础知识
数据挖掘的基础是数学,如果数学不太好,就一定要好好补补了(我也是数学不太好的那些人当中的一个)。ID3 算法当然也不例外地涉及了一些数学知识。主要的是两块内容:信息熵与信息增益。
信息熵
信息熵简介
中学时期,我们都有学习过熵的概念,主要是在物理跟化学中。在物理学科中,熵是用来描述分子的混乱程度的,在化学学科中也是类似的,如果我没有记错的话,当时熵在化学中的应用主要是某一化合物的加热这一块,比如给水加热,会变化水蒸汽,这时熵就是增大的;还就是化合反应这一块。
那么在本文的 ID3 算法中,或者说在数据挖掘中的信息熵要怎么理解或是怎么应用呢?这里不妨打个最简单的比方,我们说假设有两篇文章,分别为:Article_1 和 Article_2,它们的内容如下:
Article_1
<code class="hljs has-numbering" style="display: block; padding: 0px; color: inherit; box-sizing: border-box; font-family: 'Source Code Pro', monospace;font-size:undefined; white-space: pre; border-radius: 0px; word-wrap: normal; background: transparent;">信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵
信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵
信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵
信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵信息熵</code><ul class="pre-numbering" style="box-sizing: border-box; position: absolute; width: 50px; top: 0px; left: 0px; margin: 0px; padding: 6px 0px 40px; border-right-width: 1px; border-right-style: solid; border-right-color: rgb(221, 221, 221); list-style: none; text-align: right; background-color: rgb(238, 238, 238);"><li style="box-sizing: border-box; padding: 0px 5px;">1</li><li style="box-sizing: border-box; padding: 0px 5px;">2</li><li style="box-sizing: border-box; padding: 0px 5px;">3</li><li style="box-sizing: border-box; padding: 0px 5px;">4</li></ul><ul class="pre-numbering" style="box-sizing: border-box; position: absolute; width: 50px; top: 0px; left: 0px; margin: 0px; padding: 6px 0px 40px; border-right-width: 1px; border-right-style: solid; border-right-color: rgb(221, 221, 221); list-style: none; text-align: right; background-color: rgb(238, 238, 238);"><li style="box-sizing: border-box; padding: 0px 5px;">1</li><li style="box-sizing: border-box; padding: 0px 5px;">2</li><li style="box-sizing: border-box; padding: 0px 5px;">3</li><li style="box-sizing: border-box; padding: 0px 5px;">4</li></ul>Article_2
<code class="hljs mathematica has-numbering" style="display: block; padding: 0px; color: inherit; box-sizing: border-box; font-family: 'Source Code Pro', monospace;font-size:undefined; white-space: pre; border-radius: 0px; word-wrap: normal; background: transparent;">信息论之父 <span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">C</span>. <span class="hljs-keyword" style="color: rgb(0, 0, 136); box-sizing: border-box;">E</span>. Shannon 在 <span class="hljs-number" style="color: rgb(0, 102, 102); box-sizing: border-box;">1948</span> 年发表的论文“通信的数学理论( A Mathematical Theory of Communication )”中, Shannon 指出,任何信息都存在冗余,冗余大小与信息中每个符号(数字、字母或单词)的出现概率或者说不确定性有关。
Shannon 借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式。</code><ul class="pre-numbering" style="box-sizing: border-box; position: absolute; width: 50px; top: 0px; left: 0px; margin: 0px; padding: 6px 0px 40px; border-right-width: 1px; border-right-style: solid; border-right-color: rgb(221, 221, 221); list-style: none; text-align: right; background-color: rgb(238, 238, 238);"><li style="box-sizing: border-box; padding: 0px 5px;">1</li><li style="box-sizing: border-box; padding: 0px 5px;">2</li></ul><ul class="pre-numbering" style="box-sizing: border-box; position: absolute; width: 50px; top: 0px; left: 0px; margin: 0px; padding: 6px 0px 40px; border-right-width: 1px; border-right-style: solid; border-right-color: rgb(221, 221, 221); list-style: none; text-align: right; background-color: rgb(238, 238, 238);"><li style="box-sizing: border-box; padding: 0px 5px;">1</li><li style="box-sizing: border-box; padding: 0px 5px;">2</li></ul>对于上面的这两篇文章,我们要怎么衡量其信息量呢?文章的字数么?显然不是的,第一篇文章的字数要比第二篇文章的字数要多,然而其包含的信息量却要小一些。于是,信息熵的概念就此被引出,结合上面对熵的描述,你也可以理解成信息熵就是信息的混乱程度。
信息熵公式
假如一个随机变量 X 的取值为 X = {x1,x1,...,xn},每一种取到的概率分别是 {p1,p1,...,pn},那么 X 的熵定义为
H(x)=−∑i=1npilog2pi
信息增益
信息增益简介
信息增益的功能是描述一个特征属性对于总体的重要性,怎么理解这句话呢?打个比方吧,比如我想出去打球,这里可能会受到天气、温度、心情等等的因素地影响。那么对于天气这个特征属性而言,有天气这个属性跟没有天气这个属性,总体的信息量(也就是信息熵)的变化就是信息增益了。
可能这里还不太清楚信息增益在决策树的构建中产生了什么作用,这个问题我们留到 ID3 算法部分再详细说明。
信息增益公式
IG(S|T)=Entropy(S)−∑value(T)|Sv|SEntropy(Sv)
其中 S 为全部样本集合,value(T) 是属性 T 所有取值的集合,v 是 T 的其中一个属性值,Sv是 S 中属性 T 的值为 v 的样例集合,|Sv| 为 Sv 中所含样例数。
ID3
决策树构建分析
ID3 是数据挖掘中的一种非常重要的决策树构建算法,它是一种监督学习式的机器学习。由于这是一种监督学习,所以必然需要有一定数量的训练数据集,而每一条训练数据所形成的决策树都不一定是完全一样的。打个比方,假设有如下三条训练数据:
| Day | OutLook | Temperature | Humidity | Wind | PlayTennis |
|---|---|---|---|---|---|
| 1 | Sunny | Hot | High | Weak | No |
| 2 | Sunny | Hot | High | Strong | No |
| 3 | Rainy | Mild | High | Weak | Yes |
那么对于 OutLook 这一特征属性而言,就有两种不同的状态值:Sunny 和 Rainy。就算是对于同一个 OutLook 状态值时,其结果分类也是一样的,这样我们构建的决策的标准是什么呢?
训练数据集
假设我们如下训练数据集
| Day | OutLook | Temperature | Humidity | Wind | PlayTennis |
|---|---|---|---|---|---|
| 1 | Sunny | Hot | High | Weak | No |
| 2 | Sunny | Hot | High | Strong | No |
| 3 | Overcast | Hot | High | Weak | Yes |
| 4 | Rainy | Mild | High | Weak | Yes |
| 5 | Rainy | Cool | Normal | Weak | Yes |
| 6 | Rainy | Cool | Normal | Strong | No |
| 7 | Overcast | Cool | Normal | Strong | Yes |
| 8 | Sunny | Mild | High | Weak | No |
| 9 | Sunny | Cool | Normal | Weak | Yes |
| 10 | Rainy | Mild | Normal | Weak | Yes |
| 11 | Sunny | Mild | Normal | Strong | Yes |
| 12 | Overcast | Mild | High | Strong | Yes |
| 13 | Overcast | Hot | Normal | Weak | Yes |
| 14 | Rainy | Mild | High | Strong | No |
决策树构建过程
下面是我根据 ID3 构建决策树的算法步骤,绘制的决策树构建过程图。因为 ID3 其实是一个迭代的算法,这里我只绘制了一次迭代的过程,所以是一个局部示图。 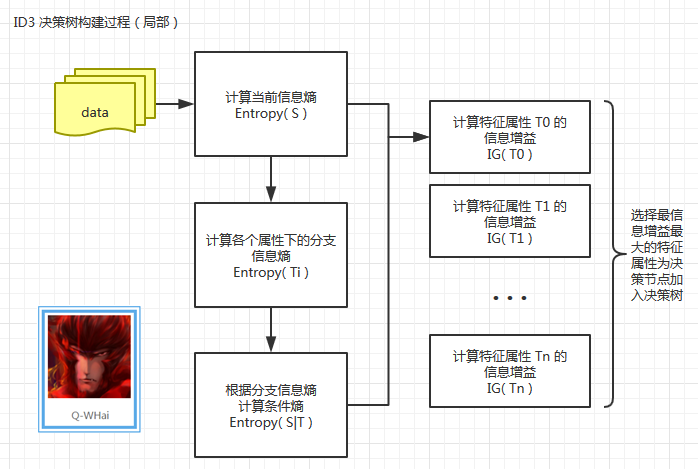
当上面的局部过程中的最后一步计算出了最大信息增益之后,我们要将这个最大信息增益对应的特征属性进行移除,并将数据集切分成 N 个部分(其中 N 为分支状态数)。
现在假设我们计算出当选择特征属性为 OutLook 的时候,其信息增益最大,那么原始数据就会被切分成如下 3 份:
part_sunny
| Day | Temperature | Humidity | Wind | PlayTennis |
|---|---|---|---|---|
| 1 | Hot | High | Weak | No |
| 2 | Hot | High | Strong | No |
| 3 | Mild | High | Weak | No |
| 4 | Cool | Normal | Weak | Yes |
| 5 | Mild | Normal | Strong | Yes |
part_overcast
| Day | Temperature | Humidity | Wind | PlayTennis |
|---|---|---|---|---|
| 1 | Hot | High | Weak | Yes |
| 2 | Cool | Normal | Strong | Yes |
| 3 | Mild | High | Strong | Yes |
| 4 | Hot | Normal | Weak | Yes |
part_rainy
| Day | Temperature | Humidity | Wind | PlayTennis |
|---|---|---|---|---|
| 1 | Mild | High | Weak | Yes |
| 2 | Cool | Normal | Weak | Yes |
| 3 | Cool | Normal | Strong | No |
| 4 | Mild | Normal | Weak | Yes |
| 5 | Mild | High | Strong | No |
这样再把这 3 份数据分别当成上图中的 data 代入计算。通过这样循环地迭代,直到数据被全部计算完成。
计算步骤
如果上面信息熵跟信息增益的计算公式,让你看得有一些不是很懂,没关系。这里我会通过几个示例来分析一下计算过程,这样你就会更懂一些了。
1. Entropy(S)
2. Entropy(Ti)
3. Entropy(S|T)
4. IG(T)
Entropy(S)
对于最初始的 14 条记录,我们统计了结果分类,其中,Yes = 9,No = 5.
这时当前信息的信息熵计算过程如下:
Entropy(S)=−914log2914−514log2514=0.940286
Entropy(Ti)
假设这时我们需要计算最初始的 14 条记录中,特征属性为 OutLook 的分支状态信息熵。首先需要做的是,统计 OutLook 特征属性下的结果分类分布。
| Sunny | Overcast | Rainy | |
|---|---|---|---|
| Yes | 2 | 4 | 3 |
| No | 3 | 0 | 2 |
各个特征属性下的分支状态信息熵计算过程如下:
Entropy(Sunny)=−25log225−35log235=0.970951
Entropy(Overcast)=−44log244−04log204=0
Entropy(Rainy)=−35log235−25log225=0.970951
Entropy(S|T)
统计完各个分支状态的信息熵之后,就需求合并,也就是某一特征属性的信息熵了。
Entropy(S|OutLook)=514∗Entropy(Sunny)+414∗Entropy(Overcast)+514∗Entropy(Rainy)=0.693536
IG(T)
我们还是拿上面的数据进行计算。也就是计算 IG(OutLook).
IG(OutLook)=Entropy(S)−Entropy(S|OutLook)=0.940286−0.693536=0.24675
决策树构建结果
通过上面的训练数据集及 ID3 构建算法,我们构建了一棵如下的 ID3 决策树。 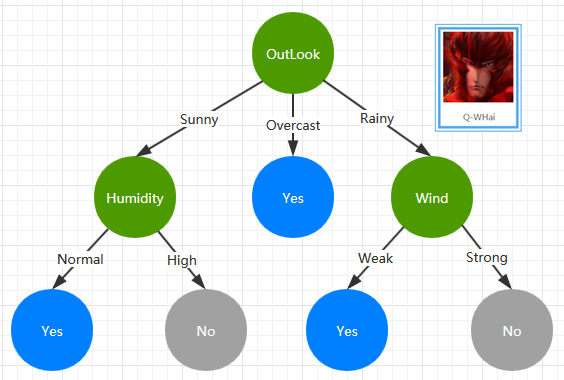
周志华《机器学习》第四章习题4.3
编程实现基于信息熵进行划分选择的决策树算法,为书中表4.3生成一棵决策树。
表4.3数据如下:
编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好坏
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,好瓜
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.744,0.376,好瓜
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,好瓜
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,好瓜
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,好瓜
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,好瓜
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,好瓜
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,好瓜
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,坏瓜
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,坏瓜
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,坏瓜
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,坏瓜
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,坏瓜
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,坏瓜
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,坏瓜
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,坏瓜
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,坏瓜
决策树输出树的数组结构,节点按树的先根遍历排序,每个节点4个属性值,依次为
1.父节点的index,规定根节点该位置的index指向自己
2.如果节点是叶节点,记录分类;如果是非叶节点,记录当前位置最佳的划分属性标签
3.记录所有的非根节点连接父节点的具体属性值,没有则为空
4.如果该属性是连续属性,则记录阈值,没有则为空。
决策树输出示例:
[[0, '纹理', [], []],
[0, '密度', '清晰', []],
[1, '坏瓜', '小于', 0.3815],
[1, '好瓜', '大于', 0.3815],
[0, '触感', '稍糊', []],
[4, '坏瓜', '硬滑', []],
[4, '好瓜', '软粘', []],
[0, '坏瓜', '模糊', []]]Python代码实现:
# -*- coding: utf-8 -*-
"""
Created on Mon Jan 16 12:01:08 2017
@author: icefire
"""
from dtreeplot import dtreeplot
import math
#属性类
class property:
def __init__(self,idnum,attribute):
self.is_continuity=False #连续型属性标记
self.attribute=attribute #属性标签
self.subattributes=[] #属性子标签
self.id=idnum #属性排在输入文本的第几位
self.index={} #属性子标签的索引值
#决策树生成类
class dtree():
'''
构造函数
filename:输入文件名
haveID:输入是否带序号
property_set:为空则计算全部属性,否则记录set中的属性
'''
def __init__(self,filename,haveID,property_set):
self.data=[]
self.data_property=[]
#读入数据
self.__dataread(filename,haveID)
#判断选择的属性集合
if len(property_set)>0:
tmp_data_property=[]
for i in property_set:
tmp_data_property.append(self.data_property[i])
tmp_data_property.append(self.data_property[-1])
else:
tmp_data_property=self.data_property
#决策树树形数组结构
self.treelink=[]
#决策树主递归
self.__TreeGenerate(range(0,len(self.data[-1])),tmp_data_property,0,[],[])
#决策树绘制
dtreeplot(self.treelink,6,1,-6)
'''
决策树主递归
data_set:当前样本集合
property_set:当前熟悉集合
father:父节点索引值
attribute:父节点连接当前节点的子属性值
threshold:如果是连续参数就是阈值,否则为空
'''
def __TreeGenerate(self,data_set,property_set,father,attribute,threshold):
#新增一个节点
self.treelink.append([])
#新节点的位置
curnode=len(self.treelink)-1
#记录新节点的父亲节点
self.treelink[curnode].append(father)
#结束条件1:所有样本同一分类
current_data_class=self.__count(data_set,property_set[-1])
if(len(current_data_class)==1):
self.treelink[curnode].append(self.data[-1][data_set[0]])
self.treelink[curnode].append(attribute)
self.treelink[curnode].append(threshold)
return
#结束条件2:所有样本相同属性,选择分类数多的一类作为分类
if all(len(self.__count(data_set,property_set[i]))==1 for i in range(0,len(property_set)-1)):
max_count=-1;
for dataclass in property_set[-1].subattributes:
if current_data_class[dataclass]>max_count:
max_attribute=dataclass
max_count=current_data_class[dataclass]
self.treelink[curnode].append(max_attribute)
self.treelink[curnode].append(attribute)
self.treelink[curnode].append(threshold)
return
#信息增益选择最优属性与阈值
prop,threshold = self.__entropy_paraselect(data_set,property_set)
#记录当前节点的最优属性标签与父节点连接当前节点的子属性值
self.treelink[curnode].append(prop.attribute)
self.treelink[curnode].append(attribute)
#从属性集合中移除当前属性
property_set.remove(prop)
#判断是否是连续属性
if(prop.is_continuity):
#连续属性分为2子属性,大于和小于
tmp_data_set=[[],[]]
for i in data_set:
tmp_data_set[self.data[prop.id][i]>threshold].append(i)
for i in [0,1]:
self.__TreeGenerate(tmp_data_set[i],property_set[:],curnode,prop.subattributes[i],threshold)
else:
#离散属性有多子属性
tmp_data_set=[[] for i in range(0,len(prop.subattributes))]
for i in data_set:
tmp_data_set[prop.index[self.data[prop.id][i]]].append(i)
for i in range(0,len(prop.subattributes)):
if len(tmp_data_set[i])>0:
self.__TreeGenerate(tmp_data_set[i],property_set[:],curnode,prop.subattributes[i],[])
else:
#如果某一个子属性不存没有对应的样本,则选择父节点分类更多的一项作为分类
self.treelink.append([])
max_count=-1;
tnode=len(self.treelink)-1
for dataclass in property_set[-1].subattributes:
if current_data_class[dataclass]>max_count:
max_attribute=dataclass
max_count=current_data_class[dataclass]
self.treelink[tnode].append(curnode)
self.treelink[tnode].append(max_attribute)
self.treelink[tnode].append(prop.subattributes[i])
self.treelink[tnode].append(threshold)
#为没有4个值得节点用空列表补齐4个值
for i in range(len(self.treelink[curnode]),4):
self.treelink[curnode].append([])
'''
信息增益算则最佳属性
data_set:当前样本集合
property_set:当前属性集合
'''
def __entropy_paraselect(self,data_set,property_set):
#分离散和连续型分别计算信息增益,选择最大的一个
max_ent=-10000
for i in range(0,len(property_set)-1):
prop_id=property_set[i].id
if(property_set[i].is_continuity):
tmax_ent=-10000
xlist=self.data[prop_id][:]
xlist.sort()
#连续型求出相邻大小值的平局值作为待选的最佳阈值
for j in range(0,len(xlist)-1):
xlist[j]=(xlist[j+1]+xlist[j])/2
for j in range(0,len(xlist)-1):
if(i>0 and xlist[j]==xlist[j-1]):
continue
cur_ent = 0
nums=[[0,0],[0,0]]
for k in data_set:
nums[self.data[prop_id][k]>xlist[j]][property_set[-1].index[self.data[-1][k]]]+=1
for k in [0,1]:
subattribute_sum=nums[k][0]+nums[k][1]
if(subattribute_sum > 0):
p=nums[k][0]/subattribute_sum
cur_ent +=(p*math.log(p+0.00001,2)+(1-p)*math.log(1-p+0.00001,2))*subattribute_sum/len(data_set)
if(cur_ent>tmax_ent):
tmax_ent = cur_ent
tmp_threshold = xlist[j]
if(tmax_ent > max_ent):
max_ent=tmax_ent;
bestprop = property_set[i];
best_threshold = tmp_threshold;
else:
#直接统计并计算
cur_ent=0
nums=[[0,0] for i in range(0,len(property_set[i].subattributes))]
for j in data_set:
nums[property_set[i].index[self.data[prop_id][j]]][property_set[-1].index[self.data[-1][j]]]+=1
for j in range(0,len(property_set[i].subattributes)):
subattribute_sum=nums[j][0]+nums[j][1]
if(subattribute_sum>0):
p=nums[j][0]/subattribute_sum
cur_ent += (p*math.log(p+0.00001,2)+(1-p)*math.log(1-p+0.00001,2))*subattribute_sum/len(data_set)
if(cur_ent > max_ent):
max_ent=cur_ent;
bestprop = property_set[i];
best_threshold = [];
return bestprop,best_threshold
'''
计算当前样本在某个属性下的分类情况
'''
def __count(self,data_set,prop):
out={}
rowdata=self.data[prop.id]
for i in data_set:
if rowdata[i] in out:
out[rowdata[i]]+=1
else:
out[rowdata[i]]=1;
return out
'''
输入数据处理
'''
def __dataread(self,filename,haveID):
file = open(filename, 'r')
linelen=0
first=1;
while 1:
#按行读
line = file.readline()
if not line:
break
line=line.strip('n')
rowdata = line.split(',')
#如果有编号就去掉第一列
if haveID:
del rowdata[0]
if(linelen==0):
#处理第一行,初始化属性类对象,记录属性的标签
for i in range(0,len(rowdata)):
self.data.append([])
self.data_property.append(property(i,rowdata[i]))
self.data_property[i].attribute=rowdata[i]
linelen=len(rowdata)
elif(linelen==len(rowdata)):
if(first==1):
#处理第二行,记录属性是否是连续型和子属性
for i in range(0,len(rowdata)):
if(isnumeric(rowdata[i])):
self.data_property[i].is_continuity=True
self.data[i].append(float(rowdata[i]))
self.data_property[i].subattributes.append("小于")
self.data_property[i].index["小于"]=0
self.data_property[i].subattributes.append("大于")
self.data_property[i].index["大于"]=1
else:
self.data[i].append(rowdata[i])
else:
#处理后面行,记录子属性
for i in range(0,len(rowdata)):
if(self.data_property[i].is_continuity):
self.data[i].append(float(rowdata[i]))
else:
self.data[i].append(rowdata[i])
if rowdata[i] not in self.data_property[i].subattributes:
self.data_property[i].subattributes.append(rowdata[i])
self.data_property[i].index[rowdata[i]]=len(self.data_property[i].subattributes)-1
first=0
else:
continue
'''
判断是否是数字
'''
def isnumeric(s):
return all(c in "0123456789.-" for c in s)
filename="西瓜3.data"
property_set=range(0,6)
link=dtree(filename,True,property_set)
结果图:
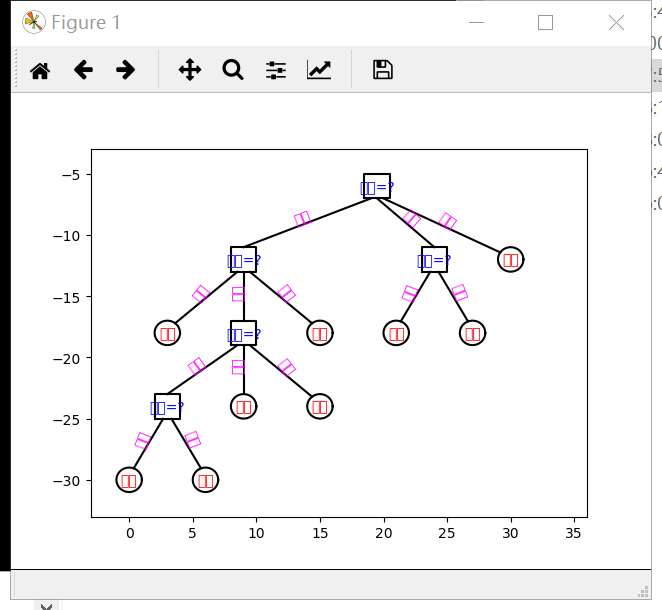
最后
以上就是爱撒娇板凳最近收集整理的关于决策树之ID3算法概述引言基础知识ID3周志华《机器学习》第四章习题4.3的全部内容,更多相关决策树之ID3算法概述引言基础知识ID3周志华《机器学习》第四章习题4内容请搜索靠谱客的其他文章。








发表评论 取消回复