决策树(一)--特征值选择

69 阅读 0 评论 46 点赞

我是靠谱客的博主义气战斗机，最近开发中收集的这篇文章主要介绍决策树(一)--特征值选择，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

决策树是一种基本的分类和回归方法。用决策树分类，从根节点开始，对实例的某一特征进行测试，根据测试的结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值，递归地对实例进行测试和分配，直至达到叶节点，最后将实例分到叶节点的类中。

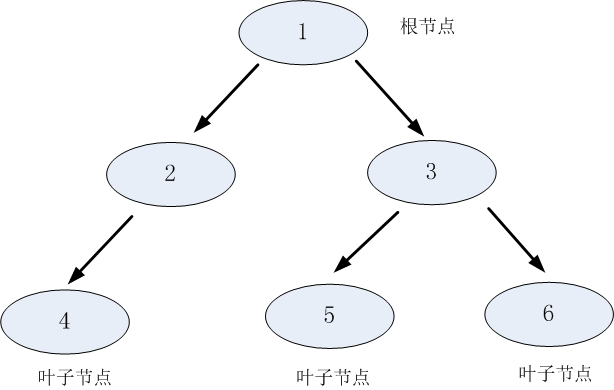
决策树学习通常包括3个步骤：特征选择，决策树的生成和决策树的剪枝。

特征值选择

当训练元组纬度比较大时，我们在对其进行分类的时候，要考虑选择哪一个特征值进行分裂得到的分类结果才是最好的。

属性选择度量是一种选择分裂准则，把给定类标记的训练元组的数据区D“最好地”划分为单独类的启发方式。这里介绍三种常用的属性选择度量-信息增益，增益率，基尼指数

1：信息增益（ID3）

为了便于说明，先给出熵和条件熵的定义

在信息论与概率统计中，熵是表示随机变量不确定性的度量，X是一个取有限个值的离散随机变量，其概率分布为 $P(X=x_{i})=p_{i}$ ，则随机变量X的熵为 $H(X)=-sum_{i=1}^{n}p_{i}log{p_{i}}$

由公式可以得知，熵只依赖于X的分布，而与X的取值无关，并且熵越大，随机变量的不确定性就越大！！！

假设有随机变量（X,Y），其联合概率分布为： $P(X=x_{i},Y=y_{i})=p_{ij}$ ，条件熵 $H(Y|X)$ 表示在已知随机变量X的条件下，Y的不确定性。随机变量X给定条件下随机变量Y的条件熵定义为X给定条件下Y的条件概率分布的熵对X的数学期望

$H(Y|X)=sum_{i=1}^{n}{p_{i}H(Y|X=x_{i})}$

信息增益定义：

特征A对训练集D的信息增益g(D,A)，定义为集合D的熵H(D)与特征A给定条件下D的条件熵H(D|A)的差，即：

$g(D,A)=H(D)-H(D|A)$ ，信息增益表示得到特征X的信息而使得类Y的信息不确定性减少的程度。

$H(D)=-sum_{k=1}^{K}{frac{|C_{k}|}{|D|}}log_{2}frac{|C_{k}|}{|D|}$

$H(D|A)=sum_{i=1}^{n}{frac{|Di|}{|D|}}sum_{k=1}^{K}{frac{|D_{ik}|}{|D_{i}|}}log_{2}frac{|D_{ik}|}{|D_{i}|}$

其中|D|表示其样本容量，K表示类的个数,|Ck|表示的属于类Ck的个数，设特征A有n个不同的取值，根据特征A的取值将D划分为n个子集Di,|Di|为Di的样本个数，记子集Di中属于类Ck的样本集合为Cik。

2：增益率（C4.5）

信息增益比：特征A对训练数集D的信息增益比 $g_{R}(D,A)$ 定义为其信息增益 $g(D,A)$ 与训练数据集D关于特征值A的值的熵 $H_{A}(D)$ 之比，即

$g_{R}(D,A)=frac{g(D,A))}{H_{A}(D)}$ ，其中 $H_{A}(D)=-sum_{i=1}^{n}{frac{|D_{i}|}{|D|}}logfrac{|D_{i}|}{|D|}$

3：基尼指数（CART）

基尼指数度量数据区或训练集D的不纯度，定义为： $Gini(D)=1-sum_{i=1}^{n}{p_{i}^2}$ ，基尼指数值越小，数据集的纯度越高。

属性A的基尼指数定义为：

$Gini(D,A)=sum_{k=1}^{K}{frac{|D_{k}|}{|D|}}Gini(D_{k})$

接下来，我们来算一下这三种度量方式

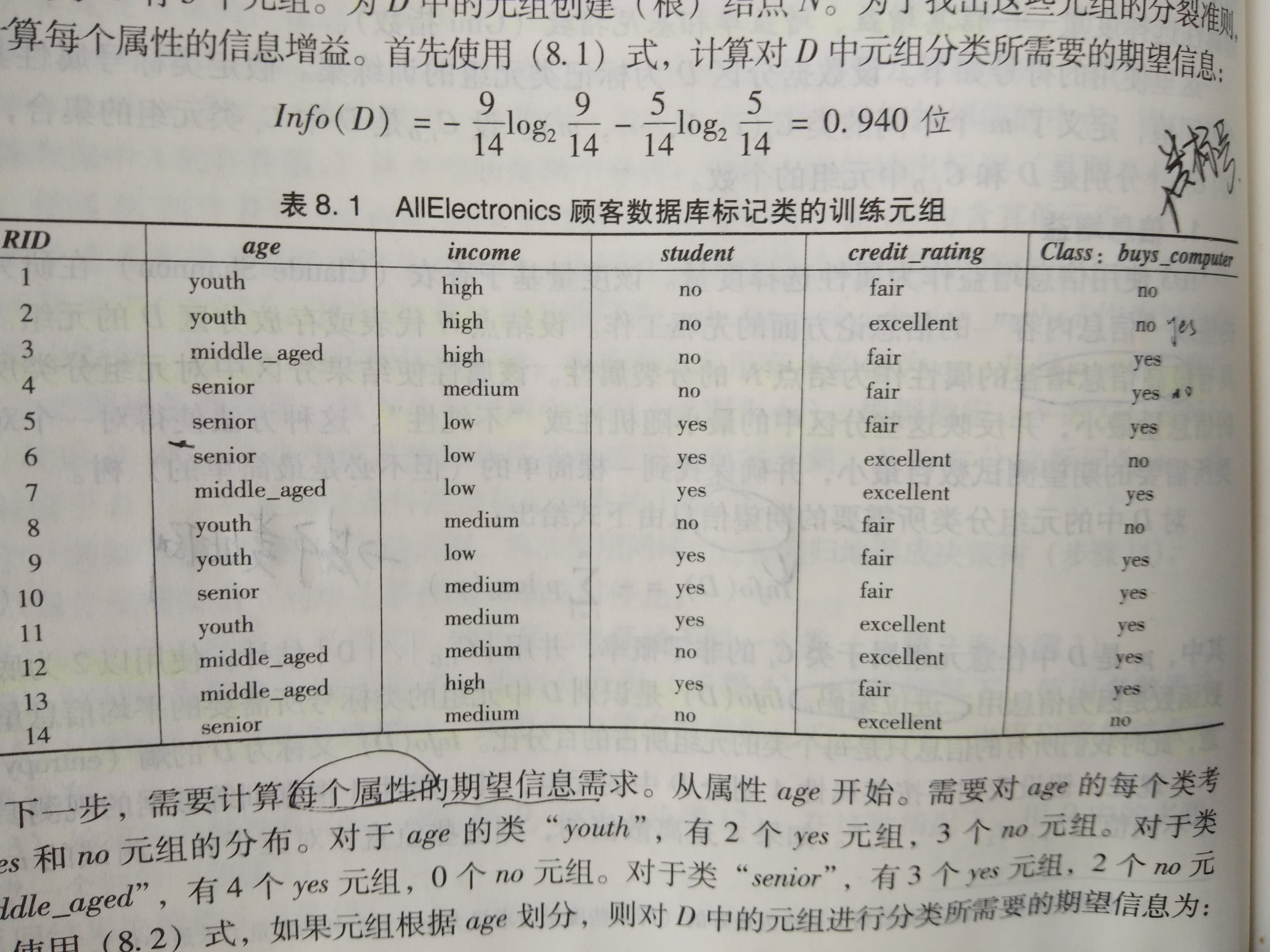
1：信息增益

标号buys_conputer有两个不同的值，因此有两个类。类yes中有9个元组，类no中有5个元组。

$Info(D)=-frac{9}{14}log_{2}frac{9}{14}-frac{5}{14}log_{2}frac{5}{14}=0.94$

下一步需要计算每个属性的期望信息需求。从age开始。需要对age中的每个类考察age和no的分布。

对于age类的"youth"，有2个yes元组和3个no元组

对于age类的"middle_aged"，有4个yes元组和0个no元组

对于age类的"senior"，有3个yes元组，2个no元组。

$Info_{age}(D)=frac{5}{14}*(-frac{2}{5}log_{2}frac{2}{5}-frac{3}{5}log_{2}frac{2}{5})+frac{4}{14}*(-frac{4}{4}log_{2}frac{4}{4}-frac{0}{4}log_{2}frac{0}{4})+frac{5}{14}*(-frac{2}{5}log_{2}frac{2}{5}-frac{3}{5}log_{2}frac{2}{5})=0.694$

因此，这种划分的信息增益为： $Gain(age)=Info(D)-Info_{age}(D)=0.940-0.694=0.246$

类似的，对于income： $Gain(income)=0.029$

对于student： $Gain(student)=0.151$

对于credit_rating： $Gain(credit_rating)=0.048$

由于age在属性中具有最高的信息增益，所以它被选做分裂属性

2：信息增益率

属性income将数据划分为3个分区，low，medium，high，分别包含4,6,4个元组。

$H{_income}(D)=-frac{4}{14}log_{2}frac{6}{14}-frac{6}{14}log_{2}frac{4}{14}-frac{4}{14}log_{2}frac{4}{14}=1.557$

$Gain(income)=0.029$ ，因此 $GainRatio(income)=0.029/1.557=0.019$

3：基尼指数

表中9个元组是属于类buy_computer=yes，而其余的5个元组属于类buy_computer=no。首先使用基尼指数计算D的不纯度

$Gain(D)=1-(frac{9}{14})^2-(frac{5}{14})^2=0.459$

针对属性income，并考虑每个可能的分裂子集，考虑子集{low,medium}，这将导致10个满足条件income在{low，medium}的元组在分区D1中，其中四个在D2中,D2为income属于{high}

$Gini_{income->high}=frac{10}{14}Gini(D1)+frac{4}{14}Gini(D2)=0.443$

类似的，用其余子集划分的基尼指数为：0.458 {low，high} 0.450 {medium，high}，因此，属性income的最好二元划分在{low，medium}上，因为他有最小的基尼指数

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	增益率	支持	支持	支持
CART	分类，回归	二叉树	基尼指数	支持	支持	支持