决策树算法

决策树

树模型

决策树：从根节点开始一步步走到叶子节点（这一过程叫做决策的过程，叶子节点就是决策）。

所有的数据最终都会落到叶子节点，既可以做分类，也可以做回归。

例如下面的图示就是一个决策的过程。

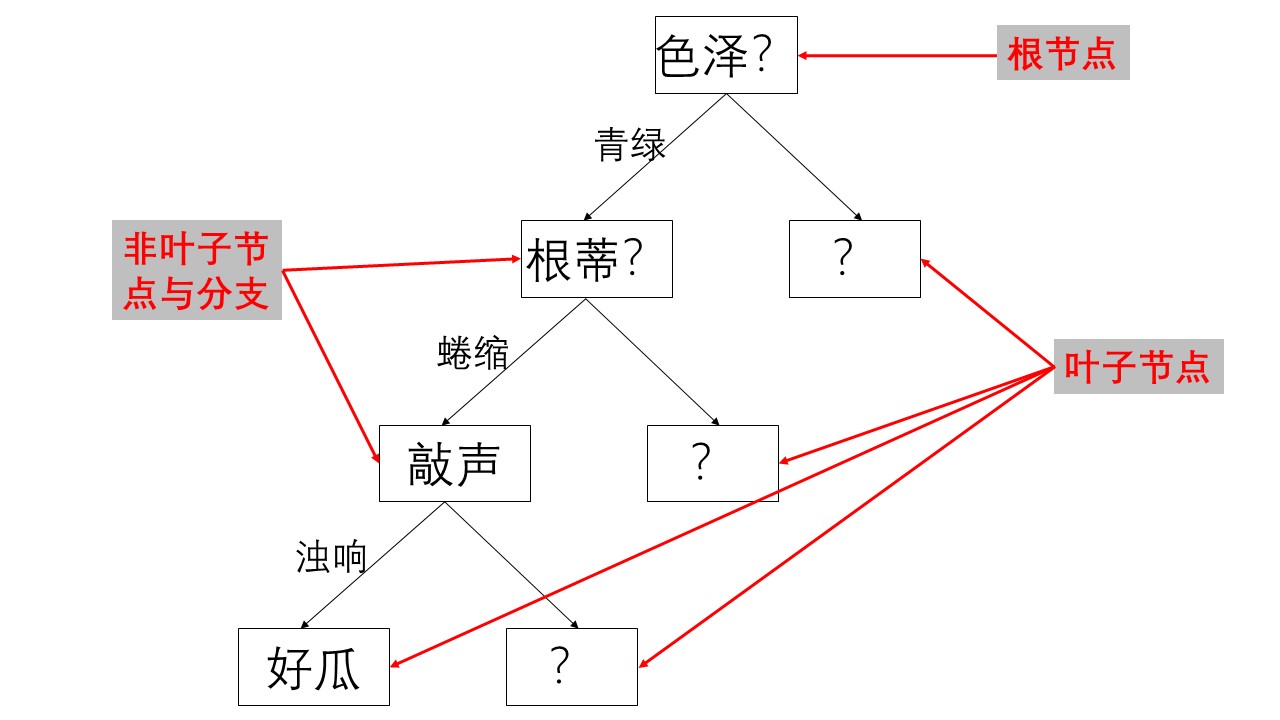
根节点：第一个选择的节点。

非叶子节点与分支：中间的决策过程

叶子节点：最终的决策结果。

节点：没增加一个节点相当于在数据中切一刀，将数据分类。

决策树的训练于测试

训练阶段：从给定的训练集构造出一棵树（从根节点开始选择特征，一步一步往下分，但是如何选择出第一个第二个…的特征呢，也就是划分特征的选择，这个分类特征的选择后面会讲到，还会涉及到树的剪枝处理，包括：预剪枝和后剪枝，以及连续数据的处理，缺失值的处理。）

测试阶段：将数据放入模型根据构造的树模型从上到下流动。

如何选择切分特征呢？也就是如何选择节点？

​ 跟节点的特征选择应该用那个特征呢？接下来的第二特征，第三特征呢？这些特征如何选择呢？在一批数据中的特征显然是多样的，但是我们不能随意地选取一个特征放到任意的一个节点上，这显然是不对的，根据排列组合原理，这样随意选择一个特征随意放到一个节点上，随后得到的模型是很多的，我们当然是要得到一个最优模型。

​ 我们的目标应该是没一个节点能够最大限度的将数据分类，其中越往上的节点的分类效果越好。那么这个分类效果就是一个标准，通过建立这样一个标准，来计算不同特征进行分支选择后的分类情况，找出来最好的那个当成节点，然后在选择下面的节点的时候，继续在剩余的特征中计算每个特征进行分支选择后的分类情况，找出来分类最后的那个当成第二节点，一次类推。

那么这个衡量标准是什么呢？就是熵值

衡量标准：熵

熵：熵是表示随机变量不确定性的度量。简单说就是表示物体内部的混乱程度，例如：在一个手机批发大卖场例如华强北，那么这里面的手机种类肯定多呀，那么手机的种类就混乱呀，但是在华为专卖店里手机的种类就非常稳定了，只有华为，没有三星也没有苹果。

那么这个熵值既然是表示随机变量的不确定性的度量，那么它的计算公式如何呢？

$\begin{array}{r}H(X)=-\sum P_{i}log{P}_i,i=1,2,3...\end{array}$，负号的原因是为了使得计算结果为正，因为$P_i$的取值范围为$[0,1]$,那么$log{P}_i$的取值范围就为$[-\infty ,0]$，加上一个负号就会使得计算结果为正。

例如：集合A和集合B分别是

$A=[1,1,1,1,1,1,1,2,2],B=[1,2,3,4,5,6,7,8,9]$

显然，A,B两个集合都只有9个随机变量，但是A集合总共只有两种类别，而B集合有9种类别，所以A的熵值就会很小，B的熵值就会较大，A要相对稳定一些。

现在通过计算来看一下

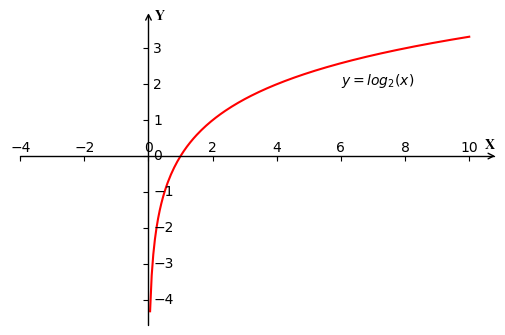
选择$log$的底数为2的原因是在$sklearn$这个库中是用$lo{g}_2$来计算的，实际上，取对数计算的时候只是影响的值的大小，但是并不影响相对大小，也可以选用其他的底数，但是本质上是一样的，而且不同底数之间也可以通过换底公式计算。

$\begin{array}{r}{H}_A(X)=-(\frac{7}{9}\times lo{g}_2\frac{7}{9}+\frac{2}{9}\times lo{g}_2\frac{2}{9})\approx 0.7642\end{array}$

$\begin{array}{r}{H}_B(X)=-(9\times \frac{1}{9}\times lo{g}_2\frac{1}{9})\approx 3.1699\end{array}$

可以看到，A的熵值低于B的熵值，这也证明了集合A比集合B稳定的多。

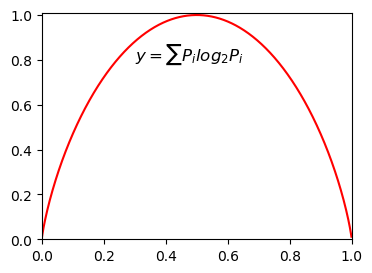
熵：不确定性越大，也就是混乱程度越大，得到的熵值也就越大，当$P=0$或者$P=1$时，$H(P)=0$，此时随机变量完全没有不确定性，因为该事件为不可能事件或者必然事件。当$P=0.5$时候，$H(P)=1$，此时随机变量的不确定性最大。

那么如何决定第一个点的选择呢？

这就引出了信息增益这一概念

信息增益：表示特征X使得类Y的不确定性减少的程度，也就是分类后的专一性，希望分类后的结果是越多的同类在一起，那么这时的混乱程度就降低了也就是熵值降低了，这个降低的程度越大，那么信息增益的程度就越大。

举个栗子：下面是十四天的打球情况

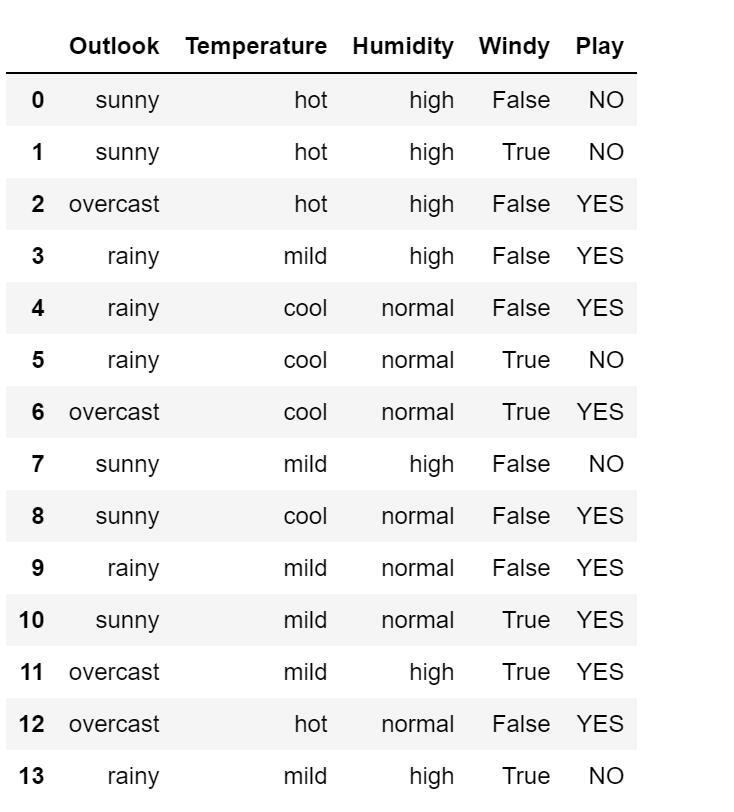
数据：14天的打球情况

特征：4种环境变化Outlook，Temperature，Humidity，Windy，Play

目标：构造决策树

划分的方式有四种如下

• 基于天气的划分

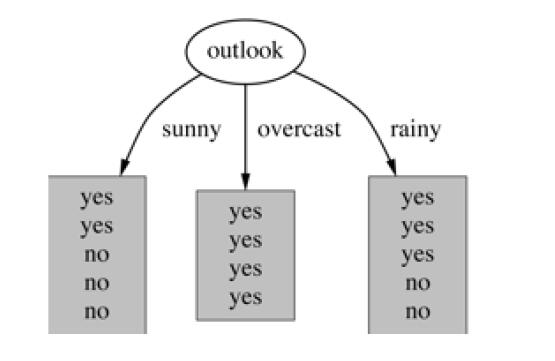
#查看每种天气对应的天数
weathers = ['sunny','overcast','rainy']
days_by_weather = {}
for this_weather in weathers:
    num = np.count_nonzero(data['Outlook'] == this_weather)
    days_by_weather[this_weather] = num
days_by_weather

{'sunny': 5, 'overcast': 4, 'rainy': 5}

• 基于温度的划分

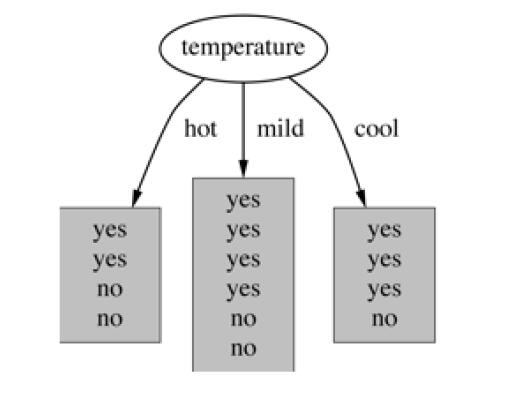
Temperatures = ['hot','cool','mild']
days_by_temperature = {}
for this_Temperature in Temperatures:
    num = np.count_nonzero(data['Temperature'] == this_Temperature)
    days_by_temperature[this_Temperature] = num
days_by_temperature

{'hot': 4, 'cool': 4, 'mild': 6}

• 基于湿度的划分

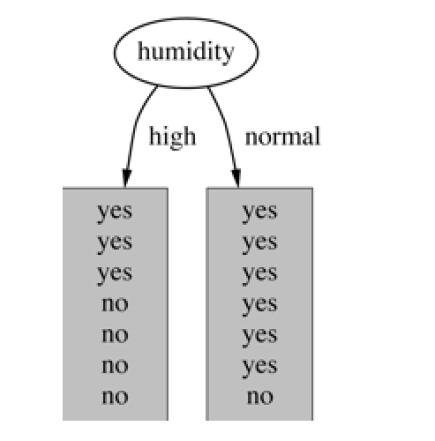
humidities = {'high','normal'}
days_by_humidity = {}
for this_humidity in humidities:
    num = np.count_nonzero(data['Humidity'] == this_humidity)
    days_by_humidity[this_humidity] = num
days_by_humidity

{'high': 7, 'normal': 7}

• 基于有风的划分

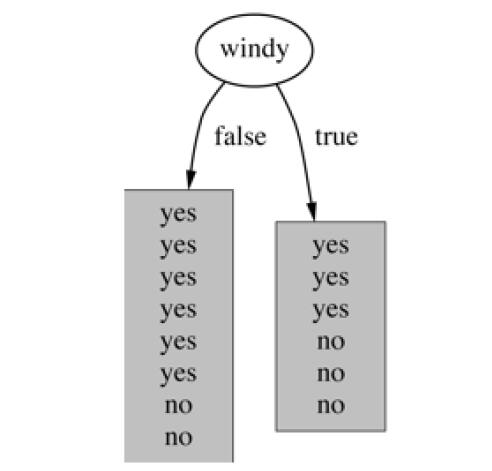
windies = ['NO','YES']
days_by_windies = {}
for this_windy in windies:
    num = np.count_nonzero(data['Windy'] == this_windy)
    days_by_windies[this_windy] = num
days_by_windies

{'NO': 8, 'YES': 6}

在历史数据中查看打球与不打球的天数

plays = ['NO','YES']
days_by_play = {}
for this_play in plays:
    num = np.count_nonzero(data['Play'] == this_play)
    days_by_play[this_play] = num
days_by_play

{'NO': 5, 'YES': 9}

那么此时的熵值为

$\begin{array}{r}-\frac{9}{14}lo{g}_2\frac{9}{14}-\frac{5}{14}lo{g}_2\frac{5}{14}=0.940\end{array}$

然后将上述4个特征注意分析，先从Outlook开始

Outlook = sunny时，计算熵值为$\begin{array}{r}-\frac{3}{5}lo{g}_2\frac{3}{5}-\frac{2}{5}lo{g}_2\frac{2}{5}\end{array}=0.971$

Outlook=overcast时，熵值为0

Outlook = rainy时，熵值为0.971

其余特征分类后的每个子类的熵值计算也是类似

根据统计Outlook取值分别为sunny,overcast,rainy的概率分别为$\begin{array}{r}\frac{5}{14},\frac{4}{14},\frac{5}{14}\end{array}$

那么整体分类后的熵值为，就是分类后的加权熵值为

$\begin{array}{r}\frac{5}{14}\times 0.971+\frac{4}{14}\times 0+\frac{5}{14}\end{array}=0.693$

信息增益：系统的熵值从0.940下降到了0.693，增益为0.247

然后此时来计算信息熵值下降，根据天气、温度、适度，是否有风分类获得的信息增益分别为$0.247,0.029,0.152,0.693$

显然这样的计算得到是第一特征，也就是根节点为天气的时候信息增益最大。

计算信息增益时候的算法叫做ID3算法。但是ID3算法存在一定的问题。今天时间不早了先更新到这里。

最后

以上就是标致时光为你收集整理的决策树算法如何切分特征如何选择节点、信息增益、熵值计算决策树算法的全部内容，希望文章能够帮你解决决策树算法如何切分特征如何选择节点、信息增益、熵值计算决策树算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。