Matlab非线性方程求解

Matlab求解

• 非线性方程求解

最近准备数学竞赛需要对Matlab重新进行一个系统的学习，于是将在学习中学到的东西以博客的形式记录一下，这里介绍的是Matlab中的非线性方程求解

1. 概论

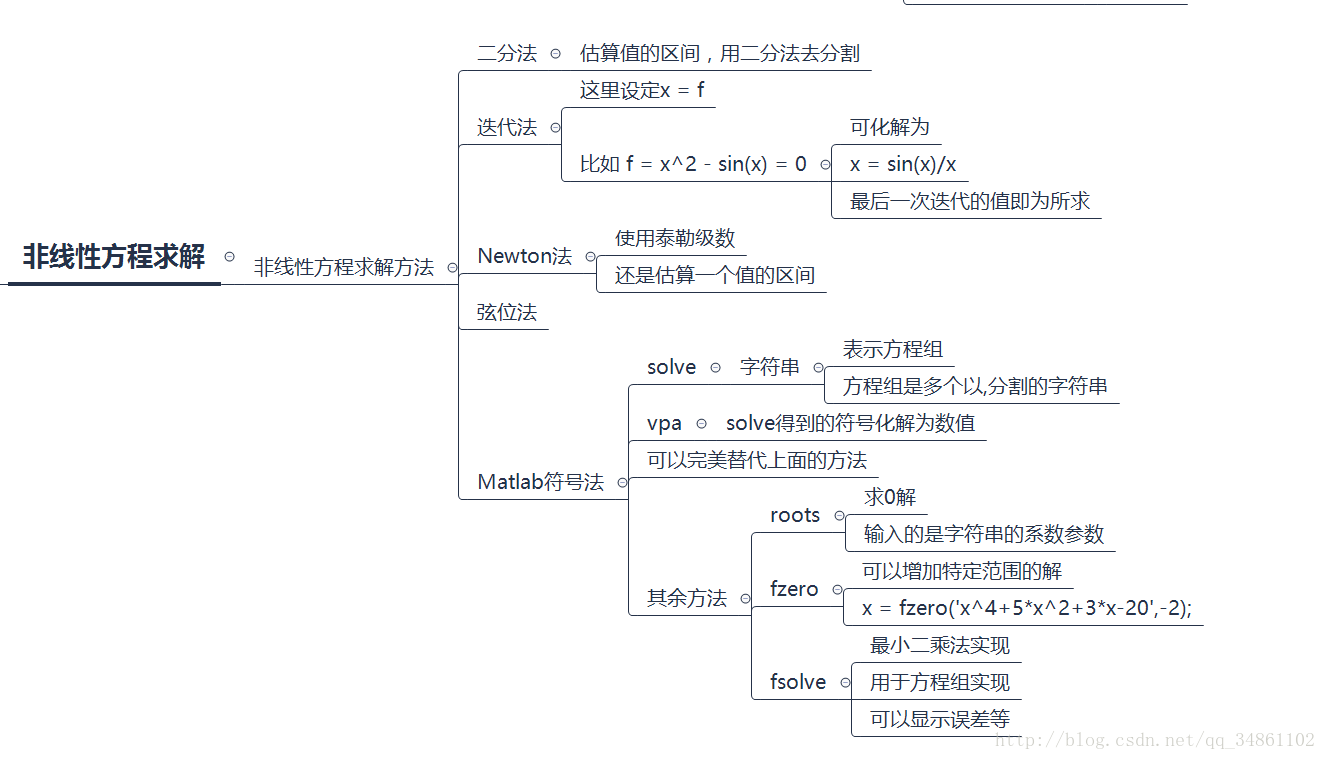
   对Matlab非线性方程求解的概括

   

2. 代码演示

   1. Matlab符号法

      1. fsolve

         
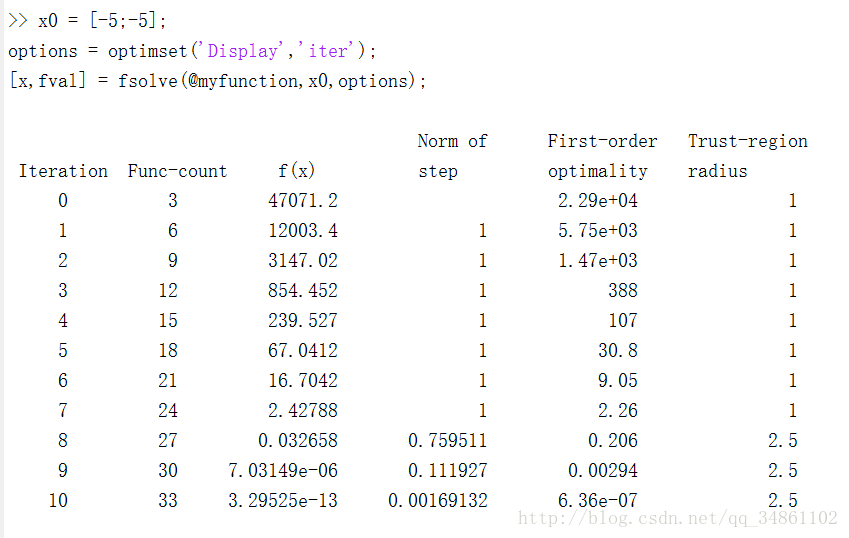
         -x0 = [-5;-5];
options = optimset('Display','iter');
[x,fval] = fsolve(@myfunction,x0,options);
%function F = myfunction(x)
%F = [2*x(1)-x(2)-exp(-x(1));-x(1)+2*x(2)-exp(-x(2))];


      2. fzero

         
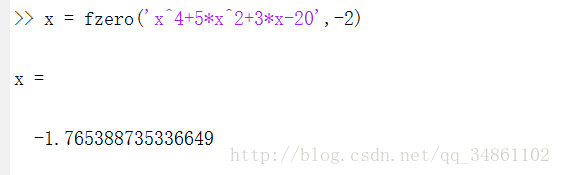
         -x = fzero('x^4+5*x^2+3*x-20',-2);


      3. roots

         
         -[x] = roots([1 0 5 3 -20]);


      4. solve

         
         -%方程组
a = 'x^2 + sqrt(5)*x = -1';
b = 'x + 3*z^2 = 4';
c = 'y*z + 1 = 0';
[u,v,w] = solve(a,b,c);
vpa(u,6)
vpa(v,6)
vpa(w,6)
%方程
[x] = solve('x^3-x-1=0');
vpa(x,6)


   2. Newton法

      
      -newton('f','df',1.2,10^(-6),10)

      这里的newton算法：

      -function [p1,err,k,y] = newton(f,df,p0,delta,max1)
p0,feval(f,p0)
for k = 1:max1
p1 = p0 - feval(f,p0)/feval(df,p0);
err = abs(p1 - p0);
p0 = p1;
p1,err,k,y = feval(f,p1)
if(err<delta)|(y == 0)
break
end
p1,err,k,y = feval(f,p1)
end

      f函数：
      -function y = f(x)
y = x^3 - 3*x + 2;


      df函数：
      -function y = df(x)
y = 3*x^2 - 3;


   3. 迭代法

      迭代算法：
      -function [p0,k,err,p] = fixpt(g,p0,tol,max1)
P(1) = p0;
for k = 2:max1
P(k) = feval(g,P(k-1));
k,err = abs(P(k) - P(k-1))
p = P(k);
if (err < tol)
break;
end;
if k == max1
disp('maximum number of iteration exceeded');
end
end
P


   4. 二分法

      

      二分算法：

      -function [c,err,yc] = bisect(f,a,b,delta)
if nargin < 4 delta = 1e-10;end
ya = feval(f,a);
yb = feval(f,b);
if yb == 0
c = b;
return
end
if ya*yb>0
disp('(a,b)不是有根区间');
return
end
max1 = 1 + round((log(b-a)-log(delta))/log(2));
for k = 1:max1
c = (a+b)/2;
yc = feval(f,c);
if yc == 0
a = c;
b = c;
break;
elseif yb*yc > 0
b = c;
yb = yc;
else
a = c;
ya = c;
end
if(b-a) < delta
break
end
end
k = (a+b)/2;
c = (a+b)/2;
err = abs(b-a);
yc = feval(f,c);


   5. 弦位法

      

      弦位算法：

      -function [p1,err,k,y] = secant(f,p0,p1,delta,max1)
p0,p1,feval(f,p0),feval(f,p1),k=0,
for k = 1:max1
p2 = p1 - feval(f,p1)*(p1-p0)/(feval(f,p1)-feval(f,p0));
err = abs(p2 - p1);
p0 = p1;
p1 = p2;
p1,err,k,y=feval(f,p1)
if(err < delta) | (y == 0)
break
end
end


代码下载地址：http://download.csdn.net/detail/qq_34861102/9922160
原文地址：http://blog.csdn.net/qq_34861102/article/details/76724026

最后

以上就是飞快人生为你收集整理的Matlab非线性方程求解的全部内容，希望文章能够帮你解决Matlab非线性方程求解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。