本文为《数值计算方法》的作业之一
之二:【MATLAB】欧拉法、2阶R-K法、4阶R-K法、预测-校正法(M-S法、A-M法)、有限差分法
解常微分方程之三:
收敛性比较
分别用逐步搜索法、二分法、比例求根法、牛顿法、弦截法求下列方程的根,并分别画出几种方法所求根的收敛速度对比图(即画出相对误差随迭代步数的变化趋势图)
- f ( x ) = c o s ( x ) − x f(x)=cos(x)-x f(x)=cos(x)−x
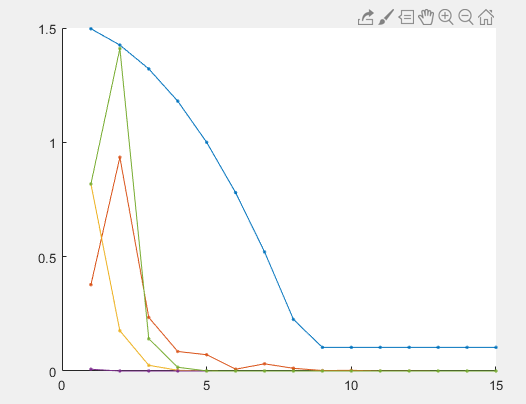
- f ( x ) = x 12 − 1 f(x)=x^{12}-1 f(x)=x12−1
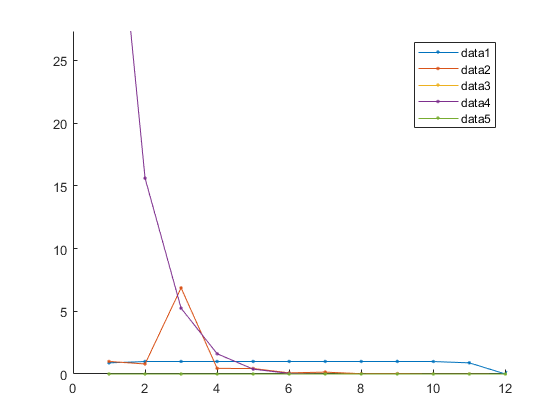
- 代码
clear
% f(x) = 0
f = @(x)cos(x) - x
x_left = -1;
x_right = 2;
stepsMax= 15;
% 逐步搜索法、二分法、比例求根法、牛顿法、弦截法error
errors = zeros(stepsMax,5);
syms x
df = matlabFunction(diff(f(x)))% 求导
if(f(x_left) * f(x_right) >= 0)
disp("f(x_left) * f(x_right) >= 0")
end
% 逐步搜索法
a = x_left;
b = x_right;
h = (x_right - x_left)/stepsMax;
for i = 1:stepsMax
c = a + h;
errors(i,1) = f(c);
if f(c)==0
break;
elseif f(c)*f(b)<0
a = c;
else
b = c;
end
end
% 二分法
a = x_left;
b = x_right;
for i = 1:stepsMax
c = (a+b)/2;
errors(i,2) = f(c);
if f(c)==0
break;
elseif f(c)*f(b)<0
a = c;
else
b = c;
end
end
% 比例求根法
a = x_left;
b = x_right;
for i = 1:stepsMax
c = a - f(a)/(f(a)-f(b))*(a-b);
errors(i,3) = f(c);
if f(c)==0
break;
elseif f(c)*f(b)<0
a = c;
else
b = c;
end
end
% 牛顿法
c = x_right;
for i = 1:stepsMax
c = c - f(c)./df(c);
errors(i,4) = f(c);
if f(c)==0
break;
end
end
% 弦截法
c = x_right;
d = x_left;
for i = 1:stepsMax
temp = d;
d = d - f(d)*(c-d)/(f(c)-f(d));
c = temp;
errors(i,5) = f(d);
if f(c)==0
break;
end
end
figure
hold on
errors = abs(errors);
for i = 1:5
semilogy(errors(:,i),".-");
end
最后
以上就是俭朴荷花最近收集整理的关于【MATLAB】逐步搜索法、二分法、比例求根法、牛顿法、弦截法求方程的根收敛性比较的全部内容,更多相关【MATLAB】逐步搜索法、二分法、比例求根法、牛顿法、弦截法求方程内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复